Éléments hydrauliques parallèles
Storyboard 
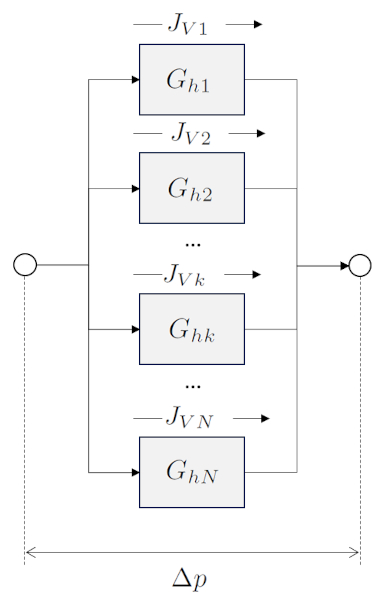
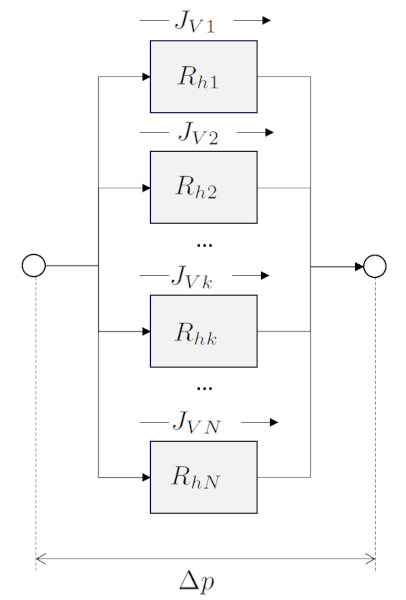
Lorsque les éléments hydrauliques sont connectés en parallèle, le débit est réparti entre eux, tandis que la chute de pression est la même pour tous. La somme des débits individuels donne le débit total, et donc, la résistance hydraulique totale est égale à l'inverse de la somme des inverses des résistances hydrauliques individuelles. En revanche, les conductivités hydrauliques sont additionnées directement.
ID:(1467, 0)
Éléments hydrauliques parallèles
Storyboard 
Lorsque les éléments hydrauliques sont connectés en parallèle, le débit est réparti entre eux, tandis que la chute de pression est la même pour tous. La somme des débits individuels donne le débit total, et donc, la résistance hydraulique totale est égale à l'inverse de la somme des inverses des résistances hydrauliques individuelles. En revanche, les conductivités hydrauliques sont additionnées directement.
Variables
Calculs
Calculs
Équations
Le volumique flux ($J_V$) peut tre calcul partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l' quation suivante :
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
on obtient :
Le volumique flux ($J_V$) peut tre calcul partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l' quation suivante :
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
on obtient :
A conductance hydraulique totale parallèle ($G_{pt}$) combin avec a conductance hydraulique dans un réseau ($G_{hk}$) dans
et associ a resistência hidráulica em uma rede ($R_{hk}$) ainsi qu' l' quation
m ne a résistance hydraulique totale en parallèle ($R_{pt}$) via
Puisque a résistance hydraulique ($R_h$) est gal a conductance hydraulique ($G_h$) conform ment l' quation suivante :
et puisque a conductance hydraulique ($G_h$) est exprim en termes de a viscosité ($\eta$), le rayon du tube ($R$), et le longueur du tube ($\Delta L$) comme suit :
nous pouvons en conclure que :
Avec le flux total ($J_{Vt}$) tant gal le débit volumique dans un réseau ($J_{Vk}$) :
et avec a différence de pression ($\Delta p$) et a conductance hydraulique dans un réseau ($G_{hk}$), ainsi que l' quation
pour chaque l ment, nous en arrivons la conclusion que, avec a conductance hydraulique totale parallèle ($G_{pt}$),
$J_{Vt}=\displaystyle\sum_k J_{Vk} = \displaystyle\sum_k G_{hk}\Delta p = G_{pt}\Delta p$
nous avons
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
nous pouvons introduire a conductance hydraulique ($G_h$), d fini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la mani re suivante :
pour obtenir :
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
nous pouvons introduire a conductance hydraulique ($G_h$), d fini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la mani re suivante :
pour obtenir :
Exemples
Une mani re efficace de mod liser un tube section variable consiste le diviser en sections de rayon constant, puis additionner les r sistances hydrauliques en s rie. Supposons que nous ayons une s rie d' l ments a resistência hidráulica em uma rede ($R_{hk}$), dont la r sistance d pend de a viscosité ($\eta$), le rayon du cylindre k ($R_k$) et le longueur du tube k ($\Delta L_k$), selon l' quation suivante :
Dans chaque l ment, nous consid rons une différence de pression dans un réseau ($\Delta p_k$) ainsi que a resistência hidráulica em uma rede ($R_{hk}$) et le d bit volum trique le volumique flux ($J_V$), en appliquant la loi de Darcy :
La r sistance totale du syst me, le flux volumique total ($J_{Vt}$), est gale la somme des r sistances hydrauliques individuelles ERROR:10133,0 de chaque section :
Ainsi, nous avons :
$J_{Vt}=\displaystyle\sum_k \Delta J_{Vk}=\displaystyle\sum_k \displaystyle\frac{\Delta p_k}{R_{hk}}=\left(\displaystyle\sum_k \displaystyle\frac{1}{R_{hk}}\right)\Delta p\equiv \displaystyle\frac{1}{R_{pt}}J_V$
Par cons quent, le syst me peut tre mod lis comme un conduit unique avec une r sistance hydraulique totale calcul e en additionnant les composants individuels :
Dans le cas d'une somme o les l ments sont connect s en s rie, la conductance hydraulique totale du syst me est calcul e en additionnant les conductances hydrauliques individuelles de chaque l ment.
a résistance hydraulique totale en parallèle ($R_{pt}$), ainsi que a resistência hidráulica em uma rede ($R_{hk}$), dans
et avec a conductance hydraulique dans un réseau ($G_{hk}$) et l' quation
conduit au fait que a conductance hydraulique totale parallèle ($G_{pt}$) peut tre calcul avec
D'abord, les valeurs pour a resistência hidráulica em uma rede ($R_{hk}$) sont calcul es en utilisant les variables a viscosité ($\eta$), le rayon du cylindre k ($R_k$) et le longueur du tube k ($\Delta L_k$) via l' quation suivante :
Ces valeurs sont ensuite additionn es pour obtenir a résistance hydraulique totale en série ($R_{st}$) :
Avec ce r sultat, il est possible de calculer ERROR:6673 pour a résistance hydraulique totale en parallèle ($R_{pt}$) en utilisant :
Une fois ERROR:6673 d termin , le débit volumique dans un réseau ($J_{Vk}$) est calcul via :
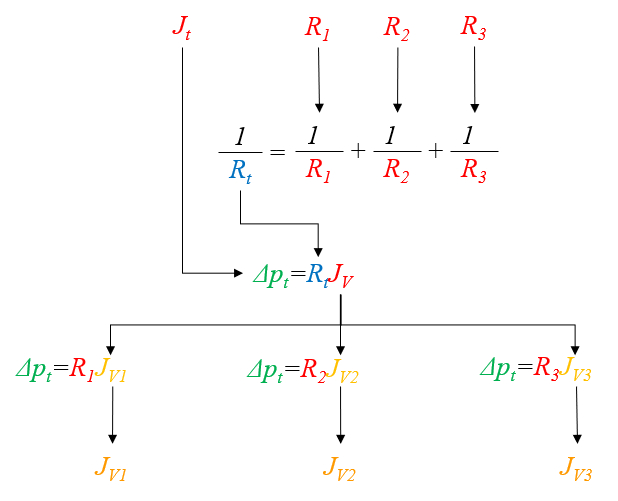
Dans le cas de trois r sistances, les calculs peuvent tre visualis s dans le graphique suivant :
Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons r crire l' quation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) l'aide de l' quation suivante :
Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons r crire l' quation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) l'aide de l' quation suivante :
Avec le rayon du tube ($R$), a viscosité ($\eta$) et le longueur du tube ($\Delta L$) nous avons que une conductance hydraulique ($G_h$) vautxa0:
La somme des couches de sol en parall le, not e le flux total ($J_{Vt}$), est gale la somme de le débit volumique dans un réseau ($J_{Vk}$) :
A conductance hydraulique totale parallèle ($G_{pt}$) est calcul avec la somme de a conductance hydraulique dans un réseau ($G_{hk}$)xa0:
Dans le contexte de la r sistance lectrique, son inverse existe, connu sous le nom de conductance lectrique. De mani re similaire, ce qui serait a conductance hydraulique ($G_h$) peut tre d fini en termes de a résistance hydraulique ($R_h$) travers l'expression :
Dans le contexte de la r sistance lectrique, son inverse existe, connu sous le nom de conductance lectrique. De mani re similaire, ce qui serait a conductance hydraulique ($G_h$) peut tre d fini en termes de a résistance hydraulique ($R_h$) travers l'expression :
Puisque a résistance hydraulique ($R_h$) est gal l'inverse de a conductance hydraulique ($G_h$), il peut tre calcul partir de l'expression de ce dernier. De cette mani re, nous pouvons identifier des param tres li s la g om trie (le longueur du tube ($\Delta L$) et le rayon du tube ($R$)) et au type de liquide (a viscosité ($\eta$)), qui peuvent tre collectivement d sign s sous le nom de une résistance hydraulique ($R_h$) :
A résistance hydraulique totale en parallèle ($R_{pt}$) peut tre calcul comme l'inverse de la somme de a resistência hidráulica em uma rede ($R_{hk}$)xa0:
Darcy r crit l' quation de Hagen Poiseuille de sorte que a différence de pression ($\Delta p$) soit gal a résistance hydraulique ($R_h$) fois le volumique flux ($J_V$)xa0:
Darcy r crit l' quation de Hagen Poiseuille de sorte que a différence de pression ($\Delta p$) soit gal a résistance hydraulique ($R_h$) fois le volumique flux ($J_V$)xa0:
ID:(1467, 0)