Druyd:Knowledge

Elementos hidráulicos paralelos

Storyboard

Quando os elementos hidráulicos estão conectados em paralelo, o fluxo é distribuído entre eles, enquanto a queda de pressão é a mesma para todos. A soma dos fluxos individuais resulta no fluxo total e, portanto, a resistência hidráulica total é igual ao inverso da soma dos inversos das resistências hidráulicas individuais. Por outro lado, as condutividades hidráulicas são somadas diretamente.

>Modelo

ID:(1467, 0)

Mecanismos

Iframe

>Top

Conhecimento

Código

Conceito

Mecanismos

ID:(15726, 0)

Resistência hidráulica de elementos em paralelo

Conceito

>Top

Uma forma eficiente de modelar um tubo com seções transversais variáveis é dividi-lo em seções com raios constantes e, em seguida, somar as resistências hidráulicas em série. Suponhamos que temos uma série de elementos la résistance hydraulique dans un réseau ( $R_{hk}$ ), cuja resistência depende de la viscosidade ( $\eta$ ), o raio do cilindro k ( $R_k$ ) e o comprimento do tubo k ( $\Delta L_k$ ), de acordo com a seguinte equação:

$R_{hk} =\displaystyle\frac{8 \eta | \Delta L_k | }{ \pi R_k ^4}$

Em cada elemento, consideramos uma diferença de pressão em uma rede ( $\Delta p_k$ ) juntamente com la résistance hydraulique dans un réseau ( $R_{hk}$ ) e a taxa de fluxo volumétrico o fluxo de volume ( $J_V$ ), aplicando a lei de Darcy:

$\Delta p = R_h J_V$

A resistência total do sistema, o fluxo de volume total ( $J_{Vt}$ ), será a soma das resistências hidráulicas individuais fluxo de volume em uma rede ( $J_{Vk}$ ) de cada seção:

$J_{Vt} =\displaystyle\sum_k J_{Vk}$

Portanto, temos:

$J_{Vt}=\displaystyle\sum_k \Delta J_{Vk}=\displaystyle\sum_k \displaystyle\frac{\Delta p_k}{R_{hk}}=\left(\displaystyle\sum_k \displaystyle\frac{1}{R_{hk}}\right)\Delta p\equiv \displaystyle\frac{1}{R_{pt}}J_V$

Assim, o sistema pode ser modelado como um único conduto com uma resistência hidráulica total calculada pela soma das componentes individuais:

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

ID:(11068, 0)

Condutância Hidráulica de Elementos Paralelos

Conceito

>Top

No caso de uma soma em que os elementos estão conectados em série, a condutância hidráulica total do sistema é calculada somando as condutâncias hidráulicas individuais de cada elemento.

la resistência hidráulica total em paralelo ( $R_{pt}$ ), juntamente com la résistance hydraulique dans un réseau ( $R_{hk}$ ), em

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

e juntamente com la condutância hidráulica em uma rede ( $G_{hk}$ ) e a equação

$R_{hk} = \displaystyle\frac{1}{ G_{hk} }$

leva ao fato de que la condutância hidráulica total paralela ( $G_{pt}$ ) pode ser calculado com

$G_{pt} =\displaystyle\sum_k G_{hk}$

ID:(15946, 0)

Processo para adição de resistências hidráulicas em paralelo

Descrição

>Top

Primeiramente, calculam-se os valores de la résistance hydraulique dans un réseau ( $R_{hk}$ ) utilizando as variáveis la viscosidade ( $\eta$ ), o raio do cilindro k ( $R_k$ ) e o comprimento do tubo k ( $\Delta L_k$ ) através da seguinte equação:

$R_{hk} =\displaystyle\frac{8 \eta | \Delta L_k | }{ \pi R_k ^4}$

Esses valores são então somados para obter la resistência hidráulica total em série ( $R_{st}$ ):

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

Com esse resultado, é possível calcular ($$) para la resistência hidráulica total em paralelo ( $R_{pt}$ ) usando:

Uma vez determinado ($$), o fluxo de volume em uma rede ( $J_{Vk}$ ) é calculado por meio de:

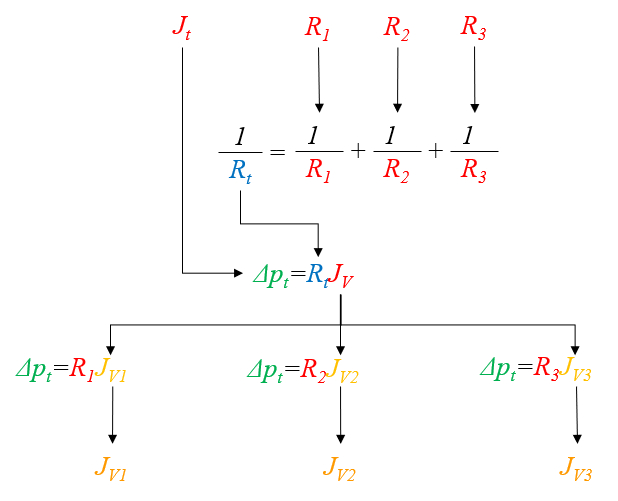
Para o caso de três resistências, os cálculos podem ser visualizados no seguinte gráfico:

ID:(11070, 0)

Modelo

Top

>Top

Parâmetros

Símbolo

Texto

Variáve

Valor

Unidades

Calcular

Valeur MKS

Unidades MKS

$G_{hk}$

G_hk

Condutância hidráulica em uma rede

m^4s/kg

$G_{pt}$

G_pt

Condutância hidráulica total paralela

m^4s/kg

$\pi$

rad

$R_k$

R_k

Raio do cilindro k

$R_{hk}$

R_hk

Résistance hydraulique dans un réseau

kg/m^4s

$R_h$

R_h

Resistência hidráulica

kg/m^4s

$R_{pt}$

R_pt

Resistência hidráulica total em paralelo

kg/m^4s

$\eta$

eta

Viscosidade

Pa s

Variáveis

Símbolo

Texto

Variáve

Valor

Unidades

Calcular

Valeur MKS

Unidades MKS

$\Delta L_k$

DL_k

Comprimento do tubo k

$J_V$

J_V

Fluxo de volume

m^3/s

$J_{Vk}$

J_Vk

Fluxo de volume em uma rede

m^3/s

$J_{Vt}$

J_Vt

Fluxo de volume total

m^3/s

Cálculos

Equação

Primeiro, selecione a equação:

para

, depois, selecione a variável:

para

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve

Dado

Calcular

Objetivo :

Equação

A ser usado

Equações

Equação

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

1/ R_pt =@SUM( 1/ R_hk , k )

$\Delta p = R_h J_V$

Dp = R_h * J_V

$\Delta p = R_h J_V$

Dp = R_h * J_V

$G_{hk} =\displaystyle\frac{ \pi R_k ^4}{8 \eta | \Delta L_k | }$

G_h = pi * R ^4/(8* eta * abs( DL ))

$G_{pt} =\displaystyle\sum_k G_{hk}$

G_pt = @SUM( G_hk , k )

$J_{Vt} = G_{pt} \Delta p$

J_V = G_h * Dp

$J_{Vk} = G_{hk} \Delta p$

J_V = G_h * Dp

$J_{Vt} =\displaystyle\sum_k J_{Vk}$

J_Vt =sum_k J_Vk

$R_{pt} = \displaystyle\frac{1}{ G_{pt} }$

R_h = 1/ G_h

$R_{hk} = \displaystyle\frac{1}{ G_{hk} }$

R_h = 1/ G_h

$R_{hk} =\displaystyle\frac{8 \eta | \Delta L_k | }{ \pi R_k ^4}$

R_h =8* eta * abs( DL )/( pi * R ^4)

ID:(15731, 0)

Lei de Darcy e condutância hidráulica (1)

Equação

>Top, >Modelo

Com a introdução de la condutância hidráulica ( $G_h$ ), podemos reescrever a equação de Hagen-Poiseuille com la diferença de pressão ( $\Delta p$ ) e o fluxo de volume ( $J_V$ ) usando a seguinte equação:

$J_{Vt} = G_{pt} \Delta p$

$J_V = G_h \Delta p$

$G_h$

$G_{pt}$

Condutância hidráulica total paralela

$m^4s/kg$

10136

$J_V$

$J_{Vt}$

Fluxo de volume total

$m^3/s$

6611

Se observarmos a lei de Hagen-Poiseuille, que nos permite calcular o fluxo de volume ( $J_V$ ) a partir de o raio do tubo ( $R$ ), la viscosidade ( $\eta$ ), o comprimento do tubo ( $\Delta L$ ) e la diferença de pressão ( $\Delta p$ ):

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introduzir la condutância hidráulica ( $G_h$ ), definido em termos de o comprimento do tubo ( $\Delta L$ ), o raio do tubo ( $R$ ) e la viscosidade ( $\eta$ ), da seguinte forma:

$G_{hk} =\displaystyle\frac{ \pi R_k ^4}{8 \eta | \Delta L_k | }$

para obter:

$J_V = G_h \Delta p$

ID:(14471, 1)

Lei de Darcy e condutância hidráulica (2)

Equação

>Top, >Modelo

$J_{Vk} = G_{hk} \Delta p$

$J_V = G_h \Delta p$

$G_h$

$G_{hk}$

Condutância hidráulica em uma rede

$m^4s/kg$

10134

$J_V$

$J_{Vk}$

Fluxo de volume em uma rede

$m^3/s$

10133

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introduzir la condutância hidráulica ( $G_h$ ), definido em termos de o comprimento do tubo ( $\Delta L$ ), o raio do tubo ( $R$ ) e la viscosidade ( $\eta$ ), da seguinte forma:

$G_{hk} =\displaystyle\frac{ \pi R_k ^4}{8 \eta | \Delta L_k | }$

para obter:

$J_V = G_h \Delta p$

ID:(14471, 2)

Condutância Hidráulica de um Tubo

Equação

>Top, >Modelo

Com o raio do tubo ( $R$ ), la viscosidade ( $\eta$ ) e o comprimento do tubo ( $\Delta L$ ) temos que uma condutância hidráulica ( $G_h$ ) é:

$G_{hk} =\displaystyle\frac{ \pi R_k ^4}{8 \eta | \Delta L_k | }$

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

$\Delta L$

$\Delta L_k$

Comprimento do tubo k

$m$

10375

$G_h$

$G_{hk}$

Condutância hidráulica em uma rede

$m^4s/kg$

10134

$\pi$

3.1415927

$rad$

5057

$R$

$R_k$

Raio do cilindro k

$m$

10376

$\eta$

Viscosidade

$Pa s$

5422

ID:(15102, 0)

Soma de fluxos paralelos

Equação

>Top, >Modelo

A soma das camadas de solo em paralelo, representada por o fluxo total ( $J_{Vt}$ ), é igual à soma de o fluxo de volume em uma rede ( $J_{Vk}$ ):

$J_{Vt} =\displaystyle\sum_k J_{Vk}$

$J_{Vk}$

Fluxo de volume em uma rede

$m^3/s$

10133

$J_{Vt}$

Fluxo de volume total

$m^3/s$

6611

ID:(4376, 0)

Condutância hidráulica de elementos em paralelo

Equação

>Top, >Modelo

La condutância hidráulica total paralela ( $G_{pt}$ ) é calculado com a soma de la condutância hidráulica em uma rede ( $G_{hk}$ ):

$G_{pt} =\displaystyle\sum_k G_{hk}$

$G_{hk}$

Condutância hidráulica em uma rede

$m^4s/kg$

10134

$G_{pt}$

Condutância hidráulica total paralela

$m^4s/kg$

10136

Com o fluxo total ( $J_{Vt}$ ) sendo igual a o fluxo de volume em uma rede ( $J_{Vk}$ ):

$J_{Vt} =\displaystyle\sum_k J_{Vk}$

e com la diferença de pressão ( $\Delta p$ ) e la condutância hidráulica em uma rede ( $G_{hk}$ ), juntamente com a equação

$J_{Vk} = G_{hk} \Delta p$

para cada elemento, chegamos à conclusão de que, com la condutância hidráulica total paralela ( $G_{pt}$ ),

$J_{Vt}=\displaystyle\sum_k J_{Vk} = \displaystyle\sum_k G_{hk}\Delta p = G_{pt}\Delta p$

temos

$G_{pt} =\displaystyle\sum_k G_{hk}$

ID:(3634, 0)

Condutância hidráulica (1)

Equação

>Top, >Modelo

No contexto da resistência elétrica, existe o seu inverso, conhecido como a condutância elétrica. Da mesma forma, o que seria la condutância hidráulica ( $G_h$ ) pode ser definido em termos de la resistência hidráulica ( $R_h$ ) através da expressão:

$R_{pt} = \displaystyle\frac{1}{ G_{pt} }$

$R_h = \displaystyle\frac{1}{ G_h }$

$G_h$

$G_{pt}$

Condutância hidráulica total paralela

$m^4s/kg$

10136

$R_h$

$R_{pt}$

Resistência hidráulica total em paralelo

$kg/m^4s$

5429

ID:(15092, 1)

Condutância hidráulica (2)

Equação

>Top, >Modelo

$R_{hk} = \displaystyle\frac{1}{ G_{hk} }$

$R_h = \displaystyle\frac{1}{ G_h }$

$G_h$

$G_{hk}$

Condutância hidráulica em uma rede

$m^4s/kg$

10134

$R_h$

$R_{hk}$

Résistance hydraulique dans un réseau

$kg/m^4s$

9887

ID:(15092, 2)

Resistência hidráulica de um tubo

Equação

>Top, >Modelo

Como la resistência hidráulica ( $R_h$ ) é igual ao inverso de la condutância hidráulica ( $G_h$ ), ele pode ser calculado a partir da expressão deste último. Dessa forma, podemos identificar parâmetros relacionados à geometria (o comprimento do tubo ( $\Delta L$ ) e o raio do tubo ( $R$ )) e ao tipo de líquido (la viscosidade ( $\eta$ )), que podem ser denominados coletivamente como uma resistência hidráulica ( $R_h$ ):

$R_{hk} =\displaystyle\frac{8 \eta | \Delta L_k | }{ \pi R_k ^4}$

$R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

$\Delta L$

$\Delta L_k$

Comprimento do tubo k

$m$

10375

$\pi$

3.1415927

$rad$

5057

$R$

$R_k$

Raio do cilindro k

$m$

10376

$R_h$

$R_{hk}$

Résistance hydraulique dans un réseau

$kg/m^4s$

9887

$\eta$

Viscosidade

$Pa s$

5422

Uma vez que la resistência hidráulica ( $R_h$ ) é igual a la condutância hidráulica ( $G_h$ ) conforme a seguinte equação:

$R_h = \displaystyle\frac{1}{ G_h }$

e uma vez que la condutância hidráulica ( $G_h$ ) é expresso em termos de la viscosidade ( $\eta$ ), o raio do tubo ( $R$ ) e o comprimento do tubo ( $\Delta L$ ) da seguinte forma:

$G_{hk} =\displaystyle\frac{ \pi R_k ^4}{8 \eta | \Delta L_k | }$

podemos concluir que:

$R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

ID:(3629, 0)

Resistência hidráulica de elementos paralelos

Equação

>Top, >Modelo

La resistência hidráulica total em paralelo ( $R_{pt}$ ) pode ser calculado como o inverso da soma de la résistance hydraulique dans un réseau ( $R_{hk}$ ):

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

$R_{hk}$

Résistance hydraulique dans un réseau

$kg/m^4s$

9887

$R_{pt}$

Resistência hidráulica total em paralelo

$kg/m^4s$

5429

La condutância hidráulica total paralela ( $G_{pt}$ ) juntamente com la condutância hidráulica em uma rede ( $G_{hk}$ ) em

$G_{pt} =\displaystyle\sum_k G_{hk}$

e, com la résistance hydraulique dans un réseau ( $R_{hk}$ ) e a equação

$R_{hk} = \displaystyle\frac{1}{ G_{hk} }$

leva a la resistência hidráulica total em paralelo ( $R_{pt}$ ) via

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

ID:(3181, 0)

Lei de Darcy e resistência hidráulica (1)

Equação

>Top, >Modelo

Darcy reescreve a equação de Hagen Poiseuille de modo que la diferença de pressão ( $\Delta p$ ) seja igual a la resistência hidráulica ( $R_h$ ) vezes o fluxo de volume ( $J_V$ ):

$\Delta p = R_h J_V$

$J_V$

Fluxo de volume

$m^3/s$

5448

$R_h$

Resistência hidráulica

$kg/m^4s$

5424

O fluxo de volume ( $J_V$ ) pode ser calculado a partir de la condutância hidráulica ( $G_h$ ) e la diferença de pressão ( $\Delta p$ ) usando a seguinte equação:

$J_V = G_h \Delta p$

Além disso, usando a relação para la resistência hidráulica ( $R_h$ ):

$R_h = \displaystyle\frac{1}{ G_h }$

obtém-se o resultado:

$\Delta p = R_h J_V$

ID:(3179, 1)

Lei de Darcy e resistência hidráulica (2)

Equação

>Top, >Modelo

Darcy reescreve a equação de Hagen Poiseuille de modo que la diferença de pressão ( $\Delta p$ ) seja igual a la resistência hidráulica ( $R_h$ ) vezes o fluxo de volume ( $J_V$ ):

$\Delta p = R_h J_V$

$J_V$

Fluxo de volume

$m^3/s$

5448

$R_h$

Resistência hidráulica

$kg/m^4s$

5424

O fluxo de volume ( $J_V$ ) pode ser calculado a partir de la condutância hidráulica ( $G_h$ ) e la diferença de pressão ( $\Delta p$ ) usando a seguinte equação:

$J_V = G_h \Delta p$

Além disso, usando a relação para la resistência hidráulica ( $R_h$ ):

$R_h = \displaystyle\frac{1}{ G_h }$

obtém-se o resultado:

$\Delta p = R_h J_V$

ID:(3179, 2)