Parallel hydraulic elements
Storyboard 
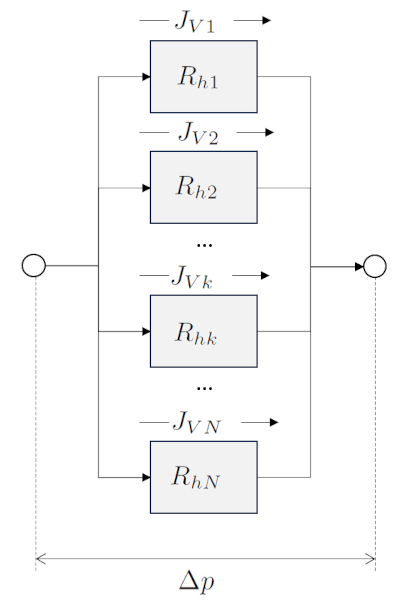
When hydraulic elements are connected in parallel, the flow is distributed among them, while the pressure drop is the same for all of them. The sum of the individual flows results in the total flow, and therefore, the total hydraulic resistance is equal to the inverse of the sum of the inverses of the individual hydraulic resistances. On the other hand, hydraulic conductivities are summed directly.
ID:(1467, 0)
Parallel hydraulic elements
Storyboard 
When hydraulic elements are connected in parallel, the flow is distributed among them, while the pressure drop is the same for all of them. The sum of the individual flows results in the total flow, and therefore, the total hydraulic resistance is equal to the inverse of the sum of the inverses of the individual hydraulic resistances. On the other hand, hydraulic conductivities are summed directly.
Variables
Calculations
Calculations
Equations
The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:
Furthermore, using the relationship for the hydraulic resistance ($R_h$):
results in:
The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:
Furthermore, using the relationship for the hydraulic resistance ($R_h$):
results in:
The parallel total hydraulic conductance ($G_{pt}$) combined with the hydraulic conductance in a network ($G_{hk}$) in
and along with the hydraulic resistance in a network ($R_{hk}$) and the equation
leads to the total hydraulic resistance in parallel ($R_{pt}$) via
Since the hydraulic resistance ($R_h$) is equal to the hydraulic conductance ($G_h$) as per the following equation:
and since the hydraulic conductance ($G_h$) is expressed in terms of the viscosity ($\eta$), the tube radius ($R$), and the tube length ($\Delta L$) as follows:
we can conclude that:
With the total flow ($J_{Vt}$) being equal to the volume flow in a network ($J_{Vk}$):
and with the pressure difference ($\Delta p$) and the hydraulic conductance in a network ($G_{hk}$), along with the equation
for each element, it leads us to the conclusion that with the parallel total hydraulic conductance ($G_{pt}$),
$J_{Vt}=\displaystyle\sum_k J_{Vk} = \displaystyle\sum_k G_{hk}\Delta p = G_{pt}\Delta p$
we have
If we examine the Hagen-Poiseuille law, which allows us to calculate the volume flow ($J_V$) from the tube radius ($R$), the viscosity ($\eta$), the tube length ($\Delta L$), and the pressure difference ($\Delta p$):
we can introduce the hydraulic conductance ($G_h$), defined in terms of the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$), as follows:
to arrive at:
If we examine the Hagen-Poiseuille law, which allows us to calculate the volume flow ($J_V$) from the tube radius ($R$), the viscosity ($\eta$), the tube length ($\Delta L$), and the pressure difference ($\Delta p$):
we can introduce the hydraulic conductance ($G_h$), defined in terms of the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$), as follows:
to arrive at:
Examples
One efficient way to model a tube with varying cross-sections is to divide it into sections with constant radii and then sum the hydraulic resistances in series. Suppose we have a series of elements the hydraulic resistance in a network ($R_{hk}$), whose resistance depends on the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$), according to the following equation:
In each element, we consider a pressure difference in a network ($\Delta p_k$) along with the hydraulic resistance in a network ($R_{hk}$) and the volumetric flow rate the volume flow ($J_V$), where Darcy's law is applied:
The total resistance of the system, the flujo de Volumen Total ($J_{Vt}$), is equal to the sum of the individual hydraulic resistances ERROR:10133,0 of each section:
Thus, we have:
$J_{Vt}=\displaystyle\sum_k \Delta J_{Vk}=\displaystyle\sum_k \displaystyle\frac{\Delta p_k}{R_{hk}}=\left(\displaystyle\sum_k \displaystyle\frac{1}{R_{hk}}\right)\Delta p\equiv \displaystyle\frac{1}{R_{pt}}J_V$
Therefore, the system can be modeled as a single conduit with a total hydraulic resistance calculated by summing the individual components:
In the case of a sum where the elements are connected in series, the total hydraulic conductance of the system is calculated by adding the individual hydraulic conductances of each element.
the total hydraulic resistance in parallel ($R_{pt}$), along with the hydraulic resistance in a network ($R_{hk}$), in
and along with the hydraulic conductance in a network ($G_{hk}$) and the equation
leads to the parallel total hydraulic conductance ($G_{pt}$) can be calculated with:
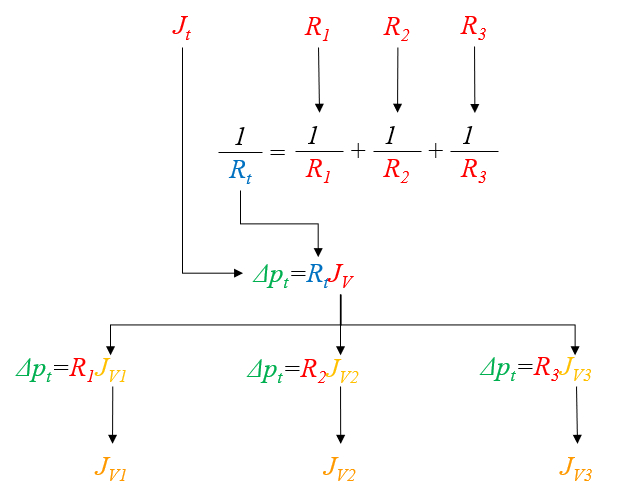
First, values for the hydraulic resistance in a network ($R_{hk}$) are calculated using the variables the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$) through the following equation:
These values are then summed to obtain the total hydraulic resistance in series ($R_{st}$):
With this result, it is possible to calculate the variación de la Presión ($\Delta p$) for the total hydraulic resistance in parallel ($R_{pt}$) using:
Once the variación de la Presión ($\Delta p$) is determined, the volume flow in a network ($J_{Vk}$) is calculated via:
For the case of three resistances, the calculations can be visualized in the following chart:
With the introduction of the hydraulic conductance ($G_h$), we can rewrite the Hagen-Poiseuille equation with the pressure difference ($\Delta p$) and the volume flow ($J_V$) using the following equation:
With the introduction of the hydraulic conductance ($G_h$), we can rewrite the Hagen-Poiseuille equation with the pressure difference ($\Delta p$) and the volume flow ($J_V$) using the following equation:
With the tube radius ($R$), the viscosity ($\eta$) and the tube length ($\Delta L$) we have that a hydraulic conductance ($G_h$) is:
The sum of soil layers in parallel, denoted as the total flow ($J_{Vt}$), is equal to the sum of the volume flow in a network ($J_{Vk}$):
The parallel total hydraulic conductance ($G_{pt}$) is calculated with the sum of the hydraulic conductance in a network ($G_{hk}$):
In the context of electrical resistance, there exists its inverse, known as electrical conductance. Similarly, what would be the hydraulic conductance ($G_h$) can be defined in terms of the hydraulic resistance ($R_h$) through the expression:
In the context of electrical resistance, there exists its inverse, known as electrical conductance. Similarly, what would be the hydraulic conductance ($G_h$) can be defined in terms of the hydraulic resistance ($R_h$) through the expression:
Since the hydraulic resistance ($R_h$) is equal to the inverse of the hydraulic conductance ($G_h$), it can be calculated from the expression of the latter. In this way, we can identify parameters related to geometry (the tube length ($\Delta L$) and the tube radius ($R$)) and the type of liquid (the viscosity ($\eta$)), which can be collectively referred to as a hydraulic resistance ($R_h$):
The total hydraulic resistance in parallel ($R_{pt}$) can be calculated as the inverse of the sum of the hydraulic resistance in a network ($R_{hk}$):
Darcy rewrites the Hagen Poiseuille equation so that the pressure difference ($\Delta p$) is equal to the hydraulic resistance ($R_h$) times the volume flow ($J_V$):
Darcy rewrites the Hagen Poiseuille equation so that the pressure difference ($\Delta p$) is equal to the hydraulic resistance ($R_h$) times the volume flow ($J_V$):
ID:(1467, 0)