Utilisateur:
Eléments hydrauliques en série (3)
Storyboard 
Lorsque les éléments hydrauliques sont connectés en série, le débit reste constant, mais chaque élément hydraulique subit une perte de pression. La somme de ces pertes de pression équivaut à la perte totale, et donc, la résistance hydraulique totale est égale à la somme de toutes les résistances hydrauliques individuelles. En revanche, l'inverse de la conductivité hydraulique totale est égal à la somme des inverses des conductivités hydrauliques.
ID:(2107, 0)
Résistance hydraulique des éléments en série (3)
Concept
Dans le cas d'une somme où les éléments sont connectés en série, la résistance hydraulique totale du système est calculée en additionnant les résistances individuelles de chaque élément.
Une manière de modéliser un tube dont la section varie consiste à le diviser en sections de rayon constant, puis à additionner les résistances hydrauliques en série. Supposons que nous avons une série de a resistência hidráulica em uma rede ($R_{hk}$), qui dépend de a viscosité ($\eta$), le rayon du cylindre k ($R_k$), et le longueur du tube k ($\Delta L_k$) via l'équation suivante :
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
Dans chaque segment, il y aura une différence de pression dans un réseau ($\Delta p_k$) avec a resistência hidráulica em uma rede ($R_{hk}$) et le volumique flux ($J_V$) auxquels la loi de Darcy est appliquée :
| $ \Delta p = R_{h2} J_V $ |
a différence de pression totale ($\Delta p_t$) sera égal à la somme des différence de pression dans un réseau ($\Delta p_k$) individuels :
| $ \Delta p_t =\displaystyle\sum_k \Delta p_k $ |
donc,
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Ainsi, le système peut être modélisé comme un conduit unique avec la résistance hydraulique calculée comme la somme des composantes individuelles :
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
ID:(15954, 0)
Conductance hydraulique des éléments de série (3)
Concept
Dans le cas d'une somme où les éléments sont connectés en série, la conductance hydraulique totale du système est calculée en additionnant les conductances hydrauliques individuelles de chaque élément.
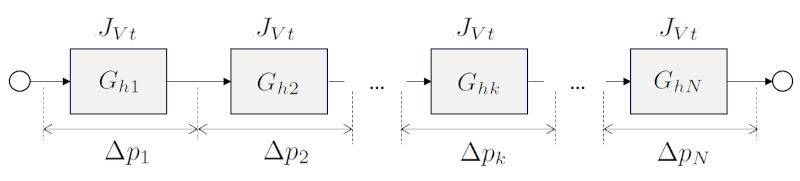
a résistance hydraulique totale en série ($R_{st}$), ainsi que a resistência hidráulica em uma rede ($R_{hk}$), dans
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
et avec a conductance hydraulique dans un réseau ($G_{hk}$) et l'équation
| $ R_{h2} = \displaystyle\frac{1}{ G_{h2} }$ |
conduit au fait que a conductance hydraulique de la série totale ($G_{st}$) peut être calculé avec
| $\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$ |
ID:(15952, 0)
Loi de Darcy et résistance hydraulique (1)
Équation
Darcy réécrit l'équation de Hagen Poiseuille de sorte que a différence de pression ($\Delta p$) soit égal à A résistance hydraulique ($R_h$) fois le volumique flux ($J_V$) :
 $ \Delta p = R_{h1} J_V $ |
 $ \Delta p = R_h J_V $ |
Le volumique flux ($J_V$) peut être calculé à partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l'équation suivante :
| $ J_V = G_h \Delta p $ |
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
on obtient :
| $ \Delta p = R_h J_V $ |
ID:(3179, 1)
Loi de Darcy et résistance hydraulique (2)
Équation
Darcy réécrit l'équation de Hagen Poiseuille de sorte que a différence de pression ($\Delta p$) soit égal à A résistance hydraulique ($R_h$) fois le volumique flux ($J_V$) :
| $ \Delta p = R_{h2} J_V $ |
| $ \Delta p = R_h J_V $ |
Le volumique flux ($J_V$) peut être calculé à partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l'équation suivante :
| $ J_V = G_h \Delta p $ |
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
on obtient :
| $ \Delta p = R_h J_V $ |
ID:(3179, 2)
Loi de Darcy et résistance hydraulique (3)
Équation
Darcy réécrit l'équation de Hagen Poiseuille de sorte que a différence de pression ($\Delta p$) soit égal à A résistance hydraulique ($R_h$) fois le volumique flux ($J_V$) :
| $ \Delta p = R_{h3} J_V $ |
| $ \Delta p = R_h J_V $ |
Le volumique flux ($J_V$) peut être calculé à partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l'équation suivante :
| $ J_V = G_h \Delta p $ |
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
on obtient :
| $ \Delta p = R_h J_V $ |
ID:(3179, 3)
Loi de Darcy et résistance hydraulique (4)
Équation
Darcy réécrit l'équation de Hagen Poiseuille de sorte que a différence de pression ($\Delta p$) soit égal à A résistance hydraulique ($R_h$) fois le volumique flux ($J_V$) :
| $ \Delta p = R_{st} J_V $ |
| $ \Delta p = R_h J_V $ |
Le volumique flux ($J_V$) peut être calculé à partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l'équation suivante :
| $ J_V = G_h \Delta p $ |
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
on obtient :
| $ \Delta p = R_h J_V $ |
ID:(3179, 4)
Loi de Darcy et conductance hydraulique (1)
Équation
Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons réécrire l'équation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) à l'aide de l'équation suivante :
| $ J_V = G_{h1} \Delta p $ |
| $ J_V = G_h \Delta p $ |
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) à partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
nous pouvons introduire a conductance hydraulique ($G_h$), défini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la manière suivante :
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
pour obtenir :
| $ J_V = G_h \Delta p $ |
ID:(14471, 1)
Loi de Darcy et conductance hydraulique (2)
Équation
Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons réécrire l'équation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) à l'aide de l'équation suivante :
| $ J_V = G_{h2} \Delta p $ |
| $ J_V = G_h \Delta p $ |
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) à partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
nous pouvons introduire a conductance hydraulique ($G_h$), défini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la manière suivante :
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
pour obtenir :
| $ J_V = G_h \Delta p $ |
ID:(14471, 2)
Loi de Darcy et conductance hydraulique (3)
Équation
Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons réécrire l'équation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) à l'aide de l'équation suivante :
| $ J_V = G_{h3} \Delta p $ |
| $ J_V = G_h \Delta p $ |
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) à partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
nous pouvons introduire a conductance hydraulique ($G_h$), défini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la manière suivante :
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
pour obtenir :
| $ J_V = G_h \Delta p $ |
ID:(14471, 3)
Loi de Darcy et conductance hydraulique (4)
Équation
Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons réécrire l'équation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) à l'aide de l'équation suivante :
| $ J_V = G_{st} \Delta p $ |
| $ J_V = G_h \Delta p $ |
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) à partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
nous pouvons introduire a conductance hydraulique ($G_h$), défini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la manière suivante :
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
pour obtenir :
| $ J_V = G_h \Delta p $ |
ID:(14471, 4)
Conductance hydraulique (1)
Équation
Dans le contexte de la résistance électrique, son inverse existe, connu sous le nom de conductance électrique. De manière similaire, ce qui serait a conductance hydraulique ($G_h$) peut être défini en termes de a résistance hydraulique ($R_h$) à travers l'expression :
| $ R_{h1} = \displaystyle\frac{1}{ G_{h1} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
.
ID:(15092, 1)
Conductance hydraulique (2)
Équation
Dans le contexte de la résistance électrique, son inverse existe, connu sous le nom de conductance électrique. De manière similaire, ce qui serait a conductance hydraulique ($G_h$) peut être défini en termes de a résistance hydraulique ($R_h$) à travers l'expression :
| $ R_{h2} = \displaystyle\frac{1}{ G_{h2} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
.
ID:(15092, 2)
Conductance hydraulique (3)
Équation
Dans le contexte de la résistance électrique, son inverse existe, connu sous le nom de conductance électrique. De manière similaire, ce qui serait a conductance hydraulique ($G_h$) peut être défini en termes de a résistance hydraulique ($R_h$) à travers l'expression :
| $ R_{h3} = \displaystyle\frac{1}{ G_{h3} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
.
ID:(15092, 3)
Conductance hydraulique (4)
Équation
Dans le contexte de la résistance électrique, son inverse existe, connu sous le nom de conductance électrique. De manière similaire, ce qui serait a conductance hydraulique ($G_h$) peut être défini en termes de a résistance hydraulique ($R_h$) à travers l'expression :
| $ R_{st} = \displaystyle\frac{1}{ G_{st} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
.
ID:(15092, 4)
Somme des résistances en série (3)
Équation
La combinaison en série de a résistance hydraulique 1 ($R_{h1}$), a résistance hydraulique 2 ($R_{h2}$) et a résistance hydraulique 3 ($R_{h3}$) donne une somme totale de a résistance hydraulique totale en série ($R_{st}$) :
| $ R_{st} = R_{h1} + R_{h2} + R_{h3} $ |
ID:(3855, 0)
Différence de pression totale des résistances en série (3)
Équation
Dans les systèmes avec des résistances hydrauliques en série, la pression diminue progressivement à mesure que le fluide traverse chacune d'elles, et la somme de ces chutes de pression est égale à la différence de pression totale sur toute la série.
Dans le cas de trois résistances en série, a résistance hydraulique 1 ($R_{h1}$), a résistance hydraulique 2 ($R_{h2}$) et a résistance hydraulique 3 ($R_{h3}$), avec leurs chutes de pression respectives a différence de pression 1 ($\Delta p_1$), a différence de pression 2 ($\Delta p_2$) et a différence de pression 3 ($\Delta p_3$), la somme de ces chutes est égale à la différence de pression totale a différence de pression totale ($\Delta p_t$) :
| $ \Delta p_t = \Delta p_1 + \Delta p_2 + \Delta p_3 $ |
ID:(12799, 0)
Conductance hydraulique parallèle (3)
Équation
La combinaison en série de a conductance hydraulique 1 ($G_{h1}$), a conductance hydraulique 2 ($G_{h2}$) et a conductance hydraulique 3 ($G_{h3}$) donne une somme totale de a conductance hydraulique de la série totale ($G_{st}$) :
| $\displaystyle\frac{1}{ G_{st} }=\displaystyle\frac{1}{ G_{h1} }+\displaystyle\frac{1}{ G_{h2} }+\displaystyle\frac{1}{ G_{h3} }$ |
ID:(3861, 0)