Benützer:
Hydraulikelemente in Reihe (3)
Storyboard 
Wenn hydraulische Elemente in Serie geschaltet sind, bleibt der Durchfluss konstant, aber in jedem hydraulischen Element tritt ein Druckabfall auf. Die Summe dieser Druckabfälle entspricht dem Gesamtabfall, und daher ist der Gesamthydraulikwiderstand gleich der Summe aller individuellen hydraulischen Widerstände. Andererseits entspricht das Inverse der Gesamthydraulikleitfähigkeit der Summe der Inversen der hydraulischen Leitfähigkeiten.
ID:(2107, 0)
Hydraulischer Widerstand von Elementen in Reihe (3)
Konzept
Im Fall einer Summe, bei der die Elemente in Serie geschaltet sind, wird der Gesamthydraulikwiderstand des Systems berechnet, indem die einzelnen Widerstände jedes Elements addiert werden.
Eine Möglichkeit, ein Rohr mit variierendem Querschnitt zu modellieren, besteht darin, es in Abschnitte mit konstantem Radius zu unterteilen und dann die hydraulischen Widerstände in Serie zu addieren. Nehmen wir an, wir haben eine Serie von die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$), die abhängig von die Viskosität ($\eta$), der Zylinder k Radio ($R_k$) und der Länge des Rohrs k ($\Delta L_k$) durch die folgende Gleichung bestimmt wird:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
In jedem Segment gibt es eine Druckunterschied in einem Netzwerk ($\Delta p_k$) mit die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$) und der Volumenstrom ($J_V$), auf die das Darcysche Gesetz angewendet wird:
| $ \Delta p_2 = R_{h2} J_V $ |
die Gesamtdruckdifferenz ($\Delta p_t$) wird gleich der Summe der einzelnen Druckunterschied in einem Netzwerk ($\Delta p_k$) sein:
| $ \Delta p_t =\displaystyle\sum_k \Delta p_k $ |
daher,
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Somit kann das System als ein einzelner Leiter modelliert werden, dessen hydraulischer Widerstand als Summe der einzelnen Komponenten berechnet wird:
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
ID:(15954, 0)
Hydraulische Leitfähigkeit von Elementen in Reihe (3)
Konzept
Im Fall einer Summe, bei der die Elemente in Serie geschaltet sind, wird die Gesamthydraulikleitfähigkeit des Systems berechnet, indem die individuellen hydraulischen Leitfähigkeiten jedes Elements addiert werden.
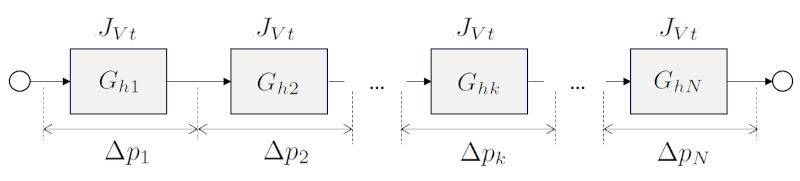
die Insgesamt hydraulischen Widerstand in Serie ($R_{st}$), zusammen mit die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$), in
| $ R_{st} =\displaystyle\sum_k R_{hk} $ |
und zusammen mit die Hydraulische Leitfähigkeit in einem Netzwerk ($G_{hk}$) und der Gleichung
| $ R_{h2} = \displaystyle\frac{1}{ G_{h2} }$ |
führt zu die Gesamte hydraulische Leitfähigkeit der Serie ($G_{st}$) kann berechnet werden mit:
| $\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$ |
ID:(15952, 0)
Darcys Gesetz und hydraulischer Widerstand (1)
Gleichung
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
 $ \Delta p_1 = R_{h1} J_V $ |
 $ \Delta p = R_h J_V $ |
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
| $ J_V = G_h \Delta p $ |
Weiterhin, unter Verwendung der Beziehung für die Hydraulic Resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ergibt sich:
| $ \Delta p = R_h J_V $ |
ID:(3179, 1)
Darcys Gesetz und hydraulischer Widerstand (2)
Gleichung
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
| $ \Delta p_2 = R_{h2} J_V $ |
| $ \Delta p = R_h J_V $ |
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
| $ J_V = G_h \Delta p $ |
Weiterhin, unter Verwendung der Beziehung für die Hydraulic Resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ergibt sich:
| $ \Delta p = R_h J_V $ |
ID:(3179, 2)
Darcys Gesetz und hydraulischer Widerstand (3)
Gleichung
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
| $ \Delta p_3 = R_{h3} J_V $ |
| $ \Delta p = R_h J_V $ |
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
| $ J_V = G_h \Delta p $ |
Weiterhin, unter Verwendung der Beziehung für die Hydraulic Resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ergibt sich:
| $ \Delta p = R_h J_V $ |
ID:(3179, 3)
Darcys Gesetz und hydraulischer Widerstand (4)
Gleichung
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
| $ \Delta p_t = R_{st} J_V $ |
| $ \Delta p = R_h J_V $ |
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
| $ J_V = G_h \Delta p $ |
Weiterhin, unter Verwendung der Beziehung für die Hydraulic Resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ergibt sich:
| $ \Delta p = R_h J_V $ |
ID:(3179, 4)
Darcys Gesetz und hydraulische Leitfähigkeit (1)
Gleichung
Durch die Einführung von die Hydraulische Leitfähigkeit ($G_h$) können wir die Hagen-Poiseuille-Gleichung mit die Druckunterschied ($\Delta p$) und der Volumenstrom ($J_V$) mithilfe der folgenden Gleichung umschreiben:
| $ J_V = G_{h1} \Delta p_1 $ |
| $ J_V = G_h \Delta p $ |
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns ermöglicht, der Volumenstrom ($J_V$) aus der Rohrradius ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
können wir die Hydraulische Leitfähigkeit ($G_h$) einführen, das in Bezug auf der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) definiert ist:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
um zu folgendem Ergebnis zu gelangen:
| $ J_V = G_h \Delta p $ |
ID:(14471, 1)
Darcys Gesetz und hydraulische Leitfähigkeit (2)
Gleichung
Durch die Einführung von die Hydraulische Leitfähigkeit ($G_h$) können wir die Hagen-Poiseuille-Gleichung mit die Druckunterschied ($\Delta p$) und der Volumenstrom ($J_V$) mithilfe der folgenden Gleichung umschreiben:
| $ J_V = G_{h2} \Delta p_2 $ |
| $ J_V = G_h \Delta p $ |
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns ermöglicht, der Volumenstrom ($J_V$) aus der Rohrradius ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
können wir die Hydraulische Leitfähigkeit ($G_h$) einführen, das in Bezug auf der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) definiert ist:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
um zu folgendem Ergebnis zu gelangen:
| $ J_V = G_h \Delta p $ |
ID:(14471, 2)
Darcys Gesetz und hydraulische Leitfähigkeit (3)
Gleichung
Durch die Einführung von die Hydraulische Leitfähigkeit ($G_h$) können wir die Hagen-Poiseuille-Gleichung mit die Druckunterschied ($\Delta p$) und der Volumenstrom ($J_V$) mithilfe der folgenden Gleichung umschreiben:
| $ J_V = G_{h3} \Delta p_3 $ |
| $ J_V = G_h \Delta p $ |
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns ermöglicht, der Volumenstrom ($J_V$) aus der Rohrradius ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
können wir die Hydraulische Leitfähigkeit ($G_h$) einführen, das in Bezug auf der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) definiert ist:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
um zu folgendem Ergebnis zu gelangen:
| $ J_V = G_h \Delta p $ |
ID:(14471, 3)
Darcys Gesetz und hydraulische Leitfähigkeit (4)
Gleichung
Durch die Einführung von die Hydraulische Leitfähigkeit ($G_h$) können wir die Hagen-Poiseuille-Gleichung mit die Druckunterschied ($\Delta p$) und der Volumenstrom ($J_V$) mithilfe der folgenden Gleichung umschreiben:
| $ J_V = G_{st} \Delta p_t $ |
| $ J_V = G_h \Delta p $ |
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns ermöglicht, der Volumenstrom ($J_V$) aus der Rohrradius ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
können wir die Hydraulische Leitfähigkeit ($G_h$) einführen, das in Bezug auf der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) definiert ist:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
um zu folgendem Ergebnis zu gelangen:
| $ J_V = G_h \Delta p $ |
ID:(14471, 4)
Hydraulische Leitfähigkeit (1)
Gleichung
Im Zusammenhang mit dem elektrischen Widerstand gibt es dessen Inverses, das als elektrische Leitfähigkeit bekannt ist. Ebenso kann das, was die Hydraulische Leitfähigkeit ($G_h$) wäre, in Bezug auf die Hydraulic Resistance ($R_h$) durch den Ausdruck definiert werden:
| $ R_{h1} = \displaystyle\frac{1}{ G_{h1} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ID:(15092, 1)
Hydraulische Leitfähigkeit (2)
Gleichung
Im Zusammenhang mit dem elektrischen Widerstand gibt es dessen Inverses, das als elektrische Leitfähigkeit bekannt ist. Ebenso kann das, was die Hydraulische Leitfähigkeit ($G_h$) wäre, in Bezug auf die Hydraulic Resistance ($R_h$) durch den Ausdruck definiert werden:
| $ R_{h2} = \displaystyle\frac{1}{ G_{h2} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ID:(15092, 2)
Hydraulische Leitfähigkeit (3)
Gleichung
Im Zusammenhang mit dem elektrischen Widerstand gibt es dessen Inverses, das als elektrische Leitfähigkeit bekannt ist. Ebenso kann das, was die Hydraulische Leitfähigkeit ($G_h$) wäre, in Bezug auf die Hydraulic Resistance ($R_h$) durch den Ausdruck definiert werden:
| $ R_{h3} = \displaystyle\frac{1}{ G_{h3} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ID:(15092, 3)
Hydraulische Leitfähigkeit (4)
Gleichung
Im Zusammenhang mit dem elektrischen Widerstand gibt es dessen Inverses, das als elektrische Leitfähigkeit bekannt ist. Ebenso kann das, was die Hydraulische Leitfähigkeit ($G_h$) wäre, in Bezug auf die Hydraulic Resistance ($R_h$) durch den Ausdruck definiert werden:
| $ R_{st} = \displaystyle\frac{1}{ G_{st} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ID:(15092, 4)
Summe der Widerstände in Reihe (3)
Gleichung
Die Reihenschaltung von die Hydraulic Resistance 1 ($R_{h1}$), die Hydraulic Resistance 2 ($R_{h2}$) und die Hydraulic Resistance 3 ($R_{h3}$) ergibt eine Gesamtsumme von die Insgesamt hydraulischen Widerstand in Serie ($R_{st}$):
| $ R_{st} = R_{h1} + R_{h2} + R_{h3} $ |
None
ID:(3855, 0)
Gesamtdruckunterschied der Serienwiderstände (3)
Gleichung
In Systemen mit hydraulischen Widerständen in Reihe sinkt der Druck allmählich, während das Fluid durch jeden einzelnen Widerstand fließt, und die Summe dieser Druckabfälle entspricht der gesamten Druckdifferenz über die gesamte Reihe.
Im Fall von drei Widerständen in Reihe, die Hydraulic Resistance 1 ($R_{h1}$), die Hydraulic Resistance 2 ($R_{h2}$) und die Hydraulic Resistance 3 ($R_{h3}$), mit den jeweiligen Druckabfällen die Druckdifferenz 1 ($\Delta p_1$), die Druckdifferenz 2 ($\Delta p_2$) und die Druckdifferenz 3 ($\Delta p_3$), ist die Summe dieser Abfälle gleich der gesamten Druckdifferenz die Gesamtdruckdifferenz ($\Delta p_t$):
| $ \Delta p_t = \Delta p_1 + \Delta p_2 + \Delta p_3 $ |
ID:(12799, 0)
Serie hydraulischer Leitwert (3)
Gleichung
Die Reihenschaltung von die Hydraulische Leitfähigkeit 1 ($G_{h1}$), die Hydraulische Leitfähigkeit 2 ($G_{h2}$) und die Hydraulische Leitfähigkeit 3 ($G_{h3}$) ergibt eine Gesamtsumme von die Gesamte hydraulische Leitfähigkeit der Serie ($G_{st}$):
| $\displaystyle\frac{1}{ G_{st} }=\displaystyle\frac{1}{ G_{h1} }+\displaystyle\frac{1}{ G_{h2} }+\displaystyle\frac{1}{ G_{h3} }$ |
ID:(3861, 0)