Storyboard

Quando os elementos hidráulicos são conectados em série, o fluxo permanece constante, mas cada elemento hidráulico sofre uma queda de pressão. A soma dessas quedas de pressão é igual à queda total, e, portanto, a resistência hidráulica total é igual à soma de todas as resistências hidráulicas individuais. Por outro lado, o inverso da condutividade hidráulica total é igual à soma dos inversos das condutividades hidráulicas.

>Modelo

ID:(2107, 0)

Conceito

>Top

No caso de uma soma em que os elementos estão conectados em série, a resistência hidráulica total do sistema é calculada somando as resistências individuais de cada elemento.

Uma maneira de modelar um tubo com seção variável é dividí-lo em seções de raio constante e, em seguida, somar as resistências hidráulicas em série. Suponhamos que temos uma série de la résistance hydraulique dans un réseau ($R_{hk}$), que depende de la viscosidade ($\eta$), o raio do cilindro k ($R_k$) e o comprimento do tubo k ($\Delta L_k$) através da seguinte equação:

Em cada segmento, haverá Uma diferença de pressão em uma rede ($\Delta p_k$) com la résistance hydraulique dans un réseau ($R_{hk}$) e o fluxo de volume ($J_V$) aos quais a Lei de Darcy é aplicada:

la diferença total de pressão ($\Delta p_t$) será igual à soma das diferença de pressão em uma rede ($\Delta p_k$) individuais:

portanto,

$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$

Assim, o sistema pode ser modelado como um único conduto com a resistência hidráulica calculada como a soma dos componentes individuais:

ID:(15954, 0)

Conceito

>Top

No caso de uma soma em que os elementos estão conectados em série, a condutância hidráulica total do sistema é calculada somando as condutâncias hidráulicas individuais de cada elemento.

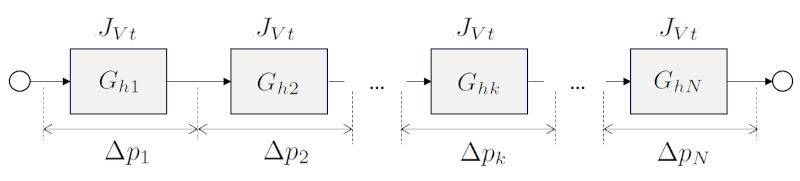
la resistência hidráulica total em série ($R_{st}$), juntamente com la résistance hydraulique dans un réseau ($R_{hk}$), em

e juntamente com la condutância hidráulica em uma rede ($G_{hk}$) e a equação

leva ao fato de que la condutância Hidráulica Série Total ($G_{st}$) pode ser calculado com

ID:(15952, 0)

Equação

>Top, >Modelo

Darcy reescreve a equação de Hagen Poiseuille de modo que la diferença de pressão ($\Delta p$) seja igual a la resistência hidráulica ($R_h$) vezes o fluxo de volume ($J_V$):

$\Delta p = R_{h1} J_V$

$\Delta p = R_h J_V$

Condições

Variáveis

$J_V$

Fluxo de volume

$m^3/s$

5448

$R_h$

$R_{h1}$

Resistência hidráulica 1

$kg/m^4s$

5425

Relação

Desenvolvimento

O fluxo de volume ($J_V$) pode ser calculado a partir de la condutância hidráulica ($G_h$) e la diferença de pressão ($\Delta p$) usando a seguinte equação:

$J_V = G_h \Delta p$

Além disso, usando a relação para la resistência hidráulica ($R_h$):

$R_h = \displaystyle\frac{1}{ G_h }$

obtém-se o resultado:

$\Delta p = R_h J_V$

ID:(3179, 1)

Equação

>Top, >Modelo

Darcy reescreve a equação de Hagen Poiseuille de modo que la diferença de pressão ($\Delta p$) seja igual a la resistência hidráulica ($R_h$) vezes o fluxo de volume ($J_V$):

$\Delta p = R_{h2} J_V$

$\Delta p = R_h J_V$

Condições

Variáveis

$J_V$

Fluxo de volume

$m^3/s$

5448

$R_h$

$R_{h2}$

Resistência hidráulica 2

$kg/m^4s$

5426

Relação

Desenvolvimento

O fluxo de volume ($J_V$) pode ser calculado a partir de la condutância hidráulica ($G_h$) e la diferença de pressão ($\Delta p$) usando a seguinte equação:

$J_V = G_h \Delta p$

Além disso, usando a relação para la resistência hidráulica ($R_h$):

$R_h = \displaystyle\frac{1}{ G_h }$

obtém-se o resultado:

$\Delta p = R_h J_V$

ID:(3179, 2)

Equação

>Top, >Modelo

Darcy reescreve a equação de Hagen Poiseuille de modo que la diferença de pressão ($\Delta p$) seja igual a la resistência hidráulica ($R_h$) vezes o fluxo de volume ($J_V$):

$\Delta p = R_{h3} J_V$

$\Delta p = R_h J_V$

Condições

Variáveis

$J_V$

Fluxo de volume

$m^3/s$

5448

$R_h$

$R_{h3}$

Resistência hidráulica 3

$kg/m^4s$

5427

Relação

Desenvolvimento

O fluxo de volume ($J_V$) pode ser calculado a partir de la condutância hidráulica ($G_h$) e la diferença de pressão ($\Delta p$) usando a seguinte equação:

$J_V = G_h \Delta p$

Além disso, usando a relação para la resistência hidráulica ($R_h$):

$R_h = \displaystyle\frac{1}{ G_h }$

obtém-se o resultado:

$\Delta p = R_h J_V$

ID:(3179, 3)

Equação

>Top, >Modelo

Darcy reescreve a equação de Hagen Poiseuille de modo que la diferença de pressão ($\Delta p$) seja igual a la resistência hidráulica ($R_h$) vezes o fluxo de volume ($J_V$):

$\Delta p = R_{st} J_V$

$\Delta p = R_h J_V$

Condições

Variáveis

$J_V$

Fluxo de volume

$m^3/s$

5448

$R_h$

$R_{st}$

Resistência hidráulica total em série

$kg/m^4s$

5428

Relação

Desenvolvimento

O fluxo de volume ($J_V$) pode ser calculado a partir de la condutância hidráulica ($G_h$) e la diferença de pressão ($\Delta p$) usando a seguinte equação:

$J_V = G_h \Delta p$

Além disso, usando a relação para la resistência hidráulica ($R_h$):

$R_h = \displaystyle\frac{1}{ G_h }$

obtém-se o resultado:

$\Delta p = R_h J_V$

ID:(3179, 4)

Equação

>Top, >Modelo

Com a introdução de la condutância hidráulica ($G_h$), podemos reescrever a equação de Hagen-Poiseuille com la diferença de pressão ($\Delta p$) e o fluxo de volume ($J_V$) usando a seguinte equação:

$J_V = G_{h1} \Delta p$

$J_V = G_h \Delta p$

Condições

Variáveis

$G_h$

$G_{h1}$

Condutância hidráulica 1

$m^4s/kg$

10456

$J_V$

Fluxo de volume

$m^3/s$

5448

Relação

Desenvolvimento

Se observarmos a lei de Hagen-Poiseuille, que nos permite calcular o fluxo de volume ($J_V$) a partir de o raio do tubo ($R$), la viscosidade ($\eta$), o comprimento do tubo ($\Delta L$) e la diferença de pressão ($\Delta p$):

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introduzir la condutância hidráulica ($G_h$), definido em termos de o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$), da seguinte forma:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

para obter:

$J_V = G_h \Delta p$

ID:(14471, 1)

Equação

>Top, >Modelo

Com a introdução de la condutância hidráulica ($G_h$), podemos reescrever a equação de Hagen-Poiseuille com la diferença de pressão ($\Delta p$) e o fluxo de volume ($J_V$) usando a seguinte equação:

$J_V = G_{h2} \Delta p$

$J_V = G_h \Delta p$

Condições

Variáveis

$G_h$

$G_{h2}$

Condutância hidráulica 2

$m^4s/kg$

10457

$J_V$

Fluxo de volume

$m^3/s$

5448

Relação

Desenvolvimento

Se observarmos a lei de Hagen-Poiseuille, que nos permite calcular o fluxo de volume ($J_V$) a partir de o raio do tubo ($R$), la viscosidade ($\eta$), o comprimento do tubo ($\Delta L$) e la diferença de pressão ($\Delta p$):

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introduzir la condutância hidráulica ($G_h$), definido em termos de o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$), da seguinte forma:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

para obter:

$J_V = G_h \Delta p$

ID:(14471, 2)

Equação

>Top, >Modelo

Com a introdução de la condutância hidráulica ($G_h$), podemos reescrever a equação de Hagen-Poiseuille com la diferença de pressão ($\Delta p$) e o fluxo de volume ($J_V$) usando a seguinte equação:

$J_V = G_{h3} \Delta p$

$J_V = G_h \Delta p$

Condições

Variáveis

$G_h$

$G_{h3}$

Condutância hidráulica 3

$m^4s/kg$

10458

$J_V$

Fluxo de volume

$m^3/s$

5448

Relação

Desenvolvimento

Se observarmos a lei de Hagen-Poiseuille, que nos permite calcular o fluxo de volume ($J_V$) a partir de o raio do tubo ($R$), la viscosidade ($\eta$), o comprimento do tubo ($\Delta L$) e la diferença de pressão ($\Delta p$):

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introduzir la condutância hidráulica ($G_h$), definido em termos de o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$), da seguinte forma:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

para obter:

$J_V = G_h \Delta p$

ID:(14471, 3)

Equação

>Top, >Modelo

Com a introdução de la condutância hidráulica ($G_h$), podemos reescrever a equação de Hagen-Poiseuille com la diferença de pressão ($\Delta p$) e o fluxo de volume ($J_V$) usando a seguinte equação:

$J_V = G_{st} \Delta p$

$J_V = G_h \Delta p$

Condições

Variáveis

$G_h$

$G_{st}$

Condutância Hidráulica Série Total

$m^4s/kg$

10135

$J_V$

Fluxo de volume

$m^3/s$

5448

Relação

Desenvolvimento

Se observarmos a lei de Hagen-Poiseuille, que nos permite calcular o fluxo de volume ($J_V$) a partir de o raio do tubo ($R$), la viscosidade ($\eta$), o comprimento do tubo ($\Delta L$) e la diferença de pressão ($\Delta p$):

$J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introduzir la condutância hidráulica ($G_h$), definido em termos de o comprimento do tubo ($\Delta L$), o raio do tubo ($R$) e la viscosidade ($\eta$), da seguinte forma:

$G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

para obter:

$J_V = G_h \Delta p$

ID:(14471, 4)

Equação

>Top, >Modelo

No contexto da resistência elétrica, existe o seu inverso, conhecido como a condutância elétrica. Da mesma forma, o que seria la condutância hidráulica ($G_h$) pode ser definido em termos de la resistência hidráulica ($R_h$) através da expressão:

$R_{h1} = \displaystyle\frac{1}{ G_{h1} }$

$R_h = \displaystyle\frac{1}{ G_h }$

Condições

Variáveis

$G_h$

$G_{h1}$

Condutância hidráulica 1

$m^4s/kg$

10456

$R_h$

$R_{h1}$

Resistência hidráulica 1

$kg/m^4s$

5425

Relação

ID:(15092, 1)

Equação

>Top, >Modelo

No contexto da resistência elétrica, existe o seu inverso, conhecido como a condutância elétrica. Da mesma forma, o que seria la condutância hidráulica ($G_h$) pode ser definido em termos de la resistência hidráulica ($R_h$) através da expressão:

$R_{h2} = \displaystyle\frac{1}{ G_{h2} }$

$R_h = \displaystyle\frac{1}{ G_h }$

Condições

Variáveis

$G_h$

$G_{h2}$

Condutância hidráulica 2

$m^4s/kg$

10457

$R_h$

$R_{h2}$

Resistência hidráulica 2

$kg/m^4s$

5426

Relação

ID:(15092, 2)

Equação

>Top, >Modelo

No contexto da resistência elétrica, existe o seu inverso, conhecido como a condutância elétrica. Da mesma forma, o que seria la condutância hidráulica ($G_h$) pode ser definido em termos de la resistência hidráulica ($R_h$) através da expressão:

$R_{h3} = \displaystyle\frac{1}{ G_{h3} }$

$R_h = \displaystyle\frac{1}{ G_h }$

Condições

Variáveis

$G_h$

$G_{h3}$

Condutância hidráulica 3

$m^4s/kg$

10458

$R_h$

$R_{h3}$

Resistência hidráulica 3

$kg/m^4s$

5427

Relação

ID:(15092, 3)

Equação

>Top, >Modelo

No contexto da resistência elétrica, existe o seu inverso, conhecido como a condutância elétrica. Da mesma forma, o que seria la condutância hidráulica ($G_h$) pode ser definido em termos de la resistência hidráulica ($R_h$) através da expressão:

$R_{st} = \displaystyle\frac{1}{ G_{st} }$

$R_h = \displaystyle\frac{1}{ G_h }$

Condições

Variáveis

$G_h$

$G_{st}$

Condutância Hidráulica Série Total

$m^4s/kg$

10135

$R_h$

$R_{st}$

Resistência hidráulica total em série

$kg/m^4s$

5428

Relação

ID:(15092, 4)

Equação

>Top, >Modelo

A combinação em série de la resistência hidráulica 1 ($R_{h1}$), la resistência hidráulica 2 ($R_{h2}$) e la resistência hidráulica 3 ($R_{h3}$) resulta em uma soma total de la resistência hidráulica total em série ($R_{st}$):

$R_{st} = R_{h1} + R_{h2} + R_{h3}$

Condições

Variáveis

$R_{h1}$

Resistência hidráulica 1

$kg/m^4s$

5425

$R_{h2}$

Resistência hidráulica 2

$kg/m^4s$

5426

$R_{h3}$

Resistência hidráulica 3

$kg/m^4s$

5427

$R_{st}$

Resistência hidráulica total em série

$kg/m^4s$

5428

Relação

ID:(3855, 0)

Equação

>Top, >Modelo

Em sistemas com resistências hidráulicas em série, a pressão diminui progressivamente à medida que o fluido passa por cada uma delas, e a soma dessas quedas de pressão é igual à diferença de pressão total ao longo de toda a série.

No caso de três resistências em série, la resistência hidráulica 1 ($R_{h1}$), la resistência hidráulica 2 ($R_{h2}$) e la resistência hidráulica 3 ($R_{h3}$), com as respectivas quedas de pressão la diferença de pressão 1 ($\Delta p_1$), la diferença de pressão 2 ($\Delta p_2$) e la diferença de pressão 3 ($\Delta p_3$), a soma dessas quedas é igual à diferença de pressão total la diferença total de pressão ($\Delta p_t$):

$\Delta p_t = \Delta p_1 + \Delta p_2 + \Delta p_3$

Condições

Variáveis

$\Delta p_1$

Diferença de pressão 1

$Pa$

9841

$\Delta p_2$

Diferença de pressão 2

$Pa$

5820

$\Delta p_3$

Diferença de pressão 3

$Pa$

5447

$\Delta p_t$

Diferença total de pressão

$Pa$

9842

Relação

ID:(12799, 0)

Equação

>Top, >Modelo

A combinação em série de la condutância hidráulica 1 ($G_{h1}$), la condutância hidráulica 2 ($G_{h2}$) e la condutância hidráulica 3 ($G_{h3}$) resulta em uma soma total de la condutância Hidráulica Série Total ($G_{st}$):

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\frac{1}{ G_{h1} }+\displaystyle\frac{1}{ G_{h2} }+\displaystyle\frac{1}{ G_{h3} }$

Condições

Variáveis

$G_{h1}$

Condutância hidráulica 1

$m^4s/kg$

10456

$G_{h2}$

Condutância hidráulica 2

$m^4s/kg$

10457

$G_{h3}$

Condutância hidráulica 3

$m^4s/kg$

10458

$G_{st}$

Condutância Hidráulica Série Total

$m^4s/kg$

10135

Relação

ID:(3861, 0)