Elementos hidráulicos en serie
Storyboard 
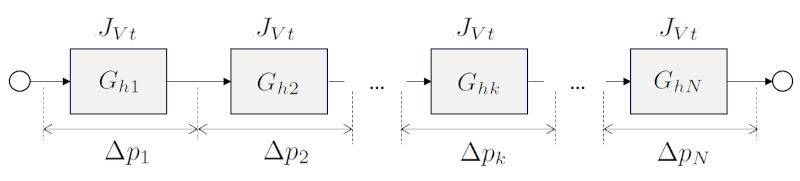
Cuando los elementos hidráulicos se conectan en serie, el flujo permanece constante, pero en cada elemento hidráulico se produce una caída de presión. La suma de estas caídas de presión es igual a la caída total, y, por lo tanto, la resistencia hidráulica total es igual a la suma de todas las resistencias hidráulicas individuales. Por otro lado, el inverso de la conductividad hidráulica total es igual a la suma de los inversos de las conductividades hidráulicas.
ID:(1466, 0)
Elementos hidráulicos en serie
Storyboard 
Cuando los elementos hidráulicos se conectan en serie, el flujo permanece constante, pero en cada elemento hidráulico se produce una caída de presión. La suma de estas caídas de presión es igual a la caída total, y, por lo tanto, la resistencia hidráulica total es igual a la suma de todas las resistencias hidráulicas individuales. Por otro lado, el inverso de la conductividad hidráulica total es igual a la suma de los inversos de las conductividades hidráulicas.
Variables
Cálculos
Cálculos
Ecuaciones
El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:
Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):
se obtiene el resultado final:
El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:
Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):
se obtiene el resultado final:
Una forma de modelar un tubo en el que var a la secci n es dividirlo en secciones de radio constante y luego sumar las resistencias hidr ulicas en serie. Supongamos que tenemos una serie de la resistencia hidráulica en una red ($R_{hk}$), que depende de la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) a trav s de la siguiente ecuaci n:
En cada elemento habr una diferencia de presión en una red ($\Delta p_k$) con la resistencia hidráulica en una red ($R_{hk}$) y el flujo de volumen ($J_V$) para los que se aplica la ley de Darcy
la diferencia de presión total ($\Delta p_t$) ser igual a la suma de las ERROR:10132,0 individuales
por lo que
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Por lo tanto, el sistema se puede modelar como un conducto nico con la resistencia hidr ulica calculada como la suma de las componentes individuales:
Dado que la resistencia hidráulica ($R_h$) es igual a la conductancia hidráulica ($G_h$) seg n la siguiente ecuaci n:
y dado que la conductancia hidráulica ($G_h$) se expresa en t rminos de la viscosidad ($\eta$), el radio del tubo ($R$) y el largo de tubo ($\Delta L$) de la siguiente manera:
podemos concluir que:
La resistencia hidráulica total en serie ($R_{st}$), junto con la resistencia hidráulica en una red ($R_{hk}$) en
y junto con la conductancia hidráulica en una red ($G_{hk}$) y la ecuaci n
conduce a que la conductancia hidráulica total en serie ($G_{st}$) se puede calcular con:
Si observamos la ley de Hagen-Poiseuille, que nos permite calcular el flujo de volumen ($J_V$) a partir de el radio del tubo ($R$), la viscosidad ($\eta$), el largo de tubo ($\Delta L$) y la diferencia de presión ($\Delta p$):
podemos introducir la conductancia hidráulica ($G_h$) definido en t rminos de el largo de tubo ($\Delta L$), el radio del tubo ($R$) y la viscosidad ($\eta$) de la siguiente manera:
y as obtener:
Si observamos la ley de Hagen-Poiseuille, que nos permite calcular el flujo de volumen ($J_V$) a partir de el radio del tubo ($R$), la viscosidad ($\eta$), el largo de tubo ($\Delta L$) y la diferencia de presión ($\Delta p$):
podemos introducir la conductancia hidráulica ($G_h$) definido en t rminos de el largo de tubo ($\Delta L$), el radio del tubo ($R$) y la viscosidad ($\eta$) de la siguiente manera:
y as obtener:
Ejemplos
En el caso de una suma en la que los elementos est n conectados en serie, la resistencia hidr ulica total del sistema se calcula sumando las resistencias individuales de cada elemento.
Una forma de modelar un tubo en el que var a la secci n es dividirlo en secciones de radio constante y luego sumar las resistencias hidr ulicas en serie. Supongamos que tenemos una serie de la resistencia hidráulica en una red ($R_{hk}$), que depende de la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) a trav s de la siguiente ecuaci n:
En cada elemento habr una diferencia de presión en una red ($\Delta p_k$) con la resistencia hidráulica en una red ($R_{hk}$) y el flujo de volumen ($J_V$) para los que se aplica la ley de Darcy
la diferencia de presión total ($\Delta p_t$) ser igual a la suma de las ERROR:10132,0 individuales
por lo que
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Por lo tanto, el sistema se puede modelar como un conducto nico con la resistencia hidr ulica calculada como la suma de las componentes individuales:
En el caso de una suma en la que los elementos est n conectados en serie, la conductancia hidr ulica total del sistema se calcula sumando las conductancias individuales de cada elemento.
la resistencia hidráulica total en serie ($R_{st}$), junto con la resistencia hidráulica en una red ($R_{hk}$) en
y junto con la conductancia hidráulica en una red ($G_{hk}$) y la ecuaci n
conduce a que la conductancia hidráulica total en serie ($G_{st}$) se puede calcular con:
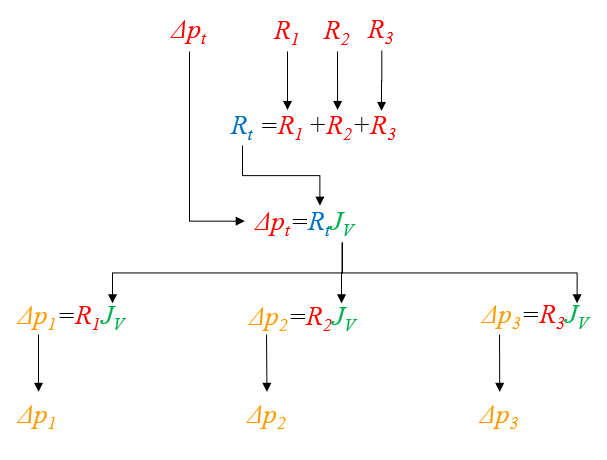
Primero se calculan los valores de la resistencia hidráulica en una red ($R_{hk}$) utilizando la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) mediante la ecuaci n:
Luego se suman para obtener la resistencia hidráulica total en serie ($R_{st}$):
Con este resultado, se puede calcular el flujo de volumen ($J_V$) para la diferencia de presión total ($\Delta p_t$) utilizando:
Una vez obtenido el flujo de volumen ($J_V$), se calcula la diferencia de presión en una red ($\Delta p_k$) mediante:
Para el caso de tres resistencias, el c lculo se puede visualizar en la siguiente gr fica:
Darcy reescribe la ecuaci n de Hagen Poiseuille de modo que la diferencia de presión ($\Delta p$) es igual a la resistencia hidráulica ($R_h$) por el flujo de volumen ($J_V$):
Darcy reescribe la ecuaci n de Hagen Poiseuille de modo que la diferencia de presión ($\Delta p$) es igual a la resistencia hidráulica ($R_h$) por el flujo de volumen ($J_V$):
Dado que la resistencia hidráulica ($R_h$) es igual al inverso de la conductancia hidráulica ($G_h$), podemos calcularlo a partir de la expresi n de este ltimo. De esta manera, podemos identificar par metros relacionados con la geometr a (el largo de tubo ($\Delta L$) y el radio del tubo ($R$)) y el tipo de l quido (la viscosidad ($\eta$)), que pueden ser denominados colectivamente como una resistencia hidráulica ($R_h$):
La diferencia de presión total ($\Delta p_t$) en relaci n a las distintas ERROR:10132,0, lo que nos lleva a la siguiente conclusi n:
Cuando hay varias resistencias hidr ulicas conectadas en serie, podemos calcular la resistencia hidráulica total en serie ($R_{st}$) sumando la resistencia hidráulica en una red ($R_{hk}$), como se expresa en la siguiente f rmula:
En el contexto de la resistencia el ctrica, existe su inverso, conocido como la conductancia el ctrica. De manera an loga, se puede definir lo que ser a la conductancia hidráulica ($G_h$) en funci n de la resistencia hidráulica ($R_h$) mediante la expresi n:
En el contexto de la resistencia el ctrica, existe su inverso, conocido como la conductancia el ctrica. De manera an loga, se puede definir lo que ser a la conductancia hidráulica ($G_h$) en funci n de la resistencia hidráulica ($R_h$) mediante la expresi n:
Con el radio del tubo ($R$), la viscosidad ($\eta$) y el largo de tubo ($\Delta L$) se tiene que una conductancia hidráulica ($G_h$) es:
Con la introducci n de la conductancia hidráulica ($G_h$), podemos reformular la ecuaci n de Hagen-Poiseuille con la diferencia de presión ($\Delta p$) y el flujo de volumen ($J_V$) a trav s de la siguiente ecuaci n:
Con la introducci n de la conductancia hidráulica ($G_h$), podemos reformular la ecuaci n de Hagen-Poiseuille con la diferencia de presión ($\Delta p$) y el flujo de volumen ($J_V$) a trav s de la siguiente ecuaci n:
En el caso de resistencias hidr ulicas en serie, el inverso de la conductancia hidráulica total en serie ($G_{st}$) se calcula sumando los inversos de cada la conductancia hidráulica en una red ($G_{hk}$):
ID:(1466, 0)