Utilizador:
Duas placas com cargas opostas
Storyboard 
A geometria conhecida como placas paralelas pode ser descrita como dois planos infinitos eletricamente carregados com cargas iguais e opostas.
ID:(2076, 0)
Duas placas com cargas opostas
Storyboard
A geometria conhecida como placas paralelas pode ser descrita como dois planos infinitos eletricamente carregados com cargas iguais e opostas.
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
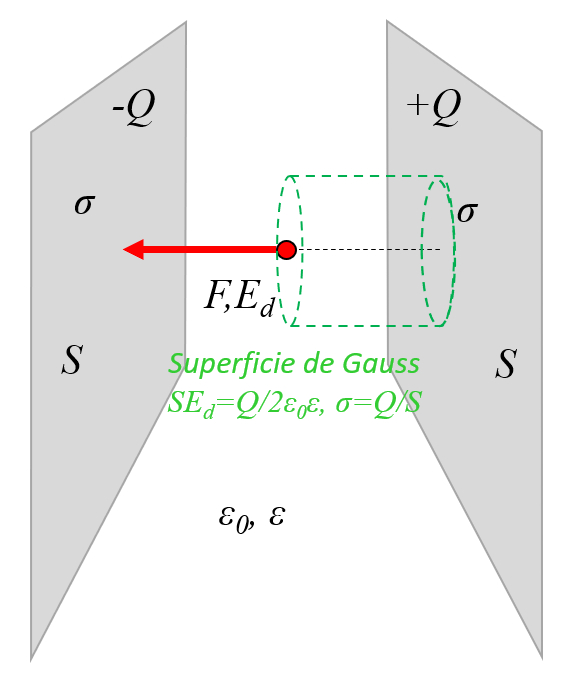
No caso de uma superf cie gaussiana plana, o campo elétrico ($\vec{E}$) constante na dire o de o versor normal para seção ($\hat{n}$). Portanto, utilizando as vari veis la charge ($Q$), la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$), pode-se calcular integrando sobre la superfície na qual o campo elétrico é constante ($dS$):
Al m disso, la densidade de carga por área ($\sigma$) calculado utilizando la superfície ($S$) e la charge ($Q$) de acordo com a seguinte equa o:
Portanto, conclui-se que o campo elétrico, duas placas infinitas ($E_d$) :
O potencial elétrico, duas placas infinitas ($\varphi_d$) em rela o a o campo elétrico, duas placas infinitas ($E_d$) e la posição no eixo z ($z$) expresso como:
De maneira semelhante, o campo elétrico, duas placas infinitas ($E_d$) em rela o a la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la densidade de carga por área ($\sigma$) definido como:
Integrando a partir da origem, obtemos:
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
Portanto, o potencial elétrico, duas placas infinitas ($\varphi_d$) dado por:
O potencial elétrico, duas placas infinitas ($\varphi_d$) em rela o a o campo elétrico, duas placas infinitas ($E_d$) e la posição no eixo z ($z$) expresso como:
De maneira semelhante, o campo elétrico, duas placas infinitas ($E_d$) em rela o a la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la densidade de carga por área ($\sigma$) definido como:
Integrando a partir da origem, obtemos:
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
Portanto, o potencial elétrico, duas placas infinitas ($\varphi_d$) dado por:
Exemplos
No caso de uma superf cie gaussiana plana, o campo elétrico ($\vec{E}$) constante na dire o de o versor normal para seção ($\hat{n}$). Portanto, utilizando as vari veis la charge ($Q$), la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$), pode-se calcular integrando sobre la superfície na qual o campo elétrico é constante ($dS$):
o que mostrado no gr fico
Al m disso, la densidade de carga por área ($\sigma$) calculado utilizando la superfície ($S$) e la charge ($Q$) de acordo com a seguinte equa o:
Portanto, conclui-se que o campo elétrico, duas placas infinitas ($E_d$) :
O potencial elétrico, duas placas infinitas ($\varphi_d$) em rela o a o campo elétrico, duas placas infinitas ($E_d$) e la posição no eixo z ($z$) expresso como:
De maneira semelhante, o campo elétrico, duas placas infinitas ($E_d$) em rela o a la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la densidade de carga por área ($\sigma$) definido como:
Integrando a partir da origem, obtemos:
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
Portanto, o potencial elétrico, duas placas infinitas ($\varphi_d$) dado por:
Como ilustrado no seguinte gr fico:
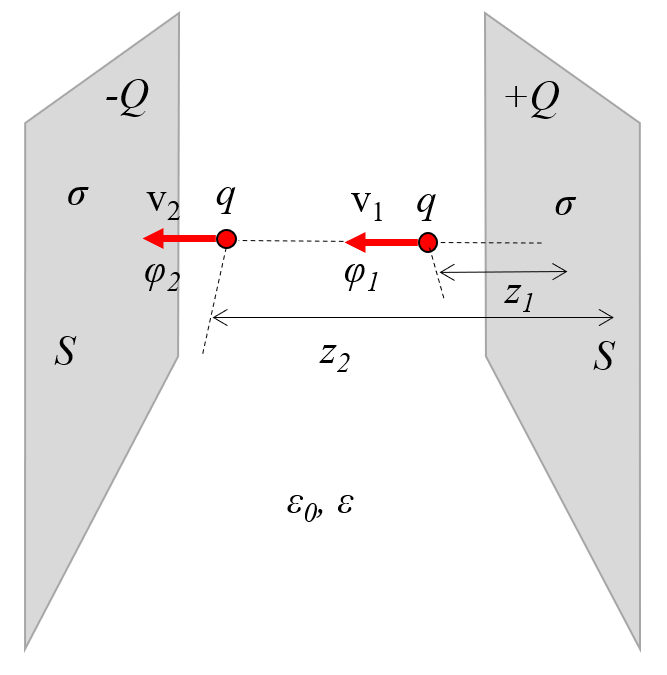
o campo em dois pontos deve possuir a mesma energia. Portanto, as vari veis la charge ($Q$), la massa molar ($m$), la velocidade 1 ($v_1$), la velocidade 2 ($v_2$) e o potencial elétrico 1 ($\varphi_1$) conforme a equa o:
e o potencial elétrico 2 ($\varphi_2$), conforme a equa o:
devem satisfazer a seguinte rela o:
A densidade superficial de carga calculada dividindo a carga total pela rea da superf cie. Portanto, a rela o entre la densidade de carga por área ($\sigma$) e la charge ($Q$) com la zona do condutor ($S$) estabelecida como:
O campo elétrico, duas placas infinitas ($E_d$) com la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la densidade de carga por área ($\sigma$) igual a:
O potencial elétrico, duas placas infinitas ($\varphi_d$) com la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), la densidade de carga por área ($\sigma$) e la posição no eixo z ($z$) igual a:
O potencial elétrico, duas placas infinitas ($\varphi_d$) com la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), la densidade de carga por área ($\sigma$) e la posição no eixo z ($z$) igual a:
Os potenciais el tricos, que representam a energia potencial por unidade de carga, influenciam como a velocidade de uma part cula varia. Consequentemente, devido conserva o de energia entre dois pontos, segue-se que na presen a das vari veis la carga ($q$), la massa molar ($m$), la velocidade 1 ($v_1$), la velocidade 2 ($v_2$), o potencial elétrico 1 ($\varphi_1$) e o potencial elétrico 2 ($\varphi_2$), a seguinte rela o deve ser satisfeita:
ID:(2076, 0)
