Interior de uma esfera isolante
Storyboard 
No caso de uma esfera isolante com distribuição homogênea de carga, as cargas não podem se mover. O campo elétrico pode ser calculado assumindo uma simetria esférica e definindo a superfície de Gauss como uma esfera com um determinado raio. Desta forma, o campo elétrico e o potencial dependerão da carga encerrada por essa superfície.
ID:(2077, 0)
Interior de uma esfera isolante
Storyboard 
No caso de uma esfera isolante com distribuição homogênea de carga, as cargas não podem se mover. O campo elétrico pode ser calculado assumindo uma simetria esférica e definindo a superfície de Gauss como uma esfera com um determinado raio. Desta forma, o campo elétrico e o potencial dependerão da carga encerrada por essa superfície.
Variáveis
Cálculos
Cálculos
Equações
Para o caso de uma superf cie gaussiana esf rica, o campo el trico constante. Portanto, o campo elétrico ($E$) igual a la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la zona do condutor ($S$) conforme:
Dado que a rea da superf cie de la superfície de uma esfera ($S$) igual a o pi ($\pi$) e o raio do disco ($r$), temos:
A carga encerrada na superf cie gaussiana, com la carga encapsulada na superfície gaussiana ($q$), o raio da esfera ($R$) e la distância entre cargas ($r$), dada por:
Portanto, o campo elétrico, esfera, interior ($E_i$) resulta em:
Para o caso de uma superf cie gaussiana esf rica, o campo el trico constante. Portanto, o campo elétrico ($E$) igual a la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la zona do condutor ($S$) conforme:
Dado que a rea da superf cie de la superfície de uma esfera ($S$) igual a o pi ($\pi$) e o raio do disco ($r$), temos:
A carga encerrada na superf cie gaussiana, com la carga encapsulada na superfície gaussiana ($q$), o raio da esfera ($R$) e la distância entre cargas ($r$), dada por:
Portanto, o campo elétrico, esfera, interior ($E_i$) resulta em:
Como a diferen a de potencial o potencial elétrico, esfera isolante, interior ($\varphi_i$) com o campo elétrico, esfera, interior ($E_i$) e o rádio ($r$), obtemos:
Dado que o campo elétrico, esfera, interior ($E_i$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), o raio da esfera ($R$) e la distância entre cargas ($r$) igual a:
Em coordenadas esf ricas, temos:
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
Portanto, o potencial elétrico, esfera isolante, interior ($\varphi_i$) com la distância entre cargas ($r$) resulta em:
Como a diferen a de potencial o potencial elétrico, esfera isolante, interior ($\varphi_i$) com o campo elétrico, esfera, interior ($E_i$) e o rádio ($r$), obtemos:
Dado que o campo elétrico, esfera, interior ($E_i$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), o raio da esfera ($R$) e la distância entre cargas ($r$) igual a:
Em coordenadas esf ricas, temos:
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
Portanto, o potencial elétrico, esfera isolante, interior ($\varphi_i$) com la distância entre cargas ($r$) resulta em:
Exemplos
No caso de uma superf cie gaussiana esf rica, o campo elétrico ($\vec{E}$) constante na dire o de o versor normal para seção ($\hat{n}$). Portanto, utilizando la charge ($Q$), la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$), pode-se calcular integrando sobre la superfície na qual o campo elétrico é constante ($dS$):
Dado que a rea da superf cie de la superfície de uma esfera ($S$) igual a o pi ($\pi$) e o raio do disco ($r$), temos:
o que mostrado no gr fico
la carga encapsulada na superfície gaussiana ($q$) com um raio igual a la distância entre cargas ($r$) e o raio da esfera ($R$) com la charge ($Q$) de modo que:
Para o campo elétrico, esfera, interior ($E_i$), a express o resultante :
Como a diferen a de potencial o potencial elétrico, esfera isolante, interior ($\varphi_i$) com o campo elétrico, esfera, interior ($E_i$) e o rádio ($r$), obtemos:
Dado que o campo elétrico, esfera, interior ($E_i$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), o raio da esfera ($R$) e la distância entre cargas ($r$) igual a:
Em coordenadas esf ricas, temos:
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
Portanto, o potencial elétrico, esfera isolante, interior ($\varphi_i$) com la distância entre cargas ($r$) resulta em:
Como ilustrado no seguinte gr fico:
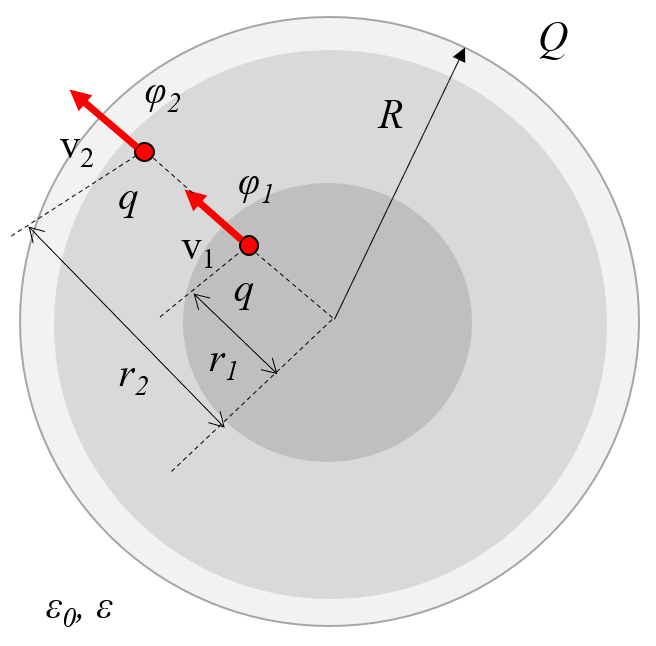
o campo em dois pontos deve possuir a mesma energia. Portanto, as vari veis la charge ($Q$), la massa molar ($m$), la velocidade 1 ($v_1$), la velocidade 2 ($v_2$) e o potencial elétrico 1 ($\varphi_1$) conforme a equa o:
e o potencial elétrico 2 ($\varphi_2$), conforme a equa o:
devem satisfazer a seguinte rela o:
No caso de uma esfera o raio da esfera ($R$) com carga homog nea, a superf cie gaussiana para la distância entre cargas ($r$) inclui la carga encapsulada na superfície gaussiana ($q$) para la charge ($Q$) :
O campo elétrico, esfera, interior ($E_i$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), o raio da esfera ($R$) e la distância entre cargas ($r$) igual a:
No caso de uma esfera o raio da esfera ($R$) com carga homog nea, a superf cie gaussiana para la distância entre cargas ($r$) inclui la carga encapsulada na superfície gaussiana ($q$) para la charge ($Q$) :
O campo elétrico, esfera, interior ($E_i$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), o raio da esfera ($R$) e la distância entre cargas ($r$) igual a:
O potencial elétrico, esfera isolante, interior ($\varphi_i$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), la distância entre cargas ($r$) e o raio da esfera ($R$) igual a:
O potencial elétrico, esfera isolante, interior ($\varphi_i$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), la distância entre cargas ($r$) e o raio da esfera ($R$) igual a:
Os potenciais el tricos, que representam a energia potencial por unidade de carga, influenciam como a velocidade de uma part cula varia. Consequentemente, devido conserva o de energia entre dois pontos, segue-se que na presen a das vari veis la carga ($q$), la massa molar ($m$), la velocidade 1 ($v_1$), la velocidade 2 ($v_2$), o potencial elétrico 1 ($\varphi_1$) e o potencial elétrico 2 ($\varphi_2$), a seguinte rela o deve ser satisfeita:
ID:(2077, 0)