Utilisateur:
Charge ponctuelle
Storyboard 
Une charge ponctuelle est un modèle idéalisé en physique où une charge est concentrée en un seul point sans dimensions. Elle génère un champ électrique qui se propage uniformément vers l'extérieur, diminuant en intensité avec le carré de la distance.
ID:(2074, 0)
Charge ponctuelle
Storyboard
Une charge ponctuelle est un modèle idéalisé en physique où une charge est concentrée en un seul point sans dimensions. Elle génère un champ électrique qui se propage uniformément vers l'extérieur, diminuant en intensité avec le carré de la distance.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
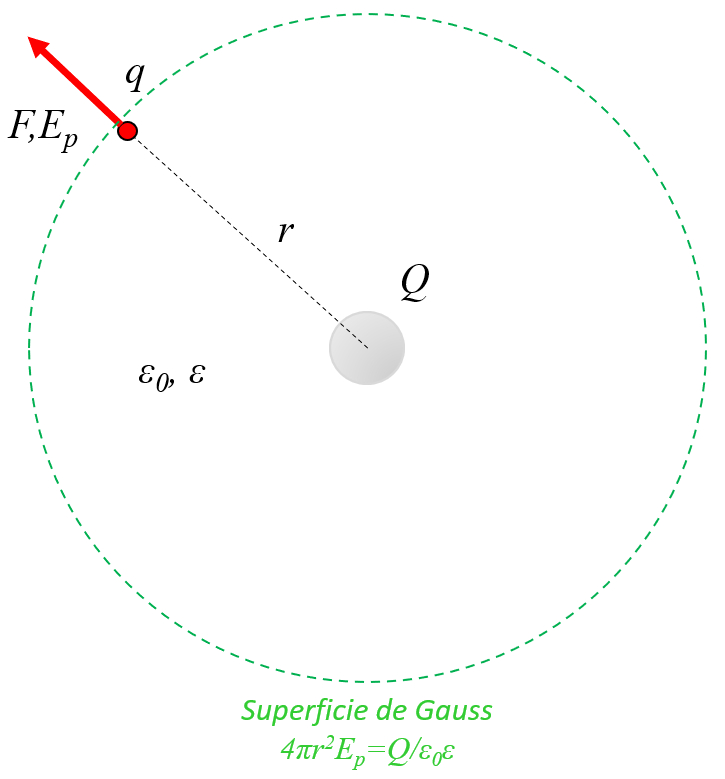
Dans le cas d'une surface gaussienne sph rique, le champ électrique ($\vec{E}$) est constant dans la direction de le versor normal à la section ($\hat{n}$). Par cons quent, en utilisant a charge ($Q$), a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$), on peut calculer en int grant sur a surface sur laquelle le champ électrique est constant ($dS$) :
avec a surface ($S$) pour une sph re de rayon une distance entre les charges ($r$) :
Ainsi, le champ électrique d'une charge ponctuelle ($E_p$) r sulte en :
Dans le cas d'une surface gaussienne sph rique, le champ électrique ($\vec{E}$) est constant dans la direction de le versor normal à la section ($\hat{n}$). Par cons quent, en utilisant a charge ($Q$), a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$), on peut calculer en int grant sur a surface sur laquelle le champ électrique est constant ($dS$) :
avec a surface ($S$) pour une sph re de rayon une distance entre les charges ($r$) :
Ainsi, le champ électrique d'une charge ponctuelle ($E_p$) r sulte en :
Le potentiel électrique, charge ponctuelle ($\varphi_p$) est calcul partir de l'int gration radiale de le champ électrique d'une charge ponctuelle ($E_p$) depuis le radio ($r$) jusqu' l'infini, ce qui donne
D'autre part, pour a charge ($Q$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), la valeur de le champ électrique d'une charge ponctuelle ($E_p$) est
Cela implique qu'en int grant
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
nous obtenons
Le potentiel électrique, charge ponctuelle ($\varphi_p$) est calcul partir de l'int gration radiale de le champ électrique d'une charge ponctuelle ($E_p$) depuis le radio ($r$) jusqu' l'infini, ce qui donne
D'autre part, pour a charge ($Q$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), la valeur de le champ électrique d'une charge ponctuelle ($E_p$) est
Cela implique qu'en int grant
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
nous obtenons
Exemples
Dans le cas d'une surface gaussienne sph rique, le champ électrique ($\vec{E}$) est constant dans la direction de le versor normal à la section ($\hat{n}$). Par cons quent, en utilisant a charge ($Q$), a constante de champ électrique ($\epsilon_0$) et a constante diélectrique ($\epsilon$), on peut calculer en int grant sur a surface sur laquelle le champ électrique est constant ($dS$) :
avec a surface ($S$) pour une sph re de rayon une distance entre les charges ($r$) :
Ainsi, le champ électrique d'une charge ponctuelle ($E_p$) r sulte en :
Le potentiel électrique, charge ponctuelle ($\varphi_p$) est calcul partir de l'int gration radiale de le champ électrique d'une charge ponctuelle ($E_p$) depuis le radio ($r$) jusqu' l'infini, ce qui donne
D'autre part, pour a charge ($Q$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$), la valeur de le champ électrique d'une charge ponctuelle ($E_p$) est
Cela implique qu'en int grant
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
nous obtenons
Comme illustr dans le graphique suivant :
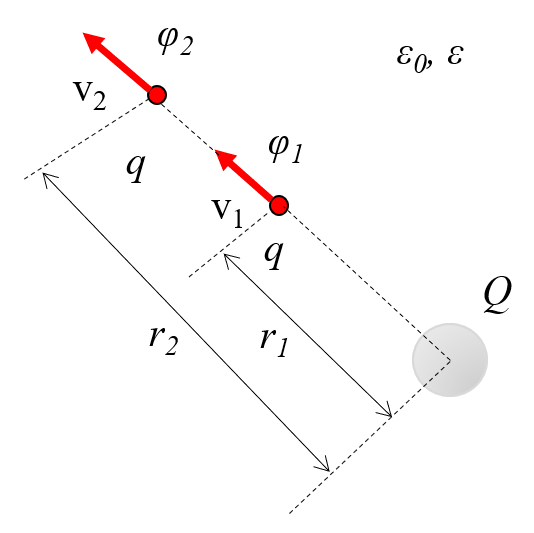
le champ en deux points doit poss der la m me nergie. Par cons quent, les variables a charge ($Q$), a masse molaire ($m$), a vitesse 1 ($v_1$), a vitesse 2 ($v_2$) et le potentiel électrique 1 ($\varphi_1$) selon l' quation :
et le potentiel électrique 2 ($\varphi_2$), selon l' quation :
doivent satisfaire la relation suivante :
Le champ électrique d'une charge ponctuelle ($E_p$) uma fun o de a charge ($Q$), a constante de champ électrique ($\epsilon_0$), a constante diélectrique ($\epsilon$) e a distance entre les charges ($r$) e calculada da seguinte forma:
Le champ électrique d'une charge ponctuelle ($E_p$) uma fun o de a charge ($Q$), a constante de champ électrique ($\epsilon_0$), a constante diélectrique ($\epsilon$) e a distance entre les charges ($r$) e calculada da seguinte forma:
Le potentiel électrique, charge ponctuelle ($\varphi_p$) est avec a charge ($Q$), a distance entre les charges ($r$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$) gal xa0:
Le potentiel électrique, charge ponctuelle ($\varphi_p$) est avec a charge ($Q$), a distance entre les charges ($r$), a constante diélectrique ($\epsilon$) et a constante de champ électrique ($\epsilon_0$) gal xa0:
Les potentiels lectriques, qui repr sentent l' nergie potentielle par unit de charge, influencent la variation de la vitesse d'une particule. Par cons quent, en raison de la conservation de l' nergie entre deux points, il s'ensuit que en pr sence des variables a charge ($q$), a masse molaire ($m$), a vitesse 1 ($v_1$), a vitesse 2 ($v_2$), le potentiel électrique 1 ($\varphi_1$), et le potentiel électrique 2 ($\varphi_2$), la relation suivante doit tre respect e :
ID:(2074, 0)
