Carga puntual
Storyboard 
Una carga puntual es un modelo idealizado en física donde una carga está concentrada en un único punto sin dimensiones. Genera un campo eléctrico que se irradia uniformemente hacia afuera, disminuyendo en intensidad con el cuadrado de la distancia.
ID:(2074, 0)
Carga puntual
Storyboard 
Una carga puntual es un modelo idealizado en física donde una carga está concentrada en un único punto sin dimensiones. Genera un campo eléctrico que se irradia uniformemente hacia afuera, disminuyendo en intensidad con el cuadrado de la distancia.
Variables
Cálculos
Cálculos
Ecuaciones
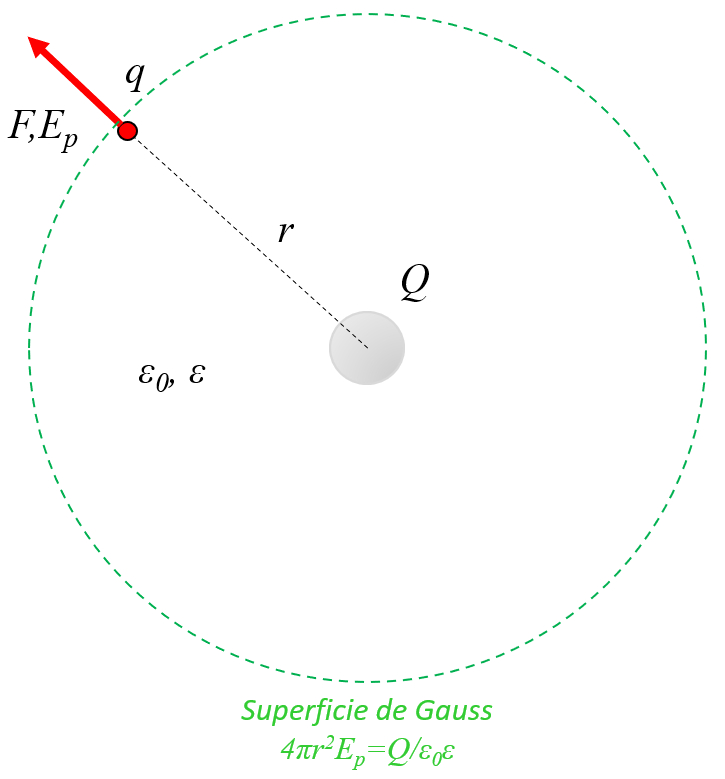
En el caso de una superficie gaussiana esf rica, el campo eléctrico ($\vec{E}$) es constante en la direcci n de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular integrando sobre la superficie en que campo eléctrico es constante ($dS$):
con la superficie ($S$) para una esfera de radio una distancia entre cargas ($r$):
De esta manera, el campo eléctrico de una carga puntual ($E_p$) resulta en:
En el caso de una superficie gaussiana esf rica, el campo eléctrico ($\vec{E}$) es constante en la direcci n de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular integrando sobre la superficie en que campo eléctrico es constante ($dS$):
con la superficie ($S$) para una esfera de radio una distancia entre cargas ($r$):
De esta manera, el campo eléctrico de una carga puntual ($E_p$) resulta en:
El potencial eléctrico, carga puntual ($\varphi_p$) se calcula a partir de la integraci n radial de el campo eléctrico de una carga puntual ($E_p$) desde el radio ($r$) hasta el infinito, lo que resulta en
Por otro lado, para la carga ($Q$), la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$), el valor de el campo eléctrico de una carga puntual ($E_p$) es
Esto implica que al integrar
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
se obtiene
El potencial eléctrico, carga puntual ($\varphi_p$) se calcula a partir de la integraci n radial de el campo eléctrico de una carga puntual ($E_p$) desde el radio ($r$) hasta el infinito, lo que resulta en
Por otro lado, para la carga ($Q$), la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$), el valor de el campo eléctrico de una carga puntual ($E_p$) es
Esto implica que al integrar
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
se obtiene
Ejemplos
En el caso de una superficie gaussiana esf rica, el campo eléctrico ($\vec{E}$) es constante en la direcci n de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular integrando sobre la superficie en que campo eléctrico es constante ($dS$):
con la superficie ($S$) para una esfera de radio una distancia entre cargas ($r$):
De esta manera, el campo eléctrico de una carga puntual ($E_p$) resulta en:
El potencial eléctrico, carga puntual ($\varphi_p$) se calcula a partir de la integraci n radial de el campo eléctrico de una carga puntual ($E_p$) desde el radio ($r$) hasta el infinito, lo que resulta en
Por otro lado, para la carga ($Q$), la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$), el valor de el campo eléctrico de una carga puntual ($E_p$) es
Esto implica que al integrar
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
se obtiene
Como se ilustra en la siguiente gr fica:
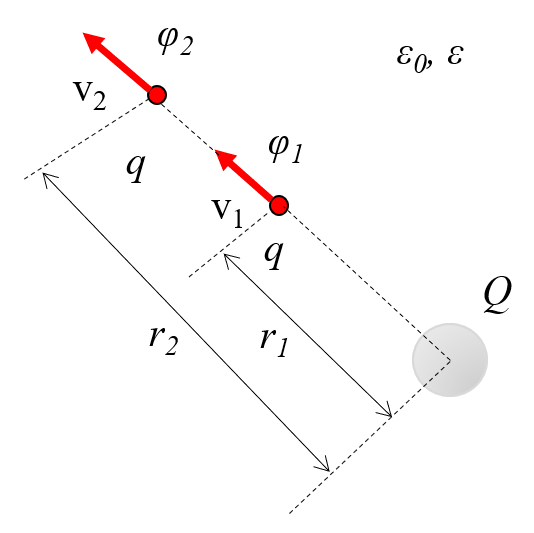
el campo en dos puntos debe poseer la misma energ a. Por lo tanto, las variables la carga ($Q$), la masa de la partícula ($m$), la velocidad 1 ($v_1$), la velocidad 2 ($v_2$), y el potencial eléctrico 1 ($\varphi_1$) seg n la ecuaci n:
y el potencial eléctrico 2 ($\varphi_2$), seg n la ecuaci n:
deben satisfacer la relaci n siguiente:
El campo eléctrico de una carga puntual ($E_p$) es una funci n de la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) y se calcula mediante:
El campo eléctrico de una carga puntual ($E_p$) es una funci n de la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) y se calcula mediante:
El potencial eléctrico, carga puntual ($\varphi_p$) es con la carga ($Q$), la distancia entre cargas ($r$), la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$) igual a:
El potencial eléctrico, carga puntual ($\varphi_p$) es con la carga ($Q$), la distancia entre cargas ($r$), la constante dieléctrica ($\epsilon$) y la constante de campo eléctrico ($\epsilon_0$) igual a:
Los potenciales el ctricos, que representan la energ a potencial por unidad de carga, influyen en c mo var a la velocidad de una part cula. Por consiguiente, la conservaci n de la energ a entre dos puntos implica que, en presencia de las variables la carga ($q$), la masa de la partícula ($m$), la velocidad 1 ($v_1$), la velocidad 2 ($v_2$), el potencial eléctrico 1 ($\varphi_1$) y el potencial eléctrico 2 ($\varphi_2$), se debe cumplir la siguiente relaci n:
ID:(2074, 0)