Usuario:
Exterior de una esfera
Storyboard 
Tanto para una esfera conductora como para una esfera aislante, el campo en su exterior depende únicamente de la carga total, ya sea esta distribuida en la superficie (esfera conductora) o en el interior (esfera aislante).
ID:(2078, 0)
Partícula en campo eléctrico de un esfera, externo
Concepto
En el caso de una superficie gaussiana esférica, el campo eléctrico ($\vec{E}$) es constante en la dirección de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular integrando sobre la superficie en que campo eléctrico es constante ($dS$):
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
Dado que la superficie de la superficie de una esfera ($S$) es igual a el pi ($\pi$) y el radio de un disco ($r$), se tiene:
| $ S = 4 \pi r ^2$ |
lo que se muestra en la grafica
En el exterior de la esfera, el campo eléctrico, esfera, exterior ($E_e$) con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) es igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$ |
Mientras que en el caso de una esfera aislante, el campo eléctrico, esfera, interior ($E_i$) con el radio de la esfera ($R$) es:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
En el caso de que la esfera sea conductora, las cargas se distribuirán sobre la superficie y el campo eléctrico, esfera, interior ($E_i$) será nulo.
ID:(11839, 0)
Partícula en potencial eléctrico de un esfera, externo
Concepto
Como la diferencia de potencial es el potencial eléctrico, esfera, exterior ($\varphi_e$) con el campo eléctrico, esfera, exterior ($E_e$), el campo eléctrico, esfera, interior ($E_i$), el radio de la esfera ($R$) y el radio ($r$), obtenemos:
| $ \varphi_e = - \displaystyle\int_0^ R du\, E_i - \displaystyle\int_ R ^ r du\, E_e $ |
Dado que el campo eléctrico, esfera, exterior ($E_e$) con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) es igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$ |
y que el campo eléctrico, esfera, interior ($E_i$) con el radio interno ($r_i$) es igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
en coordenadas esféricas tenemos:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Por lo tanto, el potencial eléctrico, esfera, exterior ($\varphi_e$) resulta en:
| $ \varphi_2 = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 } $ |
Como se ilustra en la siguiente gráfica:
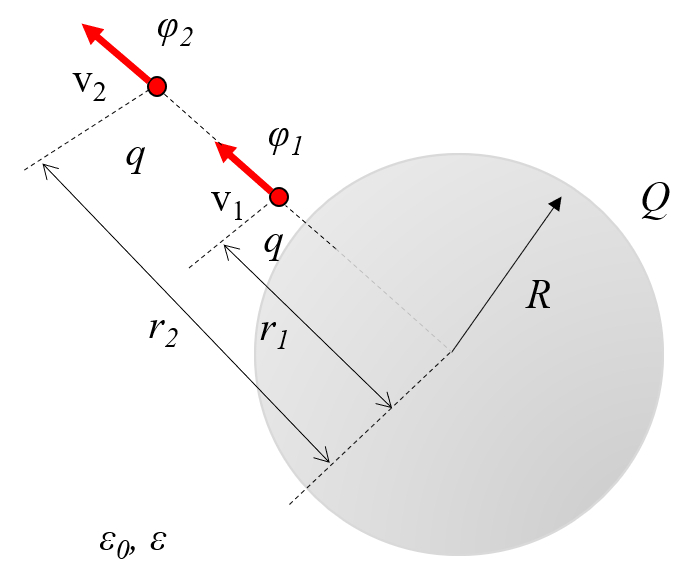
el campo en dos puntos debe poseer la misma energía. Por lo tanto, las variables la carga ($Q$), la masa de la partícula ($m$), la velocidad 1 ($v_1$), la velocidad 2 ($v_2$), y el potencial eléctrico 1 ($\varphi_1$) según la ecuación:
y el potencial eléctrico 2 ($\varphi_2$), según la ecuación:
deben satisfacer la relación siguiente:
| $ \displaystyle\frac{1}{2} m v_1 ^2 + q \varphi_1 = \displaystyle\frac{1}{2} m v_2 ^2 + q \varphi_2 $ |
ID:(11846, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$
E_e = Q /(4 * pi * epsilon_0 * epsilon * r ^2)
$ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$
E_i = Q * r /(4 * pi * epsilon_0 * epsilon * R ^3)
$ \displaystyle\frac{1}{2} m v_1 ^2 + q \varphi_1 = \displaystyle\frac{1}{2} m v_2 ^2 + q \varphi_2 $
m * v_1 ^2/2 + q * phi_1 = m * v_2 ^2/2 + q * phi_2
$ \varphi_2 = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 } $
phi_e =- Q / (4 * pi * epsilon * epsilon_0 * r )
$ \varphi_1 = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r_1 ^2 }{ R ^3 }$
phi_i =- Q * r ^2/(8 * pi * epsilon * epsilon_0 * R ^3)
ID:(15807, 0)
Esfera aislante con carga en todo el volumen, interior
Ecuación
El campo eléctrico, esfera, interior ($E_i$) es con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), el radio de la esfera ($R$) y la distancia entre cargas ($r$) es igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
Para el caso de una superficie gaussiana esférica, el campo es constante y, por lo tanto, el campo eléctrico ($E$) es igual a la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la área del conductor ($S$) según:
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Dado que la superficie de la superficie de una esfera ($S$) es igual a el pi ($\pi$) y el radio de un disco ($r$), se tiene:
| $ S = 4 \pi r ^2$ |
La carga encerrada en la superficie gaussiana, con la carga encapsulada en la superficie de Gauss ($q$), el radio de la esfera ($R$) y la distancia entre cargas ($r$), es:
| $ q =\displaystyle\frac{ r ^3}{ R ^3} Q $ |
Por lo tanto, el campo eléctrico, esfera, interior ($E_i$) resulta en:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
ID:(11447, 0)
Esfera aislante con carga en todo el volumen, exterior
Ecuación
El campo eléctrico, esfera, exterior ($E_e$) es con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) es igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$ |
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
Para el caso de una superficie gausseana esférica el campo es constante por lo que se puede calcular el campo eléctrico ($E$) con la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la área del conductor ($S$) siendo igual a:
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Como la superficie de una esfera ($S$) es con el pi ($\pi$) y el radio de un disco ($r$) igual a:
| $ S = 4 \pi r ^2$ |
el campo eléctrico, esfera, exterior ($E_e$) es con la distancia entre cargas ($r$) igual
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
ID:(11446, 0)
Calculo de potencial eléctrico con geometría esférica, interna
Ecuación
El potencial eléctrico, esfera aislante, interior ($\varphi_i$) es con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), la distancia entre cargas ($r$) y el radio de la esfera ($R$) es igual a:
| $ \varphi_1 = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r_1 ^2 }{ R ^3 }$ |
| $ \varphi_i = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$ |
Como la diferencia de potencial es el potencial eléctrico, esfera aislante, interior ($\varphi_i$) con el campo eléctrico, esfera, interior ($E_i$) y el radio ($r$), obtenemos:
| $ \varphi_i = -\displaystyle\int_0^ r du\, E_i $ |
Dado que el campo eléctrico, esfera, interior ($E_i$) con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), el radio de la esfera ($R$) y la distancia entre cargas ($r$) es igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
en coordenadas esféricas tenemos:
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
Por lo tanto, el potencial eléctrico, esfera aislante, interior ($\varphi_i$) con la distancia entre cargas ($r$) resulta en:
| $ \varphi_i = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$ |
ID:(11583, 0)
Calculo de potencial eléctrico con geometría esférica, externo
Ecuación
El potencial eléctrico, esfera, exterior ($\varphi_e$) es con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) es igual a:
| $ \varphi_2 = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 } $ |
| $ \varphi_e = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r } $ |
Como la diferencia de potencial es el potencial eléctrico, esfera, exterior ($\varphi_e$) con el campo eléctrico, esfera, exterior ($E_e$), el campo eléctrico, esfera, interior ($E_i$), el radio de la esfera ($R$) y el radio ($r$), obtenemos:
| $ \varphi_e = - \displaystyle\int_0^ R du\, E_i - \displaystyle\int_ R ^ r du\, E_e $ |
Dado que el campo eléctrico, esfera, exterior ($E_e$) con el pi ($\pi$), la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la distancia entre cargas ($r$) es igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$ |
y que el campo eléctrico, esfera, interior ($E_i$) con el radio interno ($r_i$) es igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
en coordenadas esféricas tenemos:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Por lo tanto, el potencial eléctrico, esfera, exterior ($\varphi_e$) resulta en:
| $ \varphi_e = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r } $ |
ID:(11584, 0)
Energía de una partícula
Ecuación
Los potenciales eléctricos, que representan la energía potencial por unidad de carga, influyen en cómo varía la velocidad de una partícula. Por consiguiente, la conservación de la energía entre dos puntos implica que, en presencia de las variables la carga ($q$), la masa de la partícula ($m$), la velocidad 1 ($v_1$), la velocidad 2 ($v_2$), el potencial eléctrico 1 ($\varphi_1$) y el potencial eléctrico 2 ($\varphi_2$), se debe cumplir la siguiente relación:
| $ \displaystyle\frac{1}{2} m v_1 ^2 + q \varphi_1 = \displaystyle\frac{1}{2} m v_2 ^2 + q \varphi_2 $ |
ID:(11596, 0)