Benützer:
Thermodynamische Maschinen
Storyboard 
Die thermodynamische Maschine wurde zuerst von Sadi Carnot analysiert, der 1824 in seinen 'Reflections sur la Puissance Matrice du Feu sur les Machines' analysierte, wie Wärme zur Ausführung von Arbeiten verwendet werden kann. Im Prinzip ist es die Anwendung des ersten Hauptsatzes der Thermodynamik, bei dem ein System in einem System Wärme zirkuliert, so dass ein Bruchteil zur Arbeit wird. Der Bruchteil wird als Wirkungsgrad der Maschine bezeichnet und ist nach dem zweiten Hauptsatz der Thermodynamik begrenzt, und die gesamte Wärme kann nicht in Arbeit umgewandelt werden.
ID:(1484, 0)
Arbeiten Sie am vereinfachten Modell
Gleichung
Das Integral im vereinfachten Modell,
| $ W =\displaystyle\oint_C T dS $ |
kann leicht mit der Flächenformel geschätzt werden, indem man die Höhe mit der Basis der Fläche, die die Arbeit repräsentiert, multipliziert:
 $ W = ( T_H - T_C )( S_H - S_C )$ |
ID:(10261, 0)
Arbeiten, um zu investieren
Gleichung
Beim Verkleinern des Volumens von $V_2$ auf $V_1$ muss der Maschine Energie zugeführt werden, dargestellt durch
| $\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$ |
Die Notwendigkeit, diese Energie zuzuführen, spiegelt sich im Vorzeichen des Integrals wider.
ID:(10255, 0)
Gesamtarbeit
Gleichung
Die Gesamtarbeit wird berechnet, indem über den gesamten Zyklus integriert wird, was sowohl den Teil umfasst, in dem Arbeit geleistet wird
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
als auch den Teil, in dem der Prozess umgekehrt wird
| $\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$ |
und somit eine Subtraktion darstellt. Dieser zyklische Prozess wird mathematisch als Integral mit einem Kreis dargestellt und entspricht der Summe der Elemente unter der Kurve in jeder Phase:
| $\displaystyle\oint_C p\,dV=\displaystyle\int_{V_1}^{V_2}p_{dir}\,dV-\displaystyle\int_{V_1}^{V_2}p_{inv}\,dV$ |
ID:(10256, 0)
Grafische Darstellung der erhaltenen Arbeit
Bild
Da die Arbeit
| $ \delta W = p dV $ |
ist, kann sie in einem Druck-Volumen-Diagramm als die Fläche unter der Druckkurve als Funktion des Volumens dargestellt werden:
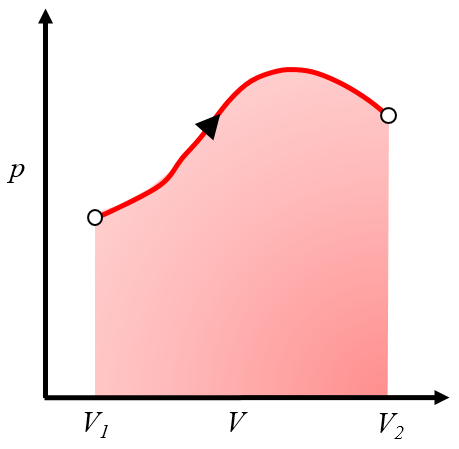
Diese Fläche repräsentiert die erhaltene Arbeit, wenn ein Gas Arbeit leistet, indem es sich vom Volumen $V_1$ auf das Volumen $V_2$ ausdehnt.
Normalerweise wird dieser Prozess durch Erwärmen des Systems erreicht, wodurch es sich ausdehnt und Arbeit leistet. Ein Beispiel wäre ein Kolben mit erhitztem Gas in einem Kessel.
ID:(10266, 0)
Grafische Darstellung der erzielten effektiven Arbeit
Bild
Die erzielte Nettowerk ist die Differenz zwischen der erzielten Arbeit und der erforderlichen Arbeit, um den Zyklus zu vervollständigen:
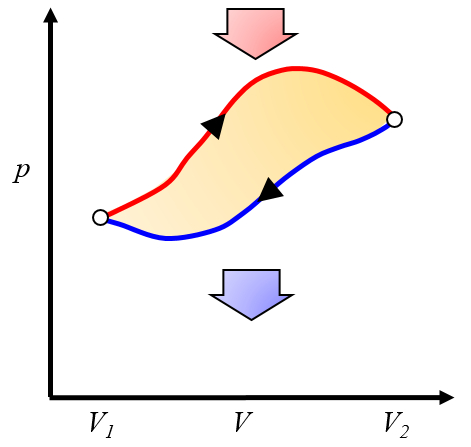
ID:(10268, 0)
Grafische Darstellung der zu investierenden Arbeit
Bild
Um den Prozess wiederholen zu können, muss man vom Volumen $V_2$ auf ein Volumen $V_1$ zurückkehren, was bedeutet, dass man eine Kurve im Druck-Volumen-Diagramm in entgegengesetzter Richtung durchläuft:
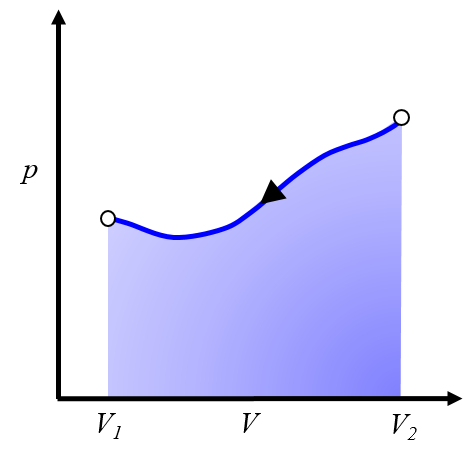
Dies repräsentiert eine aufzubringende Arbeit, die wir leisten müssen, um den Zyklus wiederholen zu können.
Normalerweise wird dieser Prozess durch Abkühlen des Systems erreicht, was zu seiner Kontraktion führt. Die aufzubringende Energie entspricht der dem System entzogenen Wärme.
ID:(10254, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \delta W = p dV $
dW = p * dV
$ W = ( T_H - T_C )( S_H - S_C )$
W =( T_H - T_C )*( S_H - S_C )
$\displaystyle\oint_C p\,dV=\displaystyle\int_{V_1}^{V_2}p_{dir}\,dV-\displaystyle\int_{V_1}^{V_2}p_{inv}\,dV$
int_V1^V2 pdV
$\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$
int_V2^V1 p_inv dV=-int_V1^V2 p_inv dV
ID:(15339, 0)
Arbeit und Druck
Gleichung
Der Differential ungenaue Arbeits ($\delta W$) ist gleich die Druck ($p$) multipliziert mit die Volumenvariation ($dV$):
| $ \delta W = p dV $ |
Da die Mechanische Kraft ($F$) geteilt durch die Abschnitt ($S$) gleich die Druck ($p$) ist:
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
und die Volumenvariation ($dV$) mit der Zurückgelegter Weg ($dx$) gleich ist:
| $ \Delta V = S \Delta s $ |
Die Gleichung für der Differential ungenaue Arbeits ($\delta W$) kann wie folgt ausgedrückt werden:
| $ \delta W = F dx $ |
Daher kann sie geschrieben werden als:
| $ \delta W = p dV $ |
ID:(3468, 0)
Carnot-Zyklus: Schema einer Maschine
Konzept
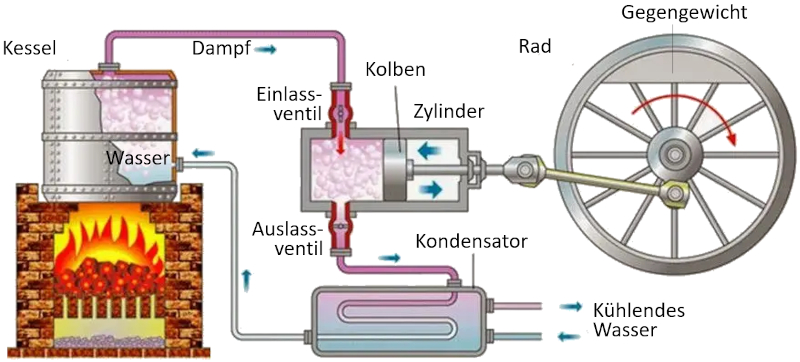
In einer Maschine, die das Konzept von Carnot verwendet, finden folgende Prozesse statt:
• Der Reservoir mit der höheren Temperatur wird mit einem Ofen erzeugt.
• Der Reservoir mit der niedrigeren Temperatur wird durch ein Kühlsystem erzeugt.
• Der aus dem Reservoir erzeugte Dampf expandiert zu einem Gas, wodurch der Kolben verdrängt wird und die Ausgleichsmasse angehoben wird. In der ersten isothermen Phase ist das erste Ventil geöffnet, während das zweite Ventil geschlossen ist. In der zweiten Phase des Prozesses wird das erste Ventil geschlossen, und die Expansion erfolgt adiabatisch.
• In der dritten Phase wird das zweite Ventil geöffnet und mit Hilfe der Ausgleichsmasse wird der Kolben zurückgeführt und das Gas isotherm ausgestoßen. In der vierten Phase wird das Ventil geschlossen, und der Prozess endet adiabatisch.
ID:(11134, 0)
Carnot-Zyklus
Konzept
Sadi Carnot führte [1] das theoretische Konzept der ersten Maschinenkonstruktion ein, die auf einem Temperaturgradienten basierend mechanische Arbeit erzeugen kann. Dies wird durch einen Prozess im Druck-Volumen-Raum erreicht, bei dem Wärme hinzugefügt und extrahiert wird, wie in der Abbildung dargestellt:
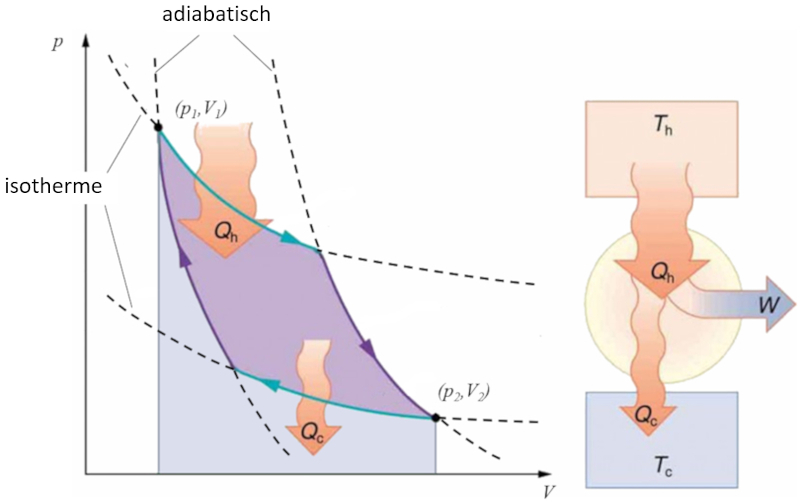
Die Fläche unter der Kurve der Wärme zugeführt ($Q_H$), die von 1 bis 2 reicht, repräsentiert die erforderliche Energiezufuhr, um vom Zustand ($p_1, V_1$) zum Zustand ($p_2, V_2$) überzugehen. Umgekehrt repräsentiert die Fläche unter der Kurve der Absorbierte Wärme ($Q_C$), die von 2 bis 1 verläuft, die benötigte Energieentnahme, um vom Zustand ($p_2, V_2$) zurück zum Zustand ($p_1, V_1$) zu gelangen. Die Differenz zwischen diesen Flächen entspricht dem von beiden Kurven umschlossenen Bereich und repräsentiert der Effektive Arbeit ($W$), den das System ausführen kann.
Carnot zeigte auch, dass gemäß dem zweiten Hauptsatz der Thermodynamik der Wärme zugeführt ($Q_H$) nicht null sein kann. Dies impliziert, dass es keine Maschinen gibt, die in der Lage sind, die gesamte Wärme in Arbeit umzuwandeln.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexionen über die Triebkraft des Feuers und über Maschinen zur Entwicklung dieser Triebkraft), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, S. 393-457 (1872)
ID:(11131, 0)
Carnot-Zyklus zur Kühlung
Beschreibung
Wenn der Carnot-Prozess umgekehrt wird, kann er genutzt werden, um Wärme mithilfe von Arbeit zu übertragen, was als Wärmepumpe bezeichnet wird. In diesem Fall sieht das Diagramm folgendermaßen aus:
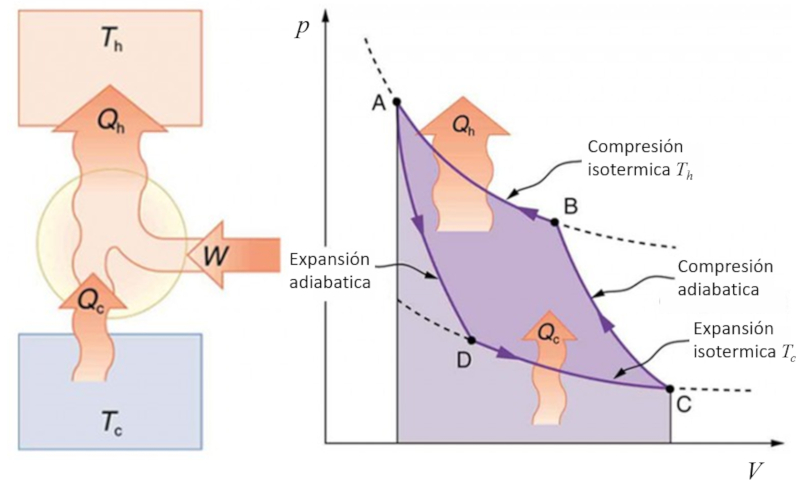
ID:(11143, 0)