Druyd:Knowledge

Der Otto-Zyklus

Storyboard

Der Otto-Zyklus entspricht einem Verbrennungsmotor, bei dem die Erwärmung mit konstantem Volumen erfolgt, indem das Gemisch nach dem Verdichten des Gases eingeschaltet wird.

>Modell

ID:(1486, 0)

Mechanismen

Konzept

Der Otto-Zyklus umfasst vier Hauptphasen: Ansaugen, Komprimieren, Arbeiten und Ausstoßen. Während der Ansaugphase zieht der Motor ein Gemisch aus Kraftstoff und Luft ein, während der Kolben nach unten bewegt wird. Das Gemisch wird dann komprimiert, wenn der Kolben nach oben bewegt wird, was die Temperatur und den Druck des Gases erhöht. Am oberen Punkt des Verdichtungshubs zündet die Zündkerze das komprimierte Gemisch, was zu einer schnellen Verbrennung führt, bekannt als Arbeitshub. Diese Verbrennung drückt den Kolben wieder nach unten und liefert so die Leistung für den Motor.

Nach dem Arbeitshub öffnet sich das Auslassventil und der Kolben bewegt sich wieder nach oben, um die verbrannten Gase aus dem Zylinder auszustoßen und damit den Zyklus zu vervollständigen. Der Motor wiederholt diesen Zyklus kontinuierlich während des Betriebs.

Die Effizienz eines Motors, der nach dem Otto-Zyklus arbeitet, hängt vom Verdichtungsgrad und den Eigenschaften des verwendeten Kraftstoffs ab. Höhere Verdichtungsverhältnisse führen in der Regel zu einer besseren Effizienz, erfordern jedoch einen Kraftstoff mit höherer Oktanzahl, um Motorklopfen zu verhindern. Der Otto-Zyklus zeichnet sich dadurch aus, dass er ein Hochgeschwindigkeitszyklus ist, bei dem jede Phase klar definiert ist, was wesentlich zur Gesamteffizienz und Leistungsabgabe der Motoren beiträgt, die ihn verwenden.

ID:(15282, 0)

Carnot-Zyklus

Konzept

Sadi Carnot führte [1] das theoretische Konzept der ersten Maschinenkonstruktion ein, die auf einem Temperaturgradienten basierend mechanische Arbeit erzeugen kann. Dies wird durch einen Prozess im Druck-Volumen-Raum erreicht, bei dem Wärme hinzugefügt und extrahiert wird, wie in der Abbildung dargestellt:

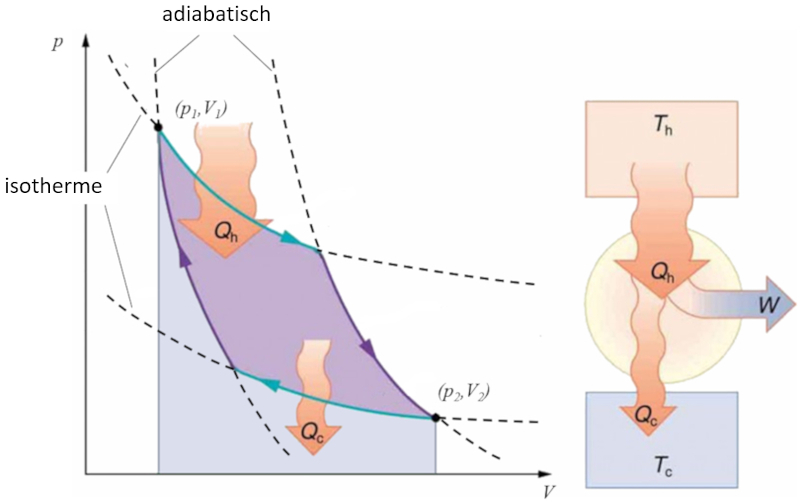
Die Fläche unter der Kurve der Wärme zugeführt ($Q_H$), die von 1 bis 2 reicht, repräsentiert die erforderliche Energiezufuhr, um vom Zustand ($p_1, V_1$) zum Zustand ($p_2, V_2$) überzugehen. Umgekehrt repräsentiert die Fläche unter der Kurve der Absorbierte Wärme ($Q_C$), die von 2 bis 1 verläuft, die benötigte Energieentnahme, um vom Zustand ($p_2, V_2$) zurück zum Zustand ($p_1, V_1$) zu gelangen. Die Differenz zwischen diesen Flächen entspricht dem von beiden Kurven umschlossenen Bereich und repräsentiert der Effektive Arbeit ($W$), den das System ausführen kann.

Carnot zeigte auch, dass gemäß dem zweiten Hauptsatz der Thermodynamik der Wärme zugeführt ($Q_H$) nicht null sein kann. Dies impliziert, dass es keine Maschinen gibt, die in der Lage sind, die gesamte Wärme in Arbeit umzuwandeln. [1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexionen über die Triebkraft des Feuers und über Maschinen zur Entwicklung dieser Triebkraft), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, S. 393-457 (1872)

ID:(11131, 0)

Otto-Zyklus: Druck-Volumen-Diagramm

Konzept

Der Otto-Zyklus [1] kann als eine technische Lösung basierend auf dem Carnot-Zyklus betrachtet werden. In diesem Zusammenhang besteht er aus vier Stufen, die wie folgt ablaufen:

• Stufe 1 bis 2: Adiabatische Kompression $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_2)$,
• Stufe 2 bis 3: Erwärmung $(p_2,V_2,T_2)\rightarrow(p_3,V_2,T_3)$,
• Stufe 3 bis 4: Adiabatische Expansion $(p_3,V_2,T_3)\rightarrow(p_4,V_1,T_4)$,
• Stufe 4 bis 1: Abkühlung $(p_4,V_1,T_4)\rightarrow(p_1,V_1,T_1)$

Diese Stufen werden im folgenden Diagramm dargestellt:

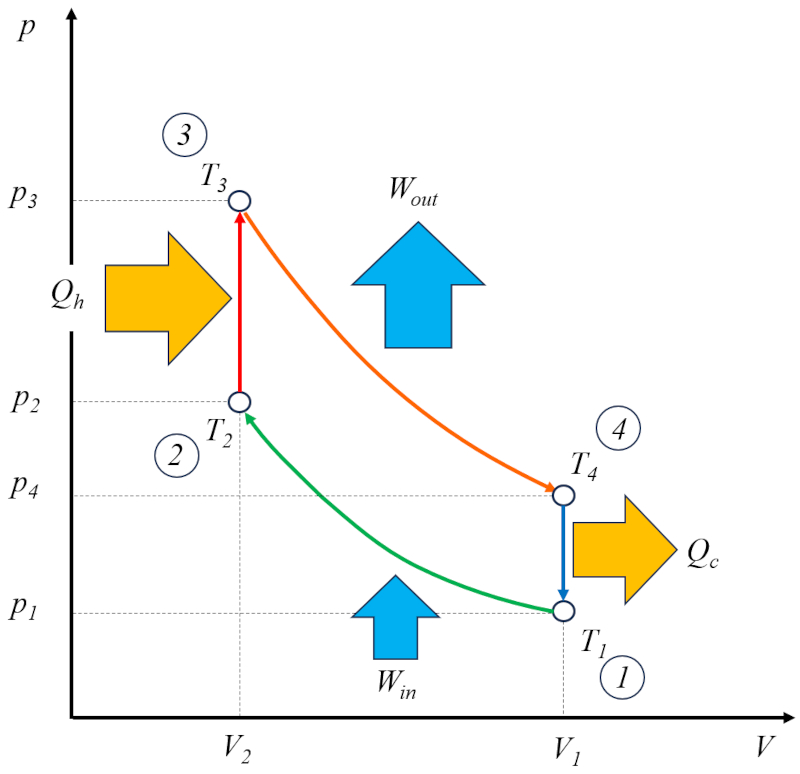
Auf dem Diagramm ist der Energiefluss dargestellt, bei dem der Wärme zugeführt ($Q_H$) Energie hinzufügt und die Temperatur von die Temperatur im Zustand 2 ($T_2$) auf die Temperatur im Zustand 3 ($T_3$) erhöht. Es tritt in das System ein und erbringt ein Effektive Arbeit ($W$) Einheiten Arbeit, während das Gegenstück der Absorbierte Wärme ($Q_C$) aufgenommen wird und die Temperatur von die Temperatur im Zustand 4 ($T_4$) auf die Temperatur im Zustand 1 ($T_1$) gesenkt wird. [1] "Verbrennungsmotor", N. A. Otto, Kaiserlichen Patentamts, Patent 532, 2. Januar 1877.Hinweis: Im Jahr 1862 versuchte Nikolaus Otto, den von Alphonse Beau de Rochas patentierten Verbrennungsmotor ohne Erfolg zu bauen. Später modifizierte er ihn und schaffte es 1877, einen funktionsfähigen Motor zu bauen, wobei er 30.000 leise und äußerst zuverlässige Motoren herstellte. Er patentierte sein Design im Jahr 1877; jedoch wurde das Patent später aufgrund des Bestehens des Patents von Alphonse Beau de Rochas widerrufen, obwohl Rochas nie seine Version bauen konnte. Da Otto der erste war, der den Motor zum Laufen brachte, erinnert seine Version heute an den Prozess als den "Otto-Zyklus".

ID:(11140, 0)

Technische Lösung

Konzept

Der Otto-Motor arbeitet in zwei Zyklen: dem eigentlichen Otto-Zyklus, der aus den folgenden Phasen besteht:

• Phase 1 bis 2: Adiabatische Kompression
• Phase 2 bis 3: Erwärmung
• Phase 3 bis 4: Adiabatische Expansion
• Phase 4 bis 1: Abkühlung

Zusätzlich gibt es einen Zyklus zum Entleeren der verbrannten Gase und zum Befüllen mit einer frischen Mischung.

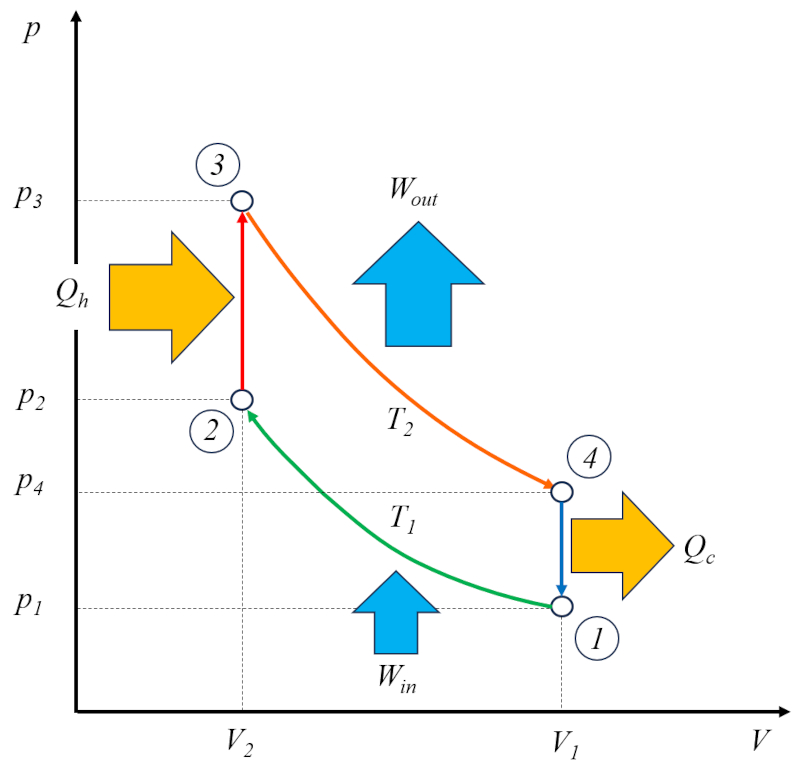
Aus diesem Grund wird er als Zweischichtmotor bezeichnet. Die Phase des Entleerens und Befüllens kann durch eine Ausgleichsmasse oder durch einen zweiten Zylinder durchgeführt werden, der außerhalb der Phase arbeitet.

Die Effizienz die Leistungsfähigkeit ($\eta$) des Motors kann mithilfe von der Otto-Kompressibilitätsfaktor ($r$) und der Adiabatischer Index ($\kappa$) mit folgender Gleichung geschätzt werden:

$ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$

ID:(11142, 0)

Wirkungsgrad in Abhängigkeit von den Temperaturen

Konzept

Der Absorbierte Wärme ($Q_C$) ist in Beziehung zu die Wärmekapazität bei konstantem Volumen ($C_V$), die Temperatur im Zustand 4 ($T_4$) und die Temperatur im Zustand 1 ($T_1$) gemäß der folgenden Gleichung:

$ Q_C = C_V ( T_4 - T_1 )$

Und der Wärme zugeführt ($Q_H$) ist in Beziehung zu die Wärmekapazität bei konstantem Volumen ($C_V$), die Temperatur im Zustand 3 ($T_3$) und die Temperatur im Zustand 2 ($T_2$) durch die folgende Gleichung:

$ Q_H = C_V ( T_3 - T_2 )$

Daher haben wir in der Gleichung für die Leistungsfähigkeit ($\eta$), dargestellt durch:

$ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $

Die folgende Beziehung:

$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

ID:(15749, 0)

Wirkungsgrad abhängig vom Kompressibilitätsfaktor

Konzept

Die Leistungsfähigkeit ($\eta$), in Bezug auf die Temperatur im Zustand 1 ($T_1$), die Temperatur im Zustand 2 ($T_2$), die Temperatur im Zustand 3 ($T_3$) und die Temperatur im Zustand 4 ($T_4$), wird mithilfe der folgenden Gleichung berechnet:

$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

Im Falle der adiabatischen Expansion wird sie durch der Adiabatischer Index ($\kappa$), der Erweitertes Volumen ($V_1$) und der Komprimiertes Volumen ($V_2$) beschrieben, gemäß der Beziehung:

$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$

Und die adiabatische Kompression wird durch die Beziehung repräsentiert:

$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$

Wenn wir die zweite Gleichung von der ersten subtrahieren, erhalten wir:

$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$

Dies führt zur Beziehung:

$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$

Dies wiederum führt zur Definition von der Otto-Kompressibilitätsfaktor ($r$) mit der folgenden Gleichung:

$ r =\displaystyle\frac{ V_1 }{ V_2 }$

Mit all diesen Komponenten kann die Effizienz eines Prozesses unter Verwendung des Otto-Zyklus wie folgt berechnet werden:

$ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$

ID:(15750, 0)

Modell

Konzept

ID:(15341, 0)

Der Otto-Zyklus

Beschreibung

Der Otto-Zyklus entspricht einem Verbrennungsmotor, bei dem die Erwärmung mit konstantem Volumen erfolgt, indem das Gemisch nach dem Verdichten des Gases eingeschaltet wird.

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$Q_C$

Q_C

Absorbierte Wärme

$\kappa$

kappa

Adiabatischer Index

$V_1$

V_1

Erweitertes Volumen

m^3

$V_2$

V_2

Komprimiertes Volumen

m^3

$\eta$

eta

Leistungsfähigkeit

$M$

Masse

$r$

Otto-Kompressibilitätsfaktor

$c_V$

c_V

Spezifische Wärme von Gasen bei konstantem Volumen

J/kg K

$T_1$

T_1

Temperatur im Zustand 1

$T_2$

T_2

Temperatur im Zustand 2

$T_3$

T_3

Temperatur im Zustand 3

$T_4$

T_4

Temperatur im Zustand 4

$Q_H$

Q_H

Wärme zugeführt

$C_V$

C_V

Wärmekapazität bei konstantem Volumen

J/kg

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

$ c_V =\displaystyle\frac{ C_V }{ M }$

c_V = C_V / M

Folgend einer Analogie zum ERROR:5219,0 f r Fl ssigkeiten und Feststoffe mit die Wärmekapazität ($C$) und die Masse ($M$):

$ c =\displaystyle\frac{ C }{ M }$

gibt es auch ein Spezifische Wärme von Gasen bei konstantem Volumen ($c_V$) f r das Erhitzen bei konstantem Volumen mit die Wärmekapazität bei konstantem Volumen ($C_V$):

$ c_V =\displaystyle\frac{ C_V }{ M }$

(ID 11113)

$ Q_C = C_V ( T_4 - T_1 )$

Q_C = C_V *( T_4 - T_1 )

Beim Entfernen von der Absorbierte Wärme ($Q_C$) steigt die Temperatur des Gases von $T_1$ auf $T_4$ in einem isobaren Prozess (bei konstantem Druck). Dies impliziert, dass wir die Beziehung f r ERROR:8085 mit die Wärmekapazität bei konstantem Volumen ($C_V$) und die Variación de Temperature ($\Delta T$) verwenden k nnen, die durch die Gleichung ausgedr ckt wird:

$ dU = C_V \Delta T $

Dies f hrt uns zu den Werten von die Temperatur im Zustand 1 ($T_1$) und die Temperatur im Zustand 4 ($T_4$) mittels der Formel:

$ Q_C = C_V ( T_4 - T_1 )$

(ID 11145)

$ Q_H = C_V ( T_3 - T_2 )$

Q_H = C_V *( T_3 - T_2 )

Durch die Zufuhr von der Wärme zugeführt ($Q_H$) steigt die Temperatur des Gases von $T_2$ auf $T_3$ in einem isochoren Prozess (bei konstantem Volumen). Dies bedeutet, dass wir die Beziehung f r ERROR:8085 mit die Wärmekapazität bei konstantem Volumen ($C_V$) und die Variación de Temperature ($\Delta T$) verwenden k nnen, die durch die folgende Gleichung ausgedr ckt wird:

$ dU = C_V \Delta T $

Dies f hrt zu den Werten von die Temperatur im Zustand 2 ($T_2$) und die Temperatur im Zustand 3 ($T_3$) wie folgt:

$ Q_H = C_V ( T_3 - T_2 )$

(ID 11157)

$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$

T_4 * V_1 ^( kappa -1)= T_3 V_2 ^( kappa - 1)

Bei einer adiabatischen Expansion erf llt das Gas die Beziehung, die der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$) einschlie t:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$

In diesem Fall vom Anfangspunkt 3 zum Punkt 4. Das bedeutet, dass w hrend der adiabatischen Expansion der Zustand des Gases von der Komprimiertes Volumen ($V_2$) und die Temperatur im Zustand 3 ($T_3$) zu der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 4 ($T_4$) wechselt, gem :

$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$

(ID 11159)

$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$

T_1 * V_1 ^( kappa -1)= T_2 V_2 ^( kappa - 1)

Angesichts dessen, dass bei einer adiabatischen Expansion das Gas die Beziehung zu der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$) erf llt:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$

In diesem Fall, vom anf nglichen Punkt 1 zum Punkt 2. Dies bedeutet, dass w hrend der adiabatischen Kompression der Zustand des Gases von der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 1 ($T_1$) zu der Komprimiertes Volumen ($V_2$) und die Temperatur im Zustand 2 ($T_2$) wie folgt ver ndert wird:

$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$

(ID 11160)

$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

eta =1-( T_4 - T_1 )/( T_3 - T_2 )

$ Q_C = C_V ( T_4 - T_1 )$

$ Q_H = C_V ( T_3 - T_2 )$

Daher haben wir in der Gleichung f r die Leistungsfähigkeit ($\eta$), dargestellt durch:

$ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $

Die folgende Beziehung:

$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

(ID 11161)

$ r =\displaystyle\frac{ V_1 }{ V_2 }$

r = V_1 / V_2

Die adiabatische Expansion wird mithilfe der Variablen der Adiabatischer Index ($\kappa$), die Temperatur im Zustand 4 ($T_4$), die Temperatur im Zustand 3 ($T_3$), der Erweitertes Volumen ($V_1$) und der Komprimiertes Volumen ($V_2$) durch die Beziehung

$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$

beschrieben, w hrend die adiabatische Kompression durch die Temperatur im Zustand 1 ($T_1$) und die Temperatur im Zustand 2 ($T_2$) mithilfe der Beziehung

$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$

dargestellt wird. Durch Subtrahieren der zweiten Gleichung von der ersten erhalten wir

$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$

Daraus ergibt sich die Beziehung

$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$

Und dies erm glicht es uns, der Otto-Kompressibilitätsfaktor ($r$) wie folgt zu definieren:

$ r =\displaystyle\frac{ V_1 }{ V_2 }$

(ID 11162)

$ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$

eta = 1 - 1/ r ^( kappa -1)

$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

Im Falle der adiabatischen Expansion wird sie durch der Adiabatischer Index ($\kappa$), der Erweitertes Volumen ($V_1$) und der Komprimiertes Volumen ($V_2$) beschrieben, gem der Beziehung:

$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$

Und die adiabatische Kompression wird durch die Beziehung repr sentiert:

$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$

Wenn wir die zweite Gleichung von der ersten subtrahieren, erhalten wir:

$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$

Dies f hrt zur Beziehung:

$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$

Dies wiederum f hrt zur Definition von der Otto-Kompressibilitätsfaktor ($r$) mit der folgenden Gleichung:

$ r =\displaystyle\frac{ V_1 }{ V_2 }$

Mit all diesen Komponenten kann die Effizienz eines Prozesses unter Verwendung des Otto-Zyklus wie folgt berechnet werden:

$ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$

(ID 11163)

Beispiele

Mechanismen

Der Otto-Zyklus umfasst vier Hauptphasen: Ansaugen, Komprimieren, Arbeiten und Aussto en. W hrend der Ansaugphase zieht der Motor ein Gemisch aus Kraftstoff und Luft ein, w hrend der Kolben nach unten bewegt wird. Das Gemisch wird dann komprimiert, wenn der Kolben nach oben bewegt wird, was die Temperatur und den Druck des Gases erh ht. Am oberen Punkt des Verdichtungshubs z ndet die Z ndkerze das komprimierte Gemisch, was zu einer schnellen Verbrennung f hrt, bekannt als Arbeitshub. Diese Verbrennung dr ckt den Kolben wieder nach unten und liefert so die Leistung f r den Motor.

Nach dem Arbeitshub ffnet sich das Auslassventil und der Kolben bewegt sich wieder nach oben, um die verbrannten Gase aus dem Zylinder auszusto en und damit den Zyklus zu vervollst ndigen. Der Motor wiederholt diesen Zyklus kontinuierlich w hrend des Betriebs.

Die Effizienz eines Motors, der nach dem Otto-Zyklus arbeitet, h ngt vom Verdichtungsgrad und den Eigenschaften des verwendeten Kraftstoffs ab. H here Verdichtungsverh ltnisse f hren in der Regel zu einer besseren Effizienz, erfordern jedoch einen Kraftstoff mit h herer Oktanzahl, um Motorklopfen zu verhindern. Der Otto-Zyklus zeichnet sich dadurch aus, dass er ein Hochgeschwindigkeitszyklus ist, bei dem jede Phase klar definiert ist, was wesentlich zur Gesamteffizienz und Leistungsabgabe der Motoren beitr gt, die ihn verwenden.

(ID 15282)

Carnot-Zyklus

Sadi Carnot f hrte [1] das theoretische Konzept der ersten Maschinenkonstruktion ein, die auf einem Temperaturgradienten basierend mechanische Arbeit erzeugen kann. Dies wird durch einen Prozess im Druck-Volumen-Raum erreicht, bei dem W rme hinzugef gt und extrahiert wird, wie in der Abbildung dargestellt:

Die Fl che unter der Kurve der Wärme zugeführt ($Q_H$), die von 1 bis 2 reicht, repr sentiert die erforderliche Energiezufuhr, um vom Zustand ($p_1, V_1$) zum Zustand ($p_2, V_2$) berzugehen. Umgekehrt repr sentiert die Fl che unter der Kurve der Absorbierte Wärme ($Q_C$), die von 2 bis 1 verl uft, die ben tigte Energieentnahme, um vom Zustand ($p_2, V_2$) zur ck zum Zustand ($p_1, V_1$) zu gelangen. Die Differenz zwischen diesen Fl chen entspricht dem von beiden Kurven umschlossenen Bereich und repr sentiert der Effektive Arbeit ($W$), den das System ausf hren kann.

Carnot zeigte auch, dass gem dem zweiten Hauptsatz der Thermodynamik der Wärme zugeführt ($Q_H$) nicht null sein kann. Dies impliziert, dass es keine Maschinen gibt, die in der Lage sind, die gesamte W rme in Arbeit umzuwandeln. [1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflexionen ber die Triebkraft des Feuers und ber Maschinen zur Entwicklung dieser Triebkraft), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, S. 393-457 (1872)

(ID 11131)

Otto-Zyklus: Druck-Volumen-Diagramm

Der Otto-Zyklus [1] kann als eine technische L sung basierend auf dem Carnot-Zyklus betrachtet werden. In diesem Zusammenhang besteht er aus vier Stufen, die wie folgt ablaufen:

• Stufe 1 bis 2: Adiabatische Kompression $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_2)$,
• Stufe 2 bis 3: Erw rmung $(p_2,V_2,T_2)\rightarrow(p_3,V_2,T_3)$,
• Stufe 3 bis 4: Adiabatische Expansion $(p_3,V_2,T_3)\rightarrow(p_4,V_1,T_4)$,
• Stufe 4 bis 1: Abk hlung $(p_4,V_1,T_4)\rightarrow(p_1,V_1,T_1)$

Diese Stufen werden im folgenden Diagramm dargestellt:

Auf dem Diagramm ist der Energiefluss dargestellt, bei dem der Wärme zugeführt ($Q_H$) Energie hinzuf gt und die Temperatur von die Temperatur im Zustand 2 ($T_2$) auf die Temperatur im Zustand 3 ($T_3$) erh ht. Es tritt in das System ein und erbringt ein Effektive Arbeit ($W$) Einheiten Arbeit, w hrend das Gegenst ck der Absorbierte Wärme ($Q_C$) aufgenommen wird und die Temperatur von die Temperatur im Zustand 4 ($T_4$) auf die Temperatur im Zustand 1 ($T_1$) gesenkt wird. [1] "Verbrennungsmotor", N. A. Otto, Kaiserlichen Patentamts, Patent 532, 2. Januar 1877.Hinweis: Im Jahr 1862 versuchte Nikolaus Otto, den von Alphonse Beau de Rochas patentierten Verbrennungsmotor ohne Erfolg zu bauen. Sp ter modifizierte er ihn und schaffte es 1877, einen funktionsf higen Motor zu bauen, wobei er 30.000 leise und u erst zuverl ssige Motoren herstellte. Er patentierte sein Design im Jahr 1877; jedoch wurde das Patent sp ter aufgrund des Bestehens des Patents von Alphonse Beau de Rochas widerrufen, obwohl Rochas nie seine Version bauen konnte. Da Otto der erste war, der den Motor zum Laufen brachte, erinnert seine Version heute an den Prozess als den "Otto-Zyklus".

(ID 11140)

Technische L sung

Der Otto-Motor arbeitet in zwei Zyklen: dem eigentlichen Otto-Zyklus, der aus den folgenden Phasen besteht:

• Phase 1 bis 2: Adiabatische Kompression
• Phase 2 bis 3: Erw rmung
• Phase 3 bis 4: Adiabatische Expansion
• Phase 4 bis 1: Abk hlung

Zus tzlich gibt es einen Zyklus zum Entleeren der verbrannten Gase und zum Bef llen mit einer frischen Mischung.

Aus diesem Grund wird er als Zweischichtmotor bezeichnet. Die Phase des Entleerens und Bef llens kann durch eine Ausgleichsmasse oder durch einen zweiten Zylinder durchgef hrt werden, der au erhalb der Phase arbeitet.

Die Effizienz die Leistungsfähigkeit ($\eta$) des Motors kann mithilfe von der Otto-Kompressibilitätsfaktor ($r$) und der Adiabatischer Index ($\kappa$) mit folgender Gleichung gesch tzt werden:

$ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$

(ID 11142)

Wirkungsgrad in Abh ngigkeit von den Temperaturen

$ Q_C = C_V ( T_4 - T_1 )$

$ Q_H = C_V ( T_3 - T_2 )$

Daher haben wir in der Gleichung f r die Leistungsfähigkeit ($\eta$), dargestellt durch:

$ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $

Die folgende Beziehung:

$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

(ID 15749)

Wirkungsgrad abh ngig vom Kompressibilit tsfaktor

$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

Im Falle der adiabatischen Expansion wird sie durch der Adiabatischer Index ($\kappa$), der Erweitertes Volumen ($V_1$) und der Komprimiertes Volumen ($V_2$) beschrieben, gem der Beziehung:

$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$

Und die adiabatische Kompression wird durch die Beziehung repr sentiert:

$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$

Wenn wir die zweite Gleichung von der ersten subtrahieren, erhalten wir:

$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$

Dies f hrt zur Beziehung:

$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$

Dies wiederum f hrt zur Definition von der Otto-Kompressibilitätsfaktor ($r$) mit der folgenden Gleichung:

$ r =\displaystyle\frac{ V_1 }{ V_2 }$

Mit all diesen Komponenten kann die Effizienz eines Prozesses unter Verwendung des Otto-Zyklus wie folgt berechnet werden:

$ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$

(ID 15750)

Modell

(ID 15341)

ID:(1486, 0)