Benützer:
Der Carnot-Zyklus
Storyboard 
Der Carnot-Zyklus ist ein allgemeiner Zyklus im Druck-Volumen-Raum, der zeigt, wie im Prinzip eine thermodynamische Maschine gebaut werden kann, die den Wärmefluss in mechanische Arbeit umwandelt.
ID:(1488, 0)
Mechanismen
Iframe
Der Zyklus besteht aus vier reversiblen Prozessen: zwei isothermen (konstante Temperatur) und zwei adiabatischen (kein Wärmeaustausch). Während der isothermen Expansion absorbiert das System (typischerweise ein Gas) Wärme aus einem Hochtemperaturreservoir, expandiert und verrichtet Arbeit an der Umgebung. Dies wird gefolgt von einer adiabatischen Expansion, bei der das System weiterhin Arbeit verrichtet, aber ohne Wärmeaustausch, was zu einer Abkühlung führt. Anschließend durchläuft das Gas eine isotherme Kompression, gibt Wärme an ein kühleres Reservoir ab, während am Gas gearbeitet wird, um es zu komprimieren. Der Zyklus endet mit einer adiabatischen Kompression, die die Temperatur des Gases weiter erhöht und es in seinen ursprünglichen Zustand zurückführt.
Die Schönheit des Carnot-Zyklus liegt in seiner Einfachheit und der Einsicht, die er in die Effizienzgrenzen aller wärmebasierten Motoren bietet. Die Effizienz eines Carnot-Motors hängt nur von den Temperaturen der heißen und kalten Reservoirs ab und ist unabhängig von der Arbeitssubstanz oder den Details des Prozesses selbst. Diese Effizienz wird als das Verhältnis der Temperaturdifferenz zwischen den Reservoirs zur höheren Temperatur ausgedrückt, was zeigt, dass kein realer Motor, der zwischen zwei Wärmereservoirs arbeitet, effizienter sein kann als ein Carnot-Motor, der zwischen denselben Reservoirs arbeitet.
Mechanismen
ID:(15281, 0)
Carnot-Zyklus: Schema einer Maschine
Konzept
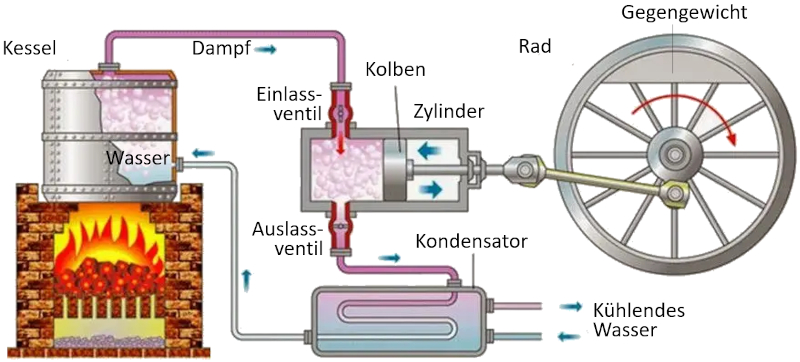
In einer Maschine, die das Konzept von Carnot verwendet, finden folgende Prozesse statt:
• Der Reservoir mit der höheren Temperatur wird mit einem Ofen erzeugt.
• Der Reservoir mit der niedrigeren Temperatur wird durch ein Kühlsystem erzeugt.
• Der aus dem Reservoir erzeugte Dampf expandiert zu einem Gas, wodurch der Kolben verdrängt wird und die Ausgleichsmasse angehoben wird. In der ersten isothermen Phase ist das erste Ventil geöffnet, während das zweite Ventil geschlossen ist. In der zweiten Phase des Prozesses wird das erste Ventil geschlossen, und die Expansion erfolgt adiabatisch.
• In der dritten Phase wird das zweite Ventil geöffnet und mit Hilfe der Ausgleichsmasse wird der Kolben zurückgeführt und das Gas isotherm ausgestoßen. In der vierten Phase wird das Ventil geschlossen, und der Prozess endet adiabatisch.
ID:(11134, 0)
Carnot-Zyklus
Konzept
Sadi Carnot führte [1] das theoretische Konzept der ersten Maschinenkonstruktion ein, die auf einem Temperaturgradienten basierend mechanische Arbeit erzeugen kann. Dies wird durch einen Prozess im Druck-Volumen-Raum erreicht, bei dem Wärme hinzugefügt und extrahiert wird, wie in der Abbildung dargestellt:
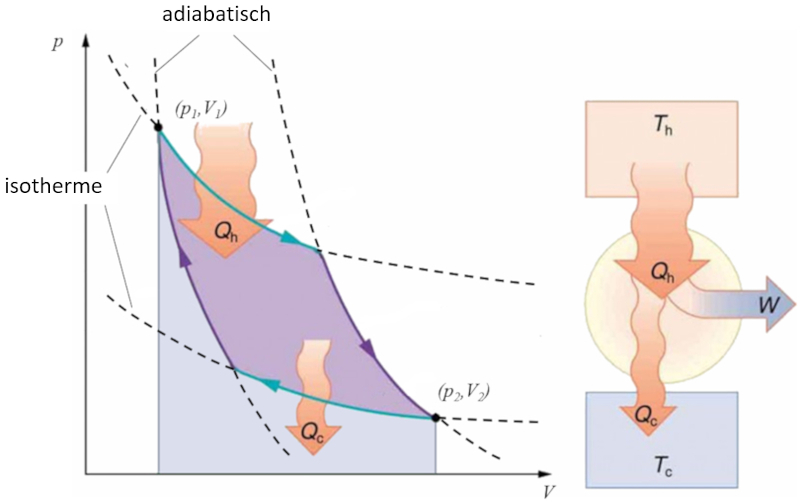
Die Fläche unter der Kurve der Wärme zugeführt ($Q_H$), die von 1 bis 2 reicht, repräsentiert die erforderliche Energiezufuhr, um vom Zustand ($p_1, V_1$) zum Zustand ($p_2, V_2$) überzugehen. Umgekehrt repräsentiert die Fläche unter der Kurve der Absorbierte Wärme ($Q_C$), die von 2 bis 1 verläuft, die benötigte Energieentnahme, um vom Zustand ($p_2, V_2$) zurück zum Zustand ($p_1, V_1$) zu gelangen. Die Differenz zwischen diesen Flächen entspricht dem von beiden Kurven umschlossenen Bereich und repräsentiert der Effektive Arbeit ($W$), den das System ausführen kann.
Carnot zeigte auch, dass gemäß dem zweiten Hauptsatz der Thermodynamik der Wärme zugeführt ($Q_H$) nicht null sein kann. Dies impliziert, dass es keine Maschinen gibt, die in der Lage sind, die gesamte Wärme in Arbeit umzuwandeln.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexionen über die Triebkraft des Feuers und über Maschinen zur Entwicklung dieser Triebkraft), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, S. 393-457 (1872)
ID:(11131, 0)
Anwendung im einfachen Druck-Volumen-Diagramm
Konzept
Der Carnot-Prozess wird einfach als ein Zyklus beschrieben, bei dem abwechselnd isotherm und adiabatisch gearbeitet wird. Insbesondere werden Druck-Volumen- und Temperatur-Entropie-Diagramme untersucht. Im ersten Fall können die vier Stufen wie folgt identifiziert werden:
Stufe 1 zu 2: Isotherme Expansion.
Stufe 2 zu 3: Adiabatische Expansion.
Stufe 3 zu 4: Isotherme Kompression.
Stufe 4 zu 1: Adiabatische Kompression.
Diese Stufen sind unten dargestellt:
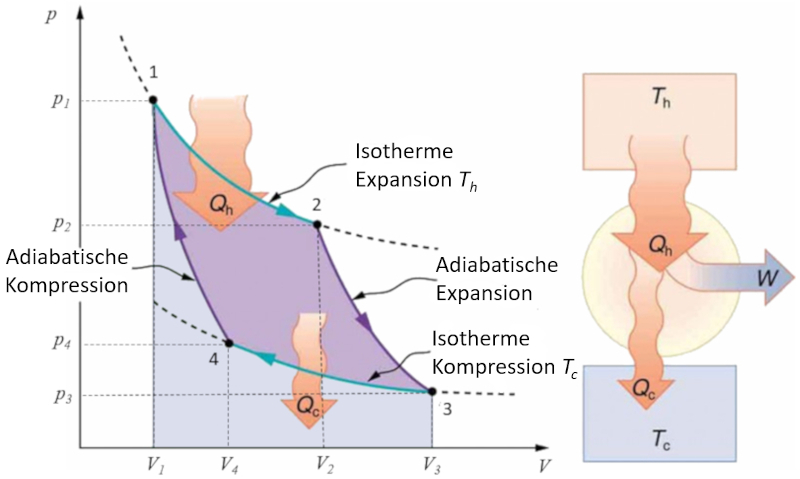
Das beigefügte Diagramm veranschaulicht den Energiefluss, wobei der Wärme zugeführt ($Q_H$) (heiß) das Reservoir bei die Hohe Temperatur ($T_H$) verlässt, in das System eintritt, Arbeit $W$ verrichtet, während das komplementäre Absorbierte Wärme ($Q_C$) (kalt) vom Reservoir bei die Niedrige Temperatur ($T_C$) aufgenommen wird.
ID:(11132, 0)
Anwendung im einfachen Temperatur-Entropie-Diagramm
Konzept
Der Carnot-Zyklus wird einfach als ein Zyklus beschrieben, bei dem abwechselnd isotherm und adiabatisch gearbeitet wird. Insbesondere werden die Druck-Volumen- und Temperatur-Entropie-Diagramme untersucht. Im Fall des Temperatur-Entropie-Diagramms wird das Diagramm vereinfacht, indem von isothermen Stadien zu konstanten Entropie-Stadien übergegangen wird:
Im Temperatur-Entropie-Diagramm werden die konstanten Entropie-Stadien wie folgt dargestellt:
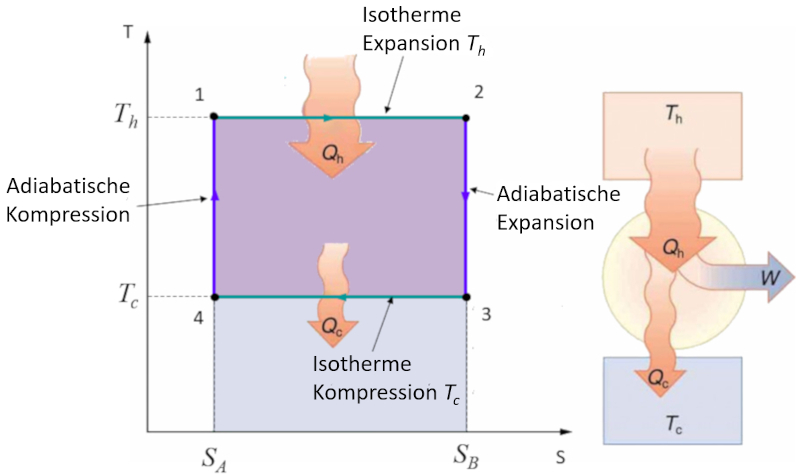
Während dieser Phasen bleibt die Entropie ($S$) konstant, was bedeutet, dass keine Wärmeübertragung stattfindet, während die Absolute Temperatur ($T$) variieren kann. Dies vereinfacht die Darstellung des Zyklus und ermöglicht eine direktere Analyse der thermodynamischen Eigenschaften des Systems.
ID:(11133, 0)
Ausgeführte Arbeit
Konzept
Da der Differential ungenaue Arbeits ($\delta W$) in Abhängigkeit von die Druck ($p$) und die Volumenvariation ($dV$) wie folgt definiert ist:
| $ \delta W = p dV $ |
Können wir der Effektive Arbeit ($W$) berechnen, indem wir entlang der Kurven des Zyklusdiagramms integrieren:
$W = \displaystyle\oint pdV$
Mit Hilfe des ersten Hauptsatzes der Thermodynamik mit der Interne Energiedifferenz ($dU$) und der Differential ungenau Wärme ($\delta Q$) ergibt sich:
| $ dU = \delta Q - \delta W $ |
Und unter Berücksichtigung des Pfads im Diagramm von die Absolute Temperatur ($T$) und die Entropie ($S$) erhalten wir mit die Entropievariation ($dS$):
$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$
Da das Integral entlang eines geschlossenen Pfads eines exakten Differentials gleich null ist, ergibt sich:
| $ W = \displaystyle\oint T dS$ |
ID:(10264, 0)
Leistung basierend auf Wärmeströme
Konzept
Da die Leistungsfähigkeit ($\eta$) mit der Effektive Arbeit ($W$) und der Wärme zugeführt ($Q_H$) ist
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
kann es mit der Effektive Arbeit ($W$), das zusammen mit der Wärme zugeführt ($Q_H$) und der Absorbierte Wärme ($Q_C$) steht, ersetzt werden und ergibt
| $ W = Q_H - Q_C $ |
und liefert die folgende Beziehung:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
ID:(10262, 0)
Leistung abhängig von den Temperaturen
Konzept
Die Leistungsfähigkeit ($\eta$) ist eine Funktion von der Wärme zugeführt ($Q_H$) und der Absorbierte Wärme ($Q_C$), gegeben durch:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Wir können der Wärme zugeführt ($Q_H$) in Bezug auf die Niedrige Temperatur ($T_C$), die Niedrige Entropie ($S_C$) und die Hohe Entropie ($S_H$) ausdrücken als:
| $ Q_C = T_C ( S_H - S_C ) $ |
Und unter Verwendung von die Hohe Temperatur ($T_H$) als:
| $ Q_H = T_H ( S_H - S_C ) $ |
Wenn wir diese Ausdrücke ersetzen, erhalten wir:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
ID:(10260, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $
eta = 1 - Q_C / Q_H
$ \eta \equiv \displaystyle\frac{ W }{ Q_H } $
eta = W / Q_H
$ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $
eta =1 - T_C / T_H
$ Q_C = T_C ( S_H - S_C ) $
Q_C = T_C *( S_H - S_C )
$ Q_H = T_H ( S_H - S_C ) $
Q_H = T_H *( S_H - S_C )
$ W = Q_H - Q_C $
W = Q_H - Q_C
ID:(15340, 0)
Arbeit generiert
Gleichung
Wenn im Carnot-Zyklus der Wärme zugeführt ($Q_H$) aus dem Reservoir mit höherer Temperatur entnommen und der Absorbierte Wärme ($Q_C$) dem Reservoir mit niedrigerer Temperatur zugeführt wird, wird ein Effektive Arbeit ($W$) erzeugt, was gleich ist:
| $ W = Q_H - Q_C $ |
ID:(11135, 0)
Wärmeaufnahme
Gleichung
Der Absorbierte Wärme ($Q_C$) aufgrund der Differenz in der Entropie gleich die Niedrige Temperatur ($T_C$) ist, nämlich die Hohe Entropie ($S_H$) und die Niedrige Entropie ($S_C$):
| $ Q_C = T_C ( S_H - S_C ) $ |
Da der Effektive Arbeit ($W$) gleich dem Integral entlang eines geschlossenen Pfads im Raum die Absolute Temperatur ($T$) und die Entropie ($S$) ist, haben wir:
| $ W = \displaystyle\oint T dS$ |
Bei Betrachtung des Temperatur-Entropie-Diagramms sehen wir, dass die aufgenommene Wärme der Absorbierte Wärme ($Q_C$) aufgrund der Differenz in der Entropie gleich die Niedrige Temperatur ($T_C$) ist, nämlich die Hohe Entropie ($S_H$) und die Niedrige Entropie ($S_C$):
| $ Q_C = T_C ( S_H - S_C ) $ |
ID:(11138, 0)
Abgeführt Wärme
Gleichung
Der Wärme zugeführt ($Q_H$) aufgrund der Differenz in der Entropie gleich die Hohe Temperatur ($T_H$) ist, nämlich die Hohe Entropie ($S_H$) und die Niedrige Entropie ($S_C$):
| $ Q_H = T_H ( S_H - S_C ) $ |
Da der Effektive Arbeit ($W$) gleich dem Integral entlang eines geschlossenen Pfads im Raum die Absolute Temperatur ($T$) und die Entropie ($S$) ist, haben wir:
| $ W = \displaystyle\oint T dS$ |
Beim Konsultieren des Temperatur-Entropie-Diagramms sehen wir, dass die aufgenommene Wärme der Wärme zugeführt ($Q_H$) aufgrund der Differenz in der Entropie gleich die Hohe Temperatur ($T_H$) ist, nämlich die Hohe Entropie ($S_H$) und die Niedrige Entropie ($S_C$):
| $ Q_H = T_H ( S_H - S_C ) $ |
ID:(11137, 0)
Leistung
Gleichung
Die Leistungsfähigkeit ($\eta$) kann definiert werden als der Prozentsatz, den der Effektive Arbeit ($W$) in Bezug auf der Wärme zugeführt ($Q_H$):
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
.
ID:(11154, 0)
Leistung basierend auf Wärmeströme
Gleichung
Die Leistungsfähigkeit ($\eta$) kann aus der Wärme zugeführt ($Q_H$) und der Absorbierte Wärme ($Q_C$) berechnet werden
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Da die Leistungsfähigkeit ($\eta$) mit der Effektive Arbeit ($W$) und der Wärme zugeführt ($Q_H$) ist
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
kann es mit der Effektive Arbeit ($W$), das zusammen mit der Wärme zugeführt ($Q_H$) und der Absorbierte Wärme ($Q_C$) steht, ersetzt werden und ergibt
| $ W = Q_H - Q_C $ |
und liefert die folgende Beziehung:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
ID:(11155, 0)
Leistung abhängig von den Temperaturen
Gleichung
Die Leistungsfähigkeit ($\eta$) kann basierend auf Hohe Temperatur ($T_H$) und Niedrige Temperatur ($T_C$) berechnet werden mit:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
Die Leistungsfähigkeit ($\eta$) ist eine Funktion von der Wärme zugeführt ($Q_H$) und der Absorbierte Wärme ($Q_C$), gegeben durch:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Wir können der Wärme zugeführt ($Q_H$) in Bezug auf die Niedrige Temperatur ($T_C$), die Niedrige Entropie ($S_C$) und die Hohe Entropie ($S_H$) ausdrücken als:
| $ Q_C = T_C ( S_H - S_C ) $ |
Und unter Verwendung von die Hohe Temperatur ($T_H$) als:
| $ Q_H = T_H ( S_H - S_C ) $ |
Wenn wir diese Ausdrücke ersetzen, erhalten wir:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
ID:(11136, 0)