Utilisateur:
Représentation graphique des travaux à investir
Noter 
Pour répéter le processus, il est nécessaire de revenir du volume $V_2$ au volume $V_1$, ce qui signifie suivre une courbe dans le diagramme pression-volume dans le sens inverse :
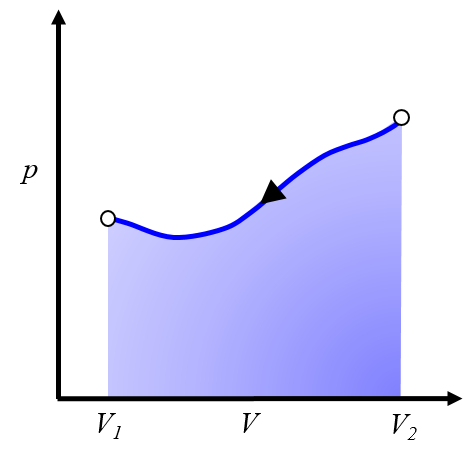
Cela représente un travail à investir, que nous devons fournir pour répéter le cycle.
Généralement, ce processus est réalisé en refroidissant le système, ce qui le fait se contracter. L'énergie à investir correspond à la chaleur retirée du système.
ID:(10254, 0)
Représentation graphique du travail effectif obtenu
Citation
Le travail net obtenu est la différence entre le travail obtenu et le travail nécessaire pour compléter le cycle :
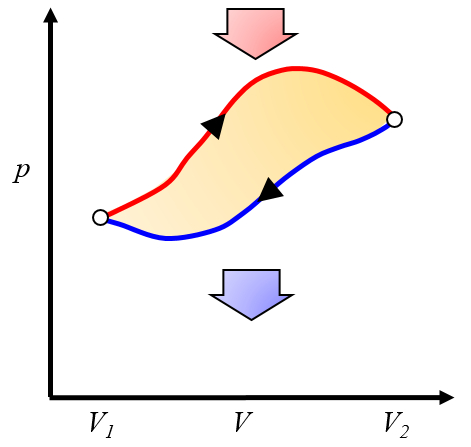
ID:(10268, 0)
Représentation graphique du travail obtenu
Exercer
Étant donné que le travail est
| $ \delta W = p dV $ |
il peut être représenté sur un graphique pression-volume comme la zone sous la courbe de pression en fonction du volume :
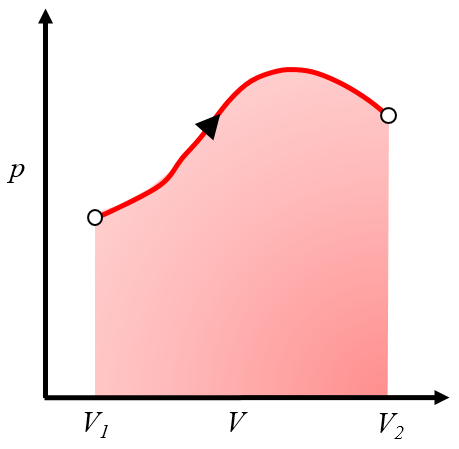
Cette zone représente le travail obtenu lorsque un gaz effectue un travail en s'expansant du volume $V_1$ au volume $V_2$.
Généralement, ce processus est réalisé en chauffant le système, ce qui le fait s'étendre et effectuer le travail. Un exemple serait un piston avec du gaz chauffé dans une chaudière.
ID:(10266, 0)
Cycle de Carnot : schéma d'une machine
Équation
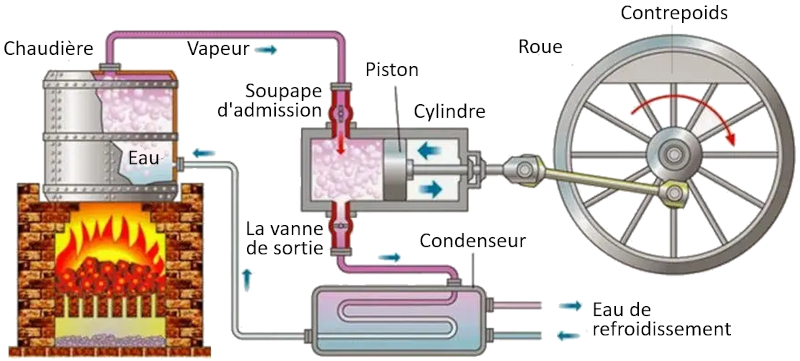
Dans une machine qui utilise le concept de Carnot, les processus suivants ont lieu :
• Le réservoir à température la plus élevée est créé à l'aide d'un four.
• Le réservoir à température la plus basse est créé à l'aide d'un système de réfrigération.
• La vapeur générée à partir du réservoir se dilate en un gaz, déplaçant le piston et soulevant la masse de compensation. Dans la première étape isotherme, la première vanne est ouverte tandis que la deuxième est fermée. Dans la deuxième étape du processus, la première vanne est fermée et l'expansion se poursuit de manière adiabatique.
• Dans la troisième étape, la deuxième vanne est ouverte et, avec l'aide de la masse de compensation, le piston est ramené et le gaz est expulsé de manière isotherme. Dans la quatrième étape, la vanne est fermée et le processus se termine de manière adiabatique.
ID:(11134, 0)
Cycle de Carnot
Script
Sadi Carnot a introduit [1] le concept théorique du premier projet de machine capable de générer du travail mécanique basé sur un gradient de température. Cela est réalisé grâce à un processus dans l'espace pression-volume où la chaleur est ajoutée et extraite, comme illustré dans l'image :
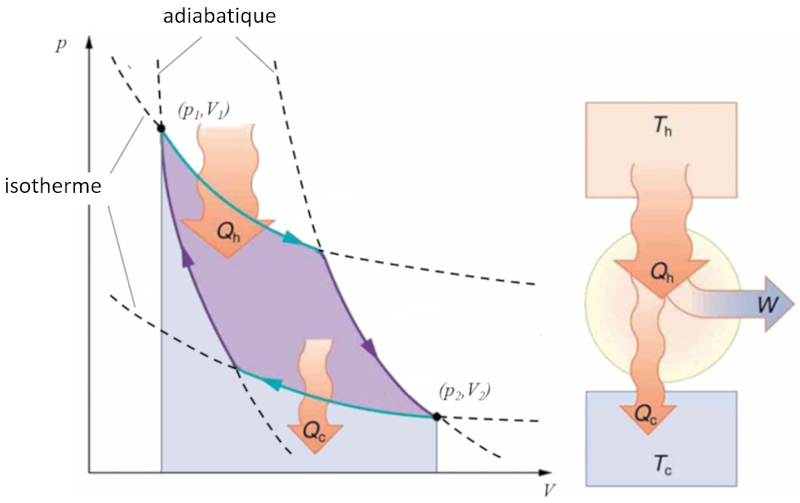
La zone sous la courbe le chaleur fournie ($Q_H$), s'étendant de 1 à 2, représente l'énergie nécessaire pour passer de l'état ($p_1, V_1$) à l'état ($p_2, V_2$). En revanche, la zone sous la courbe le chaleur absorbée ($Q_C$), allant de 2 à 1, représente l'extraction d'énergie nécessaire pour revenir de l'état ($p_2, V_2$) à l'état ($p_1, V_1$). La différence entre ces zones correspond à la région délimitée par les deux courbes et représente le travail efficace ($W$) que le système peut accomplir.
Carnot a également démontré que, conformément au deuxième principe de la thermodynamique, le chaleur fournie ($Q_H$) ne peut pas être nul. Cela implique qu'il n'existe pas de machines capables de convertir toute la chaleur en travail.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance", Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Cycle de Carnot pour la réfrigération
Variable
Si le processus de Carnot est inversé, on peut utiliser du travail pour transférer de la chaleur, ce qui est appelé une pompe à chaleur. Dans ce cas, le diagramme est le suivant :
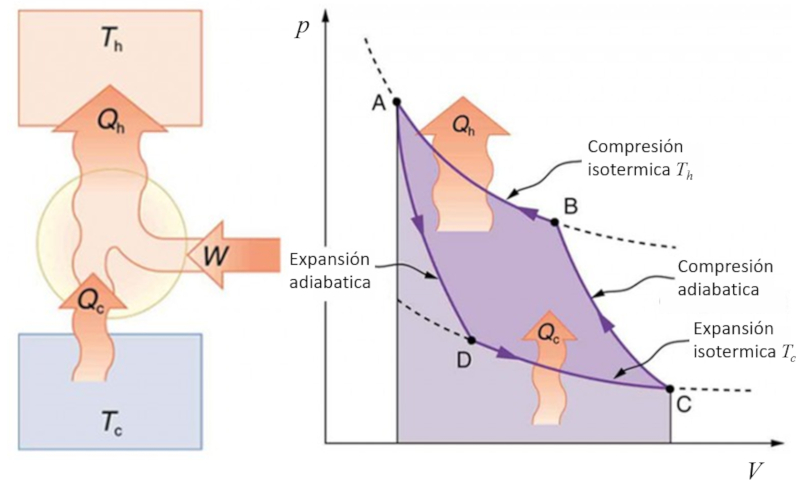
ID:(11143, 0)