Benützer:


Der Diesel-Zyklus
Storyboard

Der Dieseltakt entspricht einem Verbrennungsmotor, bei dem die Erwärmung bei konstantem Druck erfolgt und sich das Gas bei der Zündung des Gemisches ausdehnt.

>Modell

ID:(1487, 0)


Mechanismen
Konzept

Der Dieselzyklus ist ein thermodynamischer Kreislauf, der die Grundlage für Dieselmotoren bildet, die häufig in Fahrzeugen und Industriemaschinen verwendet werden. Entwickelt von Rudolf Diesel in den 1890er Jahren, unterscheidet sich dieser Zyklus hauptsächlich in seinem Zündprozess vom Otto-Zyklus der Benzinmotoren. Im Dieselzyklus wird Luft in den Zylinder gezogen und zu einem viel höheren Verhältnis als bei Benzinmotoren komprimiert, was ihre Temperatur so weit erhöht, dass Dieselkraftstoff ohne Zündkerze entzündet werden kann.

Während des Betriebs beginnt der Zyklus mit dem Einziehen von Luft durch den nach unten bewegenden Kolben. Die Luft wird dann beim Aufwärtshub komprimiert, wodurch ihre Temperatur steigt. Auf dem Höhepunkt der Kompressionsphase wird Kraftstoff als feiner Nebel in die heiße komprimierte Luft eingespritzt, was zu einer spontanen Zündung führt. Die Verbrennung treibt den Kolben nach unten und erzeugt so Energie. Schließlich werden die Verbrennungsgase in der Ausstoßphase ausgestoßen, wenn der Kolben wieder nach oben bewegt wird und den Zyklus abschließt.

Dieselmotoren sind für ihre Effizienz und Langlebigkeit bekannt. Das hohe Kompressionsverhältnis ermöglicht es nicht nur, mehr Energie aus dem Kraftstoff zu extrahieren, sondern erhöht auch die thermische Effizienz, was bedeutet, dass ein größerer Anteil der Energie des Kraftstoffs in mechanische Arbeit umgewandelt wird. Dieselmotoren bieten in der Regel eine bessere Kraftstoffeffizienz und produzieren weniger CO2-Emissionen pro Energieeinheit als ihre Benzin-Gegenstücke, können jedoch höhere Emissionen anderer Schadstoffe wie Stickoxide und Partikel emittieren.

ID:(15283, 0)


Carnot-Zyklus
Konzept

Sadi Carnot führte [1] das theoretische Konzept der ersten Maschinenkonstruktion ein, die auf einem Temperaturgradienten basierend mechanische Arbeit erzeugen kann. Dies wird durch einen Prozess im Druck-Volumen-Raum erreicht, bei dem Wärme hinzugefügt und extrahiert wird, wie in der Abbildung dargestellt:



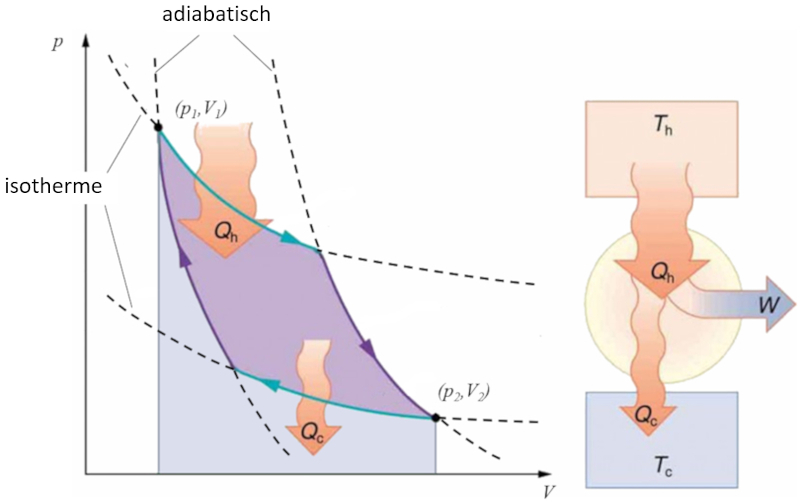
Die Fläche unter der Kurve der Wärme zugeführt ($Q_H$), die von 1 bis 2 reicht, repräsentiert die erforderliche Energiezufuhr, um vom Zustand ($p_1, V_1$) zum Zustand ($p_2, V_2$) überzugehen. Umgekehrt repräsentiert die Fläche unter der Kurve der Absorbierte Wärme ($Q_C$), die von 2 bis 1 verläuft, die benötigte Energieentnahme, um vom Zustand ($p_2, V_2$) zurück zum Zustand ($p_1, V_1$) zu gelangen. Die Differenz zwischen diesen Flächen entspricht dem von beiden Kurven umschlossenen Bereich und repräsentiert der Effektive Arbeit ($W$), den das System ausführen kann.

Carnot zeigte auch, dass gemäß dem zweiten Hauptsatz der Thermodynamik der Wärme zugeführt ($Q_H$) nicht null sein kann. Dies impliziert, dass es keine Maschinen gibt, die in der Lage sind, die gesamte Wärme in Arbeit umzuwandeln. [1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexionen über die Triebkraft des Feuers und über Maschinen zur Entwicklung dieser Triebkraft), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, S. 393-457 (1872)

ID:(11131, 0)


Dieselkreislauf: Druck-Volumen-Diagramm
Konzept

Rudolf Diesel [1] hatte das Ziel, einen Zyklus zu entwickeln, der sich vom Carnot-Zyklus unterscheidet und eine höhere Effizienz im Vergleich zum Otto-Zyklus erreicht. Dieser Prozess verläuft in den folgenden Stufen:

• Stufe 1 bis 2: Adiabatische Verdichtung $(p_1,V_1,T_1)\rightarrow (p_2,V_2,T_2)$,
• Stufe 2 bis 3: Erwärmung und Expansion bei konstantem Druck $(p_2,V_2,T_2)\rightarrow (p_2,V_3,T_3)$,
• Stufe 3 bis 4: Adiabatische Expansion $(p_2,V_3,T_3)\rightarrow (p_3,V_1,T_4)$,
• Stufe 4 bis 1: Abkühlung bei konstantem Volumen $(p_3,V_1,T_4)\rightarrow (p_1,V_1,T_1)$

Diese Stufen sind nachfolgend dargestellt:

Der Schlüssel liegt in Stufe 2 bis 3, wo die Expansion bei konstantem Druck erfolgt. Der Grund wird deutlich, wenn man sich das Diagramm ansieht:

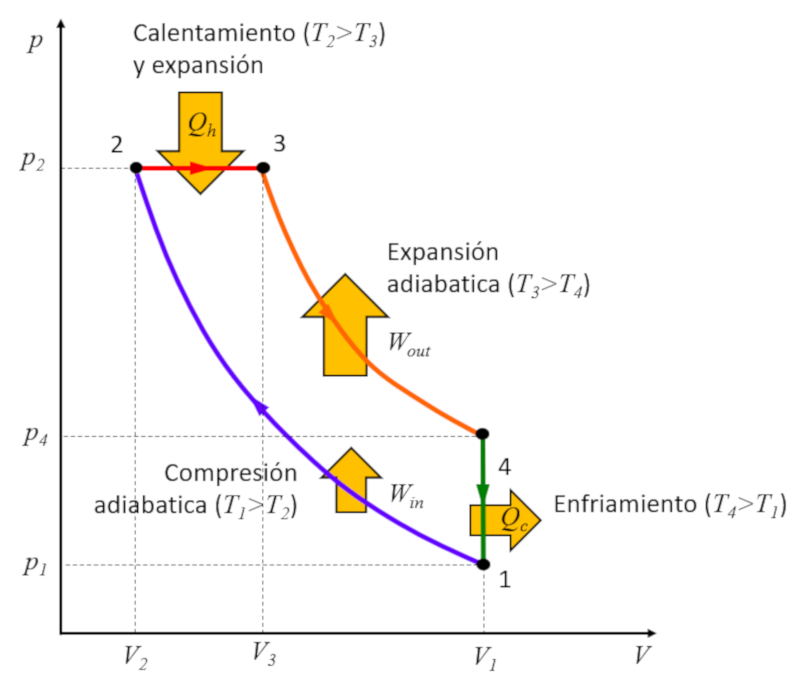
Die gewonnene Energie entspricht der Fläche innerhalb des Zyklus, und durch die Kompression bei konstantem Druck ist diese Fläche größer als im Fall der Kompression bei konstantem Volumen. [1] "Verfahren zur Entwickelung eines rationellen Wärmemotors zum Ersatz der Dampfmaschine und der heute bekannten Verbrennungsmotoren" (Verfahren zur Entwicklung eines rationalen Wärmemotors zur Ersetzung der Dampfmaschine und der heutigen bekannten Verbrennungsmotoren), Rudolf Diesel, Kaiserlichen Patentamts, Nr. 67207 (1892)

ID:(11141, 0)


Effizienzanalyse
Konzept

Sowohl der Otto-Zyklus als auch der Dieselmotor-Zyklus sind abhängig von den Variablen die Temperatur im Zustand 1 ($T_1$), die Temperatur im Zustand 2 ($T_2$), die Temperatur im Zustand 3 ($T_3$) und die Temperatur im Zustand 4 ($T_4$). Im Falle des Dieselmotor-Zyklus hängt er auch von der Adiabatischer Index ($\kappa$) ab, dessen Wert 1,4 beträgt.

Im Otto-Zyklus wird die Effizienz basierend auf der Temperatur mit der folgenden Gleichung berechnet:

$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$



Während im Dieselmotor-Zyklus wird die Effizienz basierend auf der Temperatur mit der folgenden Gleichung berechnet:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

Die Einbeziehung des Faktors $1/\kappa \sim 0,71$ im Dieselmotor-Zyklus macht ihn im Vergleich zum Otto-Zyklus bei der gleichen Temperatureinstellung effizienter. Dies ist eine direkte Folge der Vergrößerung der eingeschlossenen Fläche in der Kurve, die den Zyklus in der Druck-Volumen-Darstellung darstellt.

ID:(11153, 0)


Adiabatische Expansion
Konzept

Angesichts dessen, dass sich ein Gas bei einer adiabatischen Expansion an die Beziehungen der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) hält, wie folgt ausgedrückt:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$



Können wir feststellen, dass während des Zustandswechsels von der Mittleres Volumen ($V_3$) und die Temperatur im Zustand 3 ($T_3$) zu der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 4 ($T_4$) die folgende Gleichheit gilt:

$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$



Unter Verwendung der Gleichung für der Erweiterbarkeitsfaktor ($r_E$):

$ r_E =\displaystyle\frac{ V_1 }{ V_3 }$



Erhalten wir:

$ T_3 = T_4 r_E ^{ \kappa - 1}$

ID:(15751, 0)


Adiabatische Kompression
Konzept

Angesichts dessen, dass in einer adiabatischen Expansion das Gas den Beziehungen der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) entspricht, wie ausgedrückt in:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$



Können wir feststellen, dass während des Zustandswechsels von der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 1 ($T_1$) zu der Komprimiertes Volumen ($V_2$) und die Temperatur im Zustand 2 ($T_2$) die folgende Gleichheit gilt:

$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$



Unter Verwendung der Gleichung für der Kompressibilitätsfaktor ($r_C$):

$ r_C =\displaystyle\frac{ V_1 }{ V_2 }$



Erhalten wir:

$ T_2 = T_1 r_C ^{ \kappa - 1}$

ID:(15752, 0)


Gaserwärmung
Konzept

Da die Erwärmung bei konstantem Druck stattfindet, gilt das Gesetz von Charles:

$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$



Daher muss der Zustandswechsel ($V_2, T_2$) zu ($V_3, T_3$) erfüllen:

$\displaystyle\frac{T_2}{V_2} = \displaystyle\frac{T_3}{V_3}$



Mit den Gleichungen:

$ r_C =\displaystyle\frac{ V_1 }{ V_2 }$



$ r_E =\displaystyle\frac{ V_1 }{ V_3 }$



können wir es umschreiben als:

$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$



Mit anderen Worten:

$ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $

ID:(15753, 0)


Wirkungsgrad in Abhängigkeit von den Temperaturen
Konzept

Die Effizienz in Bezug auf die Temperatur ergibt sich aus der Definition der Effizienz:

$ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $



und den zugeführten Wärmemengen und aufgenommenen Wärmemengen:

$ Q_H = C_p ( T_3 - T_2 )$



$ Q_C = C_V ( T_4 - T_1 )$



Dies führt uns zur Beziehung der Effizienz in Bezug auf die Temperatur:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

ID:(15754, 0)


Effizienz basierend auf Kompressions- und Expansionsfaktoren
Konzept

Der Wert von die Leistungsfähigkeit ($\eta$) kann mithilfe der Werte der Adiabatischer Index ($\kappa$), die Temperatur im Zustand 1 ($T_1$), die Temperatur im Zustand 2 ($T_2$), die Temperatur im Zustand 3 ($T_3$) und die Temperatur im Zustand 4 ($T_4$) in der folgenden Gleichung berechnet werden:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$



Darüber hinaus sind die Beziehungen zwischen den Temperaturen mit der Kompressibilitätsfaktor ($r_C$) und der Erweiterbarkeitsfaktor ($r_E$) durch die folgenden Gleichungen definiert:

$ T_2 = T_1 r_C ^{ \kappa - 1}$



$ T_3 = T_4 r_E ^{ \kappa - 1}$



$ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $



Zusätzlich wird der Wert von der Adiabatischer Index ($\kappa$) in der Gleichung verwendet:

$ \kappa =\displaystyle\frac{ C_p }{ C_V }$



Diese Gleichungen ermöglichen es uns, die Leistung eines Prozesses, der dem Diesel-Zyklus folgt, mithilfe der folgenden Gleichung zu berechnen:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ r_E ^{- \kappa }- r_C ^{- \kappa }}{ r_E ^{-1}- r_C ^{-1}}$

ID:(15755, 0)


Modell
Konzept


ID:(15342, 0)


Der Diesel-Zyklus
Beschreibung

Der Dieseltakt entspricht einem Verbrennungsmotor, bei dem die Erwärmung bei konstantem Druck erfolgt und sich das Gas bei der Zündung des Gemisches ausdehnt.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$Q_C$
Q_C
Absorbierte Wärme
J
$\kappa$
kappa
Adiabatischer Index
-
$r_E$
r_E
Erweiterbarkeitsfaktor
-
$V_1$
V_1
Erweitertes Volumen
m^3
$r_C$
r_C
Kompressibilitätsfaktor
-
$V_2$
V_2
Komprimiertes Volumen
m^3
$\eta$
eta
Leistungsfähigkeit
-
$M$
M
Masse
kg
$V_3$
V_3
Mittleres Volumen
m^3
$c_p$
c_p
Spezifische Wärme bei konstantem Druck
J/kg K
$c_V$
c_V
Spezifische Wärme von Gasen bei konstantem Volumen
J/kg K
$T_1$
T_1
Temperatur im Zustand 1
K
$T_2$
T_2
Temperatur im Zustand 2
K
$T_3$
T_3
Temperatur im Zustand 3
K
$T_4$
T_4
Temperatur im Zustand 4
K
$Q_H$
Q_H
Wärme zugeführt
J
$C_p$
C_p
Wärmekapazität bei konstantem Druck
J/kg
$C_V$
C_V
Wärmekapazität bei konstantem Volumen
J/kg

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Folgend einer Analogie zum ERROR:5219,0 f r Fl ssigkeiten und Feststoffe mit die Wärmekapazität ($C$) und die Masse ($M$):

$ c =\displaystyle\frac{ C }{ M }$



gibt es auch ein Spezifische Wärme von Gasen bei konstantem Volumen ($c_V$) f r das Erhitzen bei konstantem Volumen mit die Wärmekapazität bei konstantem Volumen ($C_V$):

$ c_V =\displaystyle\frac{ C_V }{ M }$

(ID 11113)

In Anlehnung an die Analogie zum ERROR:5219,0 f r Fl ssigkeiten und Feststoffe mit die Wärmekapazität ($C$) und die Masse ($M$):

$ c =\displaystyle\frac{ C }{ M }$



gibt es auch ein Spezifische Wärme bei konstantem Druck ($c_p$) f r das Erw rmen bei konstantem Druck mit die Wärmekapazität bei konstantem Druck ($C_p$):

$ c_p =\displaystyle\frac{ C_p }{ M }$

(ID 11114)

Wenn der Wärme zugeführt ($Q_H$) zugef hrt wird, steigt die Gas temperatur von $T_2$ auf $T_3$ in einem isobaren Prozess (bei konstantem Druck). Dies impliziert, dass wir die Beziehung f r ERROR:8085 mit die Wärmekapazität bei konstantem Druck ($C_p$) und die Variación de Temperature ($\Delta T$) verwenden k nnen, die durch die Gleichung ausgedr ckt wird:

$ \Delta Q = C_p \Delta T $



Dies f hrt uns zu den Werten von die Temperatur im Zustand 3 ($T_3$) und die Temperatur im Zustand 2 ($T_2$) unter Verwendung der Formel:

$ Q_H = C_p ( T_3 - T_2 )$

(ID 11144)

Beim Entfernen von der Absorbierte Wärme ($Q_C$) steigt die Temperatur des Gases von $T_1$ auf $T_4$ in einem isobaren Prozess (bei konstantem Druck). Dies impliziert, dass wir die Beziehung f r ERROR:8085 mit die Wärmekapazität bei konstantem Volumen ($C_V$) und die Variación de Temperature ($\Delta T$) verwenden k nnen, die durch die Gleichung ausgedr ckt wird:

$ dU = C_V \Delta T $



Dies f hrt uns zu den Werten von die Temperatur im Zustand 1 ($T_1$) und die Temperatur im Zustand 4 ($T_4$) mittels der Formel:

$ Q_C = C_V ( T_4 - T_1 )$

(ID 11145)

Angesichts dessen, dass in einer adiabatischen Expansion das Gas den Beziehungen der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) entspricht, wie ausgedr ckt in:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$



K nnen wir feststellen, dass w hrend des Zustandswechsels von der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 1 ($T_1$) zu der Komprimiertes Volumen ($V_2$) und die Temperatur im Zustand 2 ($T_2$) die folgende Gleichheit gilt:

$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$



Unter Verwendung der Gleichung f r der Kompressibilitätsfaktor ($r_C$):

$ r_C =\displaystyle\frac{ V_1 }{ V_2 }$



Erhalten wir:

$ T_2 = T_1 r_C ^{ \kappa - 1}$

(ID 11148)

Angesichts dessen, dass sich ein Gas bei einer adiabatischen Expansion an die Beziehungen der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) h lt, wie folgt ausgedr ckt:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$



K nnen wir feststellen, dass w hrend des Zustandswechsels von der Mittleres Volumen ($V_3$) und die Temperatur im Zustand 3 ($T_3$) zu der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 4 ($T_4$) die folgende Gleichheit gilt:

$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$



Unter Verwendung der Gleichung f r der Erweiterbarkeitsfaktor ($r_E$):

$ r_E =\displaystyle\frac{ V_1 }{ V_3 }$



Erhalten wir:

$ T_3 = T_4 r_E ^{ \kappa - 1}$

(ID 11149)

Da die Erw rmung bei konstantem Druck stattfindet, gilt das Gesetz von Charles:

$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$



Daher muss der Zustandswechsel ($V_2, T_2$) zu ($V_3, T_3$) erf llen:

$\displaystyle\frac{T_2}{V_2} = \displaystyle\frac{T_3}{V_3}$



Mit den Gleichungen:

$ r_C =\displaystyle\frac{ V_1 }{ V_2 }$



$ r_E =\displaystyle\frac{ V_1 }{ V_3 }$



k nnen wir es umschreiben als:

$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$



Mit anderen Worten:

$ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $

(ID 11150)

Der Wert von die Leistungsfähigkeit ($\eta$) kann mithilfe der Werte der Adiabatischer Index ($\kappa$), die Temperatur im Zustand 1 ($T_1$), die Temperatur im Zustand 2 ($T_2$), die Temperatur im Zustand 3 ($T_3$) und die Temperatur im Zustand 4 ($T_4$) in der folgenden Gleichung berechnet werden:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$



Dar ber hinaus sind die Beziehungen zwischen den Temperaturen mit der Kompressibilitätsfaktor ($r_C$) und der Erweiterbarkeitsfaktor ($r_E$) durch die folgenden Gleichungen definiert:

$ T_2 = T_1 r_C ^{ \kappa - 1}$



$ T_3 = T_4 r_E ^{ \kappa - 1}$



$ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $



Zus tzlich wird der Wert von der Adiabatischer Index ($\kappa$) in der Gleichung verwendet:

$ \kappa =\displaystyle\frac{ C_p }{ C_V }$



Diese Gleichungen erm glichen es uns, die Leistung eines Prozesses, der dem Diesel-Zyklus folgt, mithilfe der folgenden Gleichung zu berechnen:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ r_E ^{- \kappa }- r_C ^{- \kappa }}{ r_E ^{-1}- r_C ^{-1}}$

(ID 11156)

Bei einer adiabatischen Expansion erf llt das Gas die Beziehung, die der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$) einschlie t:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$



In diesem Fall vom Anfangspunkt 3 zum Punkt 4. Das bedeutet, dass w hrend der adiabatischen Expansion der Zustand des Gases von der Komprimiertes Volumen ($V_2$) und die Temperatur im Zustand 3 ($T_3$) zu der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 4 ($T_4$) wechselt, gem :

$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$

(ID 11159)

Angesichts dessen, dass bei einer adiabatischen Expansion das Gas die Beziehung zu der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$) erf llt:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$



In diesem Fall, vom anf nglichen Punkt 1 zum Punkt 2. Dies bedeutet, dass w hrend der adiabatischen Kompression der Zustand des Gases von der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 1 ($T_1$) zu der Komprimiertes Volumen ($V_2$) und die Temperatur im Zustand 2 ($T_2$) wie folgt ver ndert wird:

$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$

(ID 11160)

Die Effizienz in Bezug auf die Temperatur ergibt sich aus der Definition der Effizienz:

$ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $



und den zugef hrten W rmemengen und aufgenommenen W rmemengen:

$ Q_H = C_p ( T_3 - T_2 )$



$ Q_C = C_V ( T_4 - T_1 )$



Dies f hrt uns zur Beziehung der Effizienz in Bezug auf die Temperatur:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

(ID 11164)

Beispiele

Der Dieselzyklus ist ein thermodynamischer Kreislauf, der die Grundlage f r Dieselmotoren bildet, die h ufig in Fahrzeugen und Industriemaschinen verwendet werden. Entwickelt von Rudolf Diesel in den 1890er Jahren, unterscheidet sich dieser Zyklus haupts chlich in seinem Z ndprozess vom Otto-Zyklus der Benzinmotoren. Im Dieselzyklus wird Luft in den Zylinder gezogen und zu einem viel h heren Verh ltnis als bei Benzinmotoren komprimiert, was ihre Temperatur so weit erh ht, dass Dieselkraftstoff ohne Z ndkerze entz ndet werden kann.

W hrend des Betriebs beginnt der Zyklus mit dem Einziehen von Luft durch den nach unten bewegenden Kolben. Die Luft wird dann beim Aufw rtshub komprimiert, wodurch ihre Temperatur steigt. Auf dem H hepunkt der Kompressionsphase wird Kraftstoff als feiner Nebel in die hei e komprimierte Luft eingespritzt, was zu einer spontanen Z ndung f hrt. Die Verbrennung treibt den Kolben nach unten und erzeugt so Energie. Schlie lich werden die Verbrennungsgase in der Aussto phase ausgesto en, wenn der Kolben wieder nach oben bewegt wird und den Zyklus abschlie t.

Dieselmotoren sind f r ihre Effizienz und Langlebigkeit bekannt. Das hohe Kompressionsverh ltnis erm glicht es nicht nur, mehr Energie aus dem Kraftstoff zu extrahieren, sondern erh ht auch die thermische Effizienz, was bedeutet, dass ein gr erer Anteil der Energie des Kraftstoffs in mechanische Arbeit umgewandelt wird. Dieselmotoren bieten in der Regel eine bessere Kraftstoffeffizienz und produzieren weniger CO2-Emissionen pro Energieeinheit als ihre Benzin-Gegenst cke, k nnen jedoch h here Emissionen anderer Schadstoffe wie Stickoxide und Partikel emittieren.

(ID 15283)

Sadi Carnot f hrte [1] das theoretische Konzept der ersten Maschinenkonstruktion ein, die auf einem Temperaturgradienten basierend mechanische Arbeit erzeugen kann. Dies wird durch einen Prozess im Druck-Volumen-Raum erreicht, bei dem W rme hinzugef gt und extrahiert wird, wie in der Abbildung dargestellt:



Die Fl che unter der Kurve der Wärme zugeführt ($Q_H$), die von 1 bis 2 reicht, repr sentiert die erforderliche Energiezufuhr, um vom Zustand ($p_1, V_1$) zum Zustand ($p_2, V_2$) berzugehen. Umgekehrt repr sentiert die Fl che unter der Kurve der Absorbierte Wärme ($Q_C$), die von 2 bis 1 verl uft, die ben tigte Energieentnahme, um vom Zustand ($p_2, V_2$) zur ck zum Zustand ($p_1, V_1$) zu gelangen. Die Differenz zwischen diesen Fl chen entspricht dem von beiden Kurven umschlossenen Bereich und repr sentiert der Effektive Arbeit ($W$), den das System ausf hren kann.

Carnot zeigte auch, dass gem dem zweiten Hauptsatz der Thermodynamik der Wärme zugeführt ($Q_H$) nicht null sein kann. Dies impliziert, dass es keine Maschinen gibt, die in der Lage sind, die gesamte W rme in Arbeit umzuwandeln. [1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflexionen ber die Triebkraft des Feuers und ber Maschinen zur Entwicklung dieser Triebkraft), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, S. 393-457 (1872)

(ID 11131)

Rudolf Diesel [1] hatte das Ziel, einen Zyklus zu entwickeln, der sich vom Carnot-Zyklus unterscheidet und eine h here Effizienz im Vergleich zum Otto-Zyklus erreicht. Dieser Prozess verl uft in den folgenden Stufen:

• Stufe 1 bis 2: Adiabatische Verdichtung $(p_1,V_1,T_1)\rightarrow (p_2,V_2,T_2)$,
• Stufe 2 bis 3: Erw rmung und Expansion bei konstantem Druck $(p_2,V_2,T_2)\rightarrow (p_2,V_3,T_3)$,
• Stufe 3 bis 4: Adiabatische Expansion $(p_2,V_3,T_3)\rightarrow (p_3,V_1,T_4)$,
• Stufe 4 bis 1: Abk hlung bei konstantem Volumen $(p_3,V_1,T_4)\rightarrow (p_1,V_1,T_1)$

Diese Stufen sind nachfolgend dargestellt:

Der Schl ssel liegt in Stufe 2 bis 3, wo die Expansion bei konstantem Druck erfolgt. Der Grund wird deutlich, wenn man sich das Diagramm ansieht:

Die gewonnene Energie entspricht der Fl che innerhalb des Zyklus, und durch die Kompression bei konstantem Druck ist diese Fl che gr er als im Fall der Kompression bei konstantem Volumen. [1] "Verfahren zur Entwickelung eines rationellen W rmemotors zum Ersatz der Dampfmaschine und der heute bekannten Verbrennungsmotoren" (Verfahren zur Entwicklung eines rationalen W rmemotors zur Ersetzung der Dampfmaschine und der heutigen bekannten Verbrennungsmotoren), Rudolf Diesel, Kaiserlichen Patentamts, Nr. 67207 (1892)

(ID 11141)

Sowohl der Otto-Zyklus als auch der Dieselmotor-Zyklus sind abh ngig von den Variablen die Temperatur im Zustand 1 ($T_1$), die Temperatur im Zustand 2 ($T_2$), die Temperatur im Zustand 3 ($T_3$) und die Temperatur im Zustand 4 ($T_4$). Im Falle des Dieselmotor-Zyklus h ngt er auch von der Adiabatischer Index ($\kappa$) ab, dessen Wert 1,4 betr gt.

Im Otto-Zyklus wird die Effizienz basierend auf der Temperatur mit der folgenden Gleichung berechnet:

$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$



W hrend im Dieselmotor-Zyklus wird die Effizienz basierend auf der Temperatur mit der folgenden Gleichung berechnet:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

Die Einbeziehung des Faktors $1/\kappa \sim 0,71$ im Dieselmotor-Zyklus macht ihn im Vergleich zum Otto-Zyklus bei der gleichen Temperatureinstellung effizienter. Dies ist eine direkte Folge der Vergr erung der eingeschlossenen Fl che in der Kurve, die den Zyklus in der Druck-Volumen-Darstellung darstellt.

(ID 11153)

Angesichts dessen, dass sich ein Gas bei einer adiabatischen Expansion an die Beziehungen der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) h lt, wie folgt ausgedr ckt:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$



K nnen wir feststellen, dass w hrend des Zustandswechsels von der Mittleres Volumen ($V_3$) und die Temperatur im Zustand 3 ($T_3$) zu der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 4 ($T_4$) die folgende Gleichheit gilt:

$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$



Unter Verwendung der Gleichung f r der Erweiterbarkeitsfaktor ($r_E$):

$ r_E =\displaystyle\frac{ V_1 }{ V_3 }$



Erhalten wir:

$ T_3 = T_4 r_E ^{ \kappa - 1}$

(ID 15751)

Angesichts dessen, dass in einer adiabatischen Expansion das Gas den Beziehungen der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$), die Temperatur im Endzustand ($T_f$) und der Adiabatischer Index ($\kappa$) entspricht, wie ausgedr ckt in:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$



K nnen wir feststellen, dass w hrend des Zustandswechsels von der Erweitertes Volumen ($V_1$) und die Temperatur im Zustand 1 ($T_1$) zu der Komprimiertes Volumen ($V_2$) und die Temperatur im Zustand 2 ($T_2$) die folgende Gleichheit gilt:

$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$



Unter Verwendung der Gleichung f r der Kompressibilitätsfaktor ($r_C$):

$ r_C =\displaystyle\frac{ V_1 }{ V_2 }$



Erhalten wir:

$ T_2 = T_1 r_C ^{ \kappa - 1}$

(ID 15752)

Da die Erw rmung bei konstantem Druck stattfindet, gilt das Gesetz von Charles:

$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$



Daher muss der Zustandswechsel ($V_2, T_2$) zu ($V_3, T_3$) erf llen:

$\displaystyle\frac{T_2}{V_2} = \displaystyle\frac{T_3}{V_3}$



Mit den Gleichungen:

$ r_C =\displaystyle\frac{ V_1 }{ V_2 }$



$ r_E =\displaystyle\frac{ V_1 }{ V_3 }$



k nnen wir es umschreiben als:

$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$



Mit anderen Worten:

$ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $

(ID 15753)

Die Effizienz in Bezug auf die Temperatur ergibt sich aus der Definition der Effizienz:

$ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $



und den zugef hrten W rmemengen und aufgenommenen W rmemengen:

$ Q_H = C_p ( T_3 - T_2 )$



$ Q_C = C_V ( T_4 - T_1 )$



Dies f hrt uns zur Beziehung der Effizienz in Bezug auf die Temperatur:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

(ID 15754)

Der Wert von die Leistungsfähigkeit ($\eta$) kann mithilfe der Werte der Adiabatischer Index ($\kappa$), die Temperatur im Zustand 1 ($T_1$), die Temperatur im Zustand 2 ($T_2$), die Temperatur im Zustand 3 ($T_3$) und die Temperatur im Zustand 4 ($T_4$) in der folgenden Gleichung berechnet werden:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$



Dar ber hinaus sind die Beziehungen zwischen den Temperaturen mit der Kompressibilitätsfaktor ($r_C$) und der Erweiterbarkeitsfaktor ($r_E$) durch die folgenden Gleichungen definiert:

$ T_2 = T_1 r_C ^{ \kappa - 1}$



$ T_3 = T_4 r_E ^{ \kappa - 1}$



$ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $



Zus tzlich wird der Wert von der Adiabatischer Index ($\kappa$) in der Gleichung verwendet:

$ \kappa =\displaystyle\frac{ C_p }{ C_V }$



Diese Gleichungen erm glichen es uns, die Leistung eines Prozesses, der dem Diesel-Zyklus folgt, mithilfe der folgenden Gleichung zu berechnen:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ r_E ^{- \kappa }- r_C ^{- \kappa }}{ r_E ^{-1}- r_C ^{-1}}$

(ID 15755)


(ID 15342)

ID:(1487, 0)