Usuario:
Maquinas Termodinámicas
Storyboard 
La maquina termodinámica fue primero analizada por Sadi Carnot que en 1824 publico su 'Reflexiones sur la Puissance Matrice du Feu sur les Machines' analiza como el calor se puede emplear para realizar trabajo. En principio es la aplicación de la primera ley de la termodinámica en que un sistema en un sistema circula calor de modo de que una fracción se convierte en trabajo. La fracción se denomina la eficiencia de la maquina y por la segunda ley de la termodinámica esta limitada no pudiendo convertirse todo el calor en trabajo.
ID:(1484, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \delta W = p dV $
dW = p * dV
$ W = ( T_H - T_C )( S_H - S_C )$
W =( T_H - T_C )*( S_H - S_C )
$\displaystyle\oint_C p\,dV=\displaystyle\int_{V_1}^{V_2}p_{dir}\,dV-\displaystyle\int_{V_1}^{V_2}p_{inv}\,dV$
int_V1^V2 pdV
$\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$
int_V2^V1 p_inv dV=-int_V1^V2 p_inv dV
ID:(15339, 0)
Representación gráfica del trabajo a ser invertido
Imagen
Para repetir el proceso, es necesario volver del volumen $V_2$ al volumen $V_1$, lo que implica seguir una curva en el diagrama de presión versus volumen en sentido contrario:
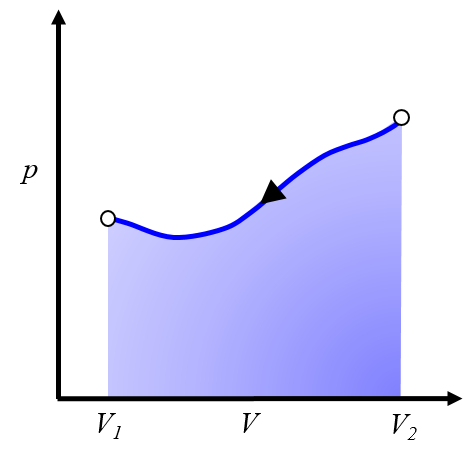
Esto representa un trabajo que debe ser invertido y que debemos suministrar para poder repetir el ciclo.
Por lo general, este proceso se logra enfriando el sistema, lo que provoca su contracción. La energía que debemos invertir corresponde al calor retirado del sistema.
ID:(10254, 0)
Representación gráfica del trabajo efectivo obtenido
Imagen
El trabajo neto obtenido es la diferencia entre el trabajo obtenido y el trabajo necesario para completar el ciclo:
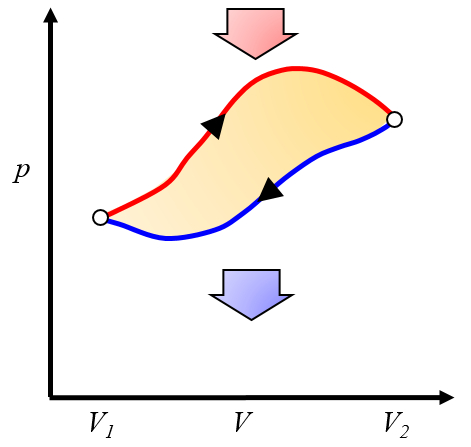
ID:(10268, 0)
Representación gráfica del trabajo obtenido
Imagen
Dado que el trabajo es
| $ \delta W = p dV $ |
se puede representar en un gráfico de presión versus volumen como el área debajo de la curva de presión en función del volumen:
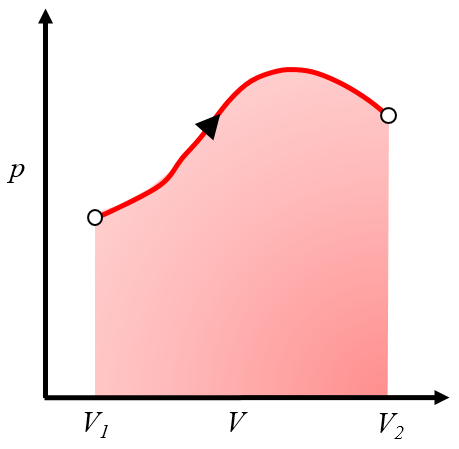
Este área representa el trabajo obtenido cuando un gas realiza trabajo al expandirse desde el volumen $V_1$ al volumen $V_2$.
Normalmente, este proceso se logra calentando el sistema, lo que provoca la expansión y realiza el trabajo. Un ejemplo sería un pistón con gas calentado en una caldera.
ID:(10266, 0)
Trabajo a invertir
Ecuación
Al contraer el volumen desde $V_2$ a $V_1$, es necesario suministrar energía a la máquina, representada por
| $\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$ |
La necesidad de suministrar esta energía se refleja en el signo del integral.
ID:(10255, 0)
Trabajo en el modelo simplificado
Ecuación
La integral en el modelo simplificado,
| $ W =\displaystyle\oint_C T dS $ |
puede estimarse de manera sencilla utilizando la fórmula de área, multiplicando la altura por la base del área que representa el trabajo:
| $ W = ( T_H - T_C )( S_H - S_C )$ |
ID:(10261, 0)
Trabajo total
Ecuación
El trabajo total se calcula integrando sobre el ciclo completo, es decir, la parte en la que se realiza trabajo
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
y la parte en la que se invierte el proceso
| $\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$ |
que se convierte en una resta. Este proceso cíclico se representa matemáticamente mediante una integral con un círculo y corresponde a la suma de los elementos debajo de la curva en cada etapa:
| $\displaystyle\oint_C p\,dV=\displaystyle\int_{V_1}^{V_2}p_{dir}\,dV-\displaystyle\int_{V_1}^{V_2}p_{inv}\,dV$ |
ID:(10256, 0)
Presión y trabajo
Ecuación
El diferencial inexacto del trabajo ($\delta W$) es igual a la presión ($p$) multiplicado por la variación del volumen ($dV$):
| $ \delta W = p dV $ |
Dado que la fuerza mecánica ($F$) dividida por la sección ($S$) es igual a la presión ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
y la variación del volumen ($dV$) con el camino recorrido ($dx$) es igual a:
| $ \Delta V = S \Delta s $ |
La ecuación para el diferencial inexacto del trabajo ($\delta W$) se puede expresar como:
| $ \delta W = F dx $ |
Así que puede ser escrita como:
| $ \delta W = p dV $ |
ID:(3468, 0)
Ciclo de Carnot: esquema de una maquina
Concepto
En una máquina que utiliza el concepto de Carnot, se llevan a cabo los siguientes procesos:
• El reservorio con la temperatura más alta se crea mediante un horno.
• El reservorio con la temperatura más baja se crea mediante un sistema de refrigeración.
• El vapor generado desde el reservorio se expande en forma de gas, desplazando el pistón y elevando la masa de compensación. En la primera etapa isotérmica, la primera válvula está abierta mientras que la segunda está cerrada. En la segunda etapa del proceso, se cierra la primera válvula y la expansión continúa de manera adiabática.
• En la tercera etapa, se abre la segunda válvula y con ayuda de la masa de compensación, el pistón regresa y el gas es expulsado de forma isotérmica. En la cuarta etapa, se cierra la válvula y el proceso concluye de manera adiabática.
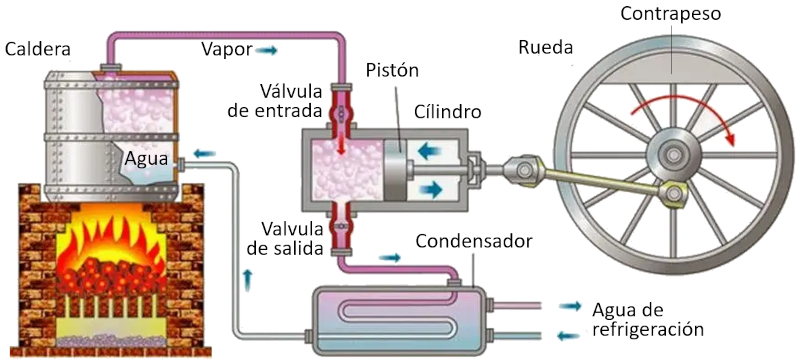
ID:(11134, 0)
Ciclo de Carnot
Concepto
Sadi Carnot introduced [1] the theoretical concept of the first machine design that, based on a heat gradient, can generate mechanical work. This is achieved through a process in the pressure-volume space where heat is added and extracted, as illustrated in the image:
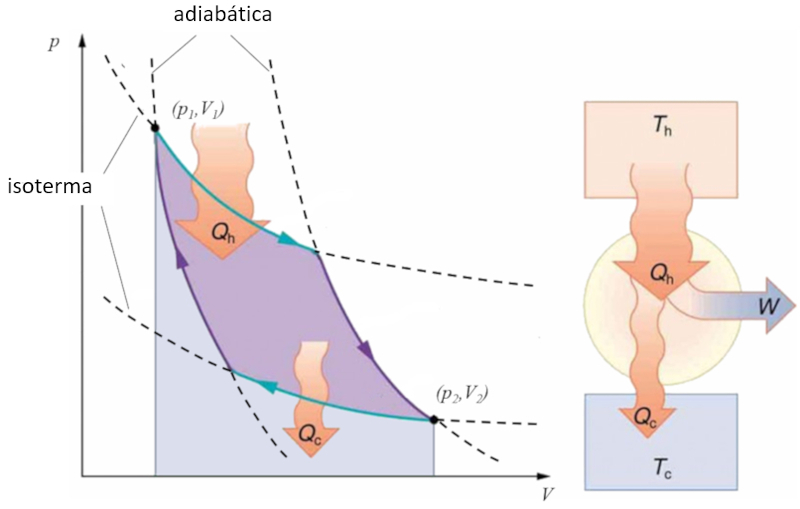
The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.
Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las máquinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
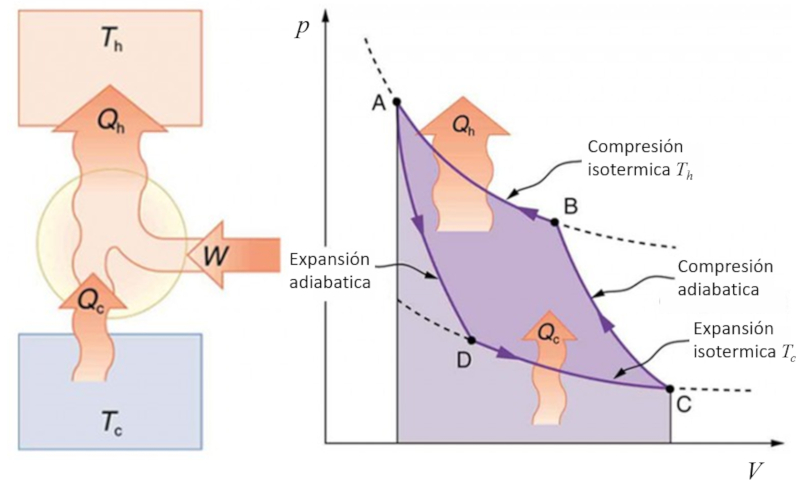
Ciclo de Carnot para refrigeración
Descripción
Si invertimos el proceso de Carnot, podemos utilizar trabajo para transferir calor, lo cual se conoce como una bomba de calor. En este caso, el diagrama se representa de la siguiente manera:
ID:(11143, 0)