Utilizador:
Modelo
Top 
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ \delta W = p dV $
dW = p * dV
$ W = ( T_H - T_C )( S_H - S_C )$
W =( T_H - T_C )*( S_H - S_C )
$\displaystyle\oint_C p\,dV=\displaystyle\int_{V_1}^{V_2}p_{dir}\,dV-\displaystyle\int_{V_1}^{V_2}p_{inv}\,dV$
int_V1^V2 pdV
$\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$
int_V2^V1 p_inv dV=-int_V1^V2 p_inv dV
ID:(15339, 0)
Representação gráfica da obra a ser investida
Imagem
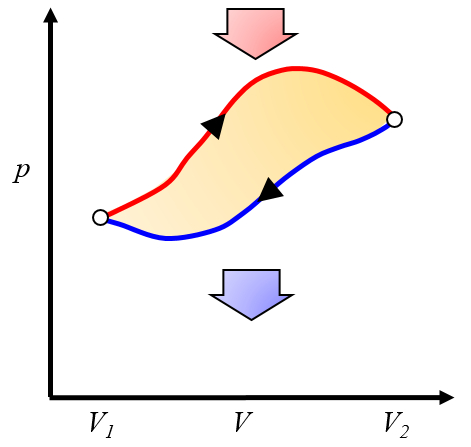
Para repetir o processo, é necessário retornar do volume $V_2$ para o volume $V_1$, o que implica seguir uma curva no diagrama de pressão versus volume na direção oposta:
Isso representa um trabalho a ser realizado e que devemos fornecer para repetir o ciclo.
Normalmente, esse processo é alcançado resfriando o sistema, o que faz com que ele se contraia. A energia a ser investida corresponde ao calor retirado do sistema.
ID:(10254, 0)
Representação gráfica do trabalho efetivo obtido
Imagem
O trabalho líquido obtido é a diferença entre o trabalho obtido e o trabalho necessário para completar o ciclo:
ID:(10268, 0)
Representação gráfica do trabalho obtido
Imagem
Uma vez que o trabalho é
| $ \delta W = p dV $ |
ele pode ser representado em um gráfico de pressão versus volume como a área sob a curva de pressão em função do volume:
Essa área representa o trabalho obtido quando um gás realiza trabalho ao expandir-se do volume $V_1$ para o volume $V_2$.
Normalmente, esse processo é alcançado aquecendo o sistema, o que faz com que ele se expanda e realize o trabalho. Um exemplo seria um pistão com gás aquecido em uma caldeira.
ID:(10266, 0)
Trabalhe no modelo simplificado
Equação
A integral no modelo simplificado,
| $ W =\displaystyle\oint_C T dS $ |
pode ser estimada facilmente usando a fórmula de área, multiplicando a altura pela base da área que representa o trabalho:
| $ W = ( T_H - T_C )( S_H - S_C )$ |
ID:(10261, 0)
Trabalhe para investir
Equação
Ao contrair o volume de $V_2$ para $V_1$, é necessário fornecer energia à máquina, representada por
| $\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$ |
A necessidade de fornecer essa energia é refletida no sinal do integral.
ID:(10255, 0)
Trabalho total
Equação
O trabalho total é calculado integrando sobre o ciclo completo, ou seja, a parte em que o trabalho é realizado
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
e a parte em que o processo é revertido
| $\displaystyle\int_{V_2}^{V_1}p_{inv}dV=-\displaystyle\int_{V_1}^{V_2}p_{inv}dV$ |
resultando em uma subtração. Esse processo cíclico é representado matematicamente como uma integral com um círculo e corresponde à soma dos elementos sob a curva em cada etapa:
| $\displaystyle\oint_C p\,dV=\displaystyle\int_{V_1}^{V_2}p_{dir}\,dV-\displaystyle\int_{V_1}^{V_2}p_{inv}\,dV$ |
ID:(10256, 0)
Pressão e trabalho
Equação
O diferencial de trabalho impreciso ($\delta W$) é igual a la pressão ($p$) multiplicado por la variação de volume ($dV$):
| $ \delta W = p dV $ |
Uma vez que la força mecânica ($F$) dividido por la seção ($S$) é igual a la pressão ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
e la variação de volume ($dV$) com o distância percorrida ($dx$) é igual a:
| $ \Delta V = S \Delta s $ |
A equação para o diferencial de trabalho impreciso ($\delta W$) pode ser expressa como:
| $ \delta W = F dx $ |
Portanto, ela pode ser escrita como:
| $ \delta W = p dV $ |
ID:(3468, 0)
Ciclo de Carnot: esquema de uma máquina
Conceito
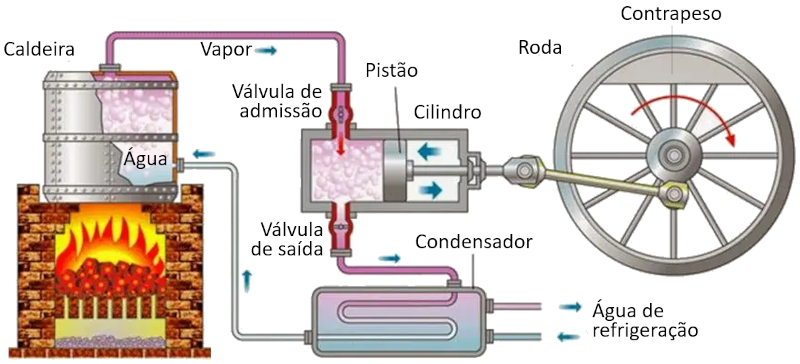
Em uma máquina que utiliza o conceito de Carnot, ocorrem os seguintes processos:
• O reservatório com a temperatura mais alta é criado usando um forno.
• O reservatório com a temperatura mais baixa é criado usando um sistema de refrigeração.
• O vapor gerado a partir do reservatório se expande em forma de gás, deslocando o pistão e elevando a massa de compensação. Na primeira etapa isoterma, a primeira válvula está aberta enquanto a segunda está fechada. Na segunda etapa do processo, a primeira válvula é fechada e a expansão continua adiabaticamente.
• Na terceira etapa, a segunda válvula é aberta e, com a ajuda da massa de compensação, o pistão retorna e o gás é expelido de forma isoterma. Na quarta etapa, a válvula é fechada e o processo é concluído adiabaticamente.
ID:(11134, 0)
Ciclo de Carnot
Conceito
Sadi Carnot introduziu [1] o conceito teórico do primeiro projeto de máquina capaz de gerar trabalho mecânico com base em um gradiente de temperatura. Isso é alcançado por meio de um processo no espaço pressão-volume, onde calor é adicionado e extraído, conforme ilustrado na imagem:
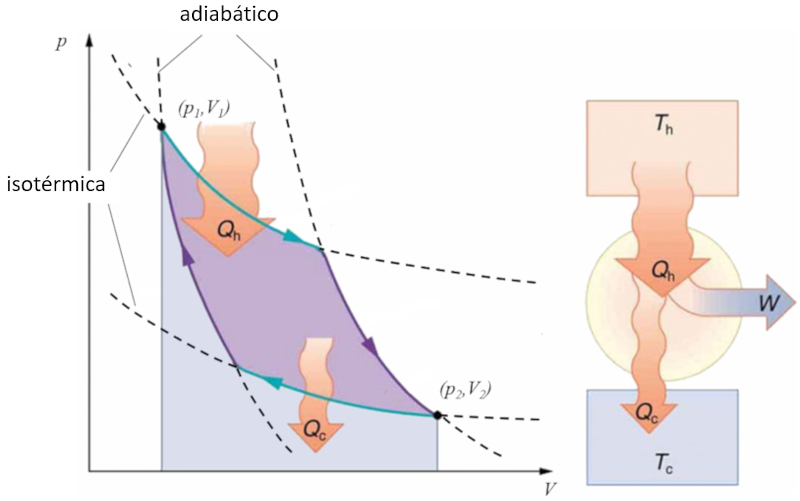
A área sob a curva o calor fornecido ($Q_H$), que se estende de 1 a 2, representa a energia necessária para transitar do estado ($p_1, V_1$) para o estado ($p_2, V_2$). Por outro lado, a área sob a curva o calor absorvido ($Q_C$), indo de 2 para 1, representa a extração de energia necessária para retornar do estado ($p_2, V_2$) ao estado ($p_1, V_1$). A diferença entre essas áreas corresponde à região delimitada por ambas as curvas e representa o trabalho eficaz ($W$) que o sistema pode realizar.
Carnot também demonstrou que, de acordo com a segunda lei da termodinâmica, o calor fornecido ($Q_H$) não pode ser igual a zero. Isso implica que não existem máquinas capazes de converter todo o calor em trabalho.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexões sobre a Potência Motriz do Fogo e sobre Máquinas Adequadas para Desenvolver Essa Potência), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Ciclo de Carnot para refrigeração
Descrição
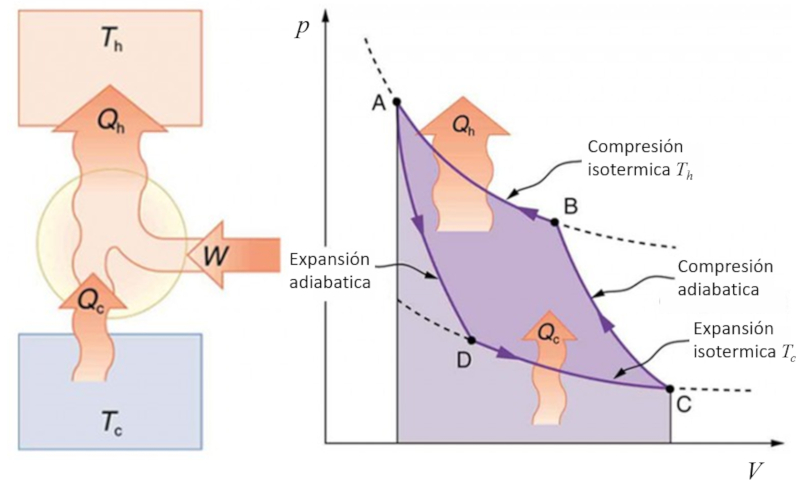
Se o processo de Carnot for invertido, pode-se utilizar trabalho para transferir calor, o que é conhecido como uma bomba de calor. Nesse caso, o diagrama é o seguinte:
ID:(11143, 0)