Außerhalb einer Kugel
Storyboard 
Sowohl für eine leitende Kugel als auch für eine isolierende Kugel hängt das äußere Feld nur von der Gesamtladung ab, unabhängig davon, ob sie sich auf der Oberfläche (leitende Kugel) oder im Inneren (isolierende Kugel) befindet.
ID:(2078, 0)
Außerhalb einer Kugel
Storyboard 
Sowohl für eine leitende Kugel als auch für eine isolierende Kugel hängt das äußere Feld nur von der Gesamtladung ab, unabhängig davon, ob sie sich auf der Oberfläche (leitende Kugel) oder im Inneren (isolierende Kugel) befindet.
Variablen
Berechnungen
Berechnungen
Gleichungen
Im Fall einer kugelf rmigen Gau -Oberfl che ist das elektrische Feld konstant, sodass der Elektrisches Feld ($E$) unter Verwendung von die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Oberfläche der Leiters ($S$) berechnet werden kann, was zu folgendem Ergebnis f hrt:
Da die Oberfläche einer Kugel ($S$) gleich der Pi ($\pi$) und der Scheibenradius ($r$) ist, ergibt sich:
Schlie lich ist der Elektrisches Feld, Kugel, außen ($E_e$) zusammen mit die Entfernung zwischen Ladungen ($r$) gleich:
F r den Fall einer kugelf rmigen Gau -Oberfl che ist das elektrische Feld konstant. Daher ist der Elektrisches Feld ($E$) gleich die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Oberfläche der Leiters ($S$) gem :
Da die Oberfl che von die Oberfläche einer Kugel ($S$) gleich der Pi ($\pi$) und der Scheibenradius ($r$) ist, haben wir:
Die in der Gau -Oberfl che eingeschlossene Ladung, mit die Eingekapselte Ladung auf der Gauß-Oberfläche ($q$), der Kugelradius ($R$) und die Entfernung zwischen Ladungen ($r$), ergibt:
Daher ergibt sich der Elektrisches Feld, Kugel, Innenraum ($E_i$) als:
Da der Potentialunterschied der Elektrisches Potential, isolierende Kugel, innen ($\varphi_i$) mit der Elektrisches Feld, Kugel, Innenraum ($E_i$) und der Radius ($r$) ist, ergibt sich:
Da der Elektrisches Feld, Kugel, Innenraum ($E_i$) mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$), der Kugelradius ($R$) und die Entfernung zwischen Ladungen ($r$) gleich ist:
In sph rischen Koordinaten haben wir:
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
Daher ergibt sich der Elektrisches Potential, isolierende Kugel, innen ($\varphi_i$) mit die Entfernung zwischen Ladungen ($r$) in:
Da der Potentialunterschied der Elektrisches Potential, Kugel, außen ($\varphi_e$) mit der Elektrisches Feld, Kugel, außen ($E_e$), der Elektrisches Feld, Kugel, Innenraum ($E_i$), der Kugelradius ($R$) und der Radius ($r$) ist, ergibt sich:
Da der Elektrisches Feld, Kugel, außen ($E_e$) mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Entfernung zwischen Ladungen ($r$) gleich ist:
und der Elektrisches Feld, Kugel, Innenraum ($E_i$) mit der Inneres Radius ($r_i$) gleich ist:
In sph rischen Koordinaten haben wir:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Daher ergibt sich der Elektrisches Potential, Kugel, außen ($\varphi_e$) in:
Beispiele
Im Fall einer sph rischen Gau 'schen Oberfl che ist der Elektrisches Feld ($\vec{E}$) in Richtung von der Versor normal zum Abschnitt ($\hat{n}$) konstant. Daher kann es unter Verwendung von die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$) und die Dielektrizitätskonstante ($\epsilon$) durch Integration ber die Oberfläche, wo das elektrische Feld konstant ($dS$) berechnet werden:
Da die Oberfl che von die Oberfläche einer Kugel ($S$) gleich der Pi ($\pi$) und der Scheibenradius ($r$) ist, haben wir:
was in der Grafik dargestellt ist
Au erhalb der Kugel ist der Elektrisches Feld, Kugel, außen ($E_e$) mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Entfernung zwischen Ladungen ($r$) gleich:
W hrend im Fall einer isolierenden Kugel der Elektrisches Feld, Kugel, Innenraum ($E_i$) mit der Kugelradius ($R$) gleich ist:
Wenn die Kugel leitend ist, werden sich die Ladungen auf der Oberfl che verteilen, und der Elektrisches Feld, Kugel, Innenraum ($E_i$) wird null sein.
Da der Potentialunterschied der Elektrisches Potential, Kugel, außen ($\varphi_e$) mit der Elektrisches Feld, Kugel, außen ($E_e$), der Elektrisches Feld, Kugel, Innenraum ($E_i$), der Kugelradius ($R$) und der Radius ($r$) ist, ergibt sich:
Da der Elektrisches Feld, Kugel, außen ($E_e$) mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Entfernung zwischen Ladungen ($r$) gleich ist:
und der Elektrisches Feld, Kugel, Innenraum ($E_i$) mit der Inneres Radius ($r_i$) gleich ist:
In sph rischen Koordinaten haben wir:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Daher ergibt sich der Elektrisches Potential, Kugel, außen ($\varphi_e$) in:
Wie in der folgenden Grafik dargestellt:
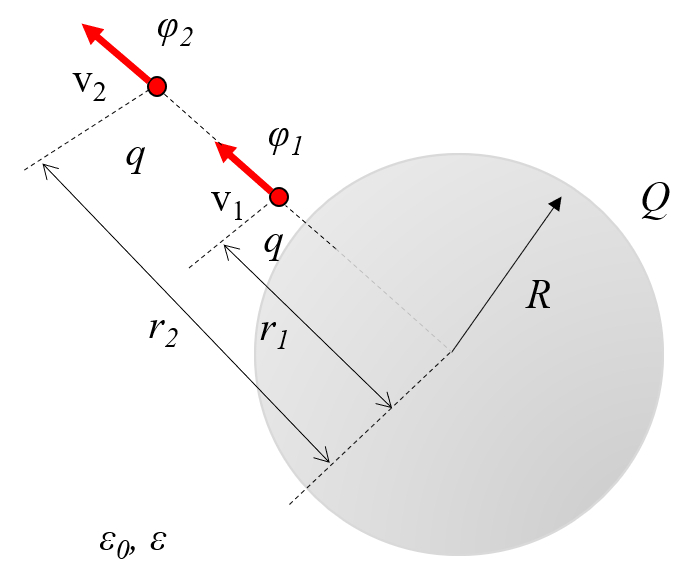
muss das Feld an zwei Punkten die gleiche Energie aufweisen. Daher m ssen die Variablen die Ladung ($Q$), die Partikelmasse ($m$), die Geschwindigkeit 1 ($v_1$), die Geschwindigkeit 2 ($v_2$) und der Elektrisches Potential 1 ($\varphi_1$) gem der Gleichung:
und der Elektrisches Potential 2 ($\varphi_2$) gem der Gleichung:
die folgende Beziehung erf llen:
Der Elektrisches Feld, Kugel, Innenraum ($E_i$) ist mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$), der Kugelradius ($R$) und die Entfernung zwischen Ladungen ($r$) ist gleich:
Der Elektrisches Feld, Kugel, außen ($E_e$) ist mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Entfernung zwischen Ladungen ($r$) ist gleich:
Der Elektrisches Potential, isolierende Kugel, innen ($\varphi_i$) ist mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$), die Entfernung zwischen Ladungen ($r$) und der Kugelradius ($R$) ist gleich:
Der Elektrisches Potential, Kugel, außen ($\varphi_e$) ist mit der Pi ($\pi$), die Ladung ($Q$), die Elektrische Feldkonstante ($\epsilon_0$), die Dielektrizitätskonstante ($\epsilon$) und die Entfernung zwischen Ladungen ($r$) ist gleich:
Elektrische Potentiale, die die potenzielle Energie pro Ladungseinheit darstellen, beeinflussen, wie sich die Geschwindigkeit eines Teilchens ndert. Daher folgt aus der Energieerhaltung zwischen zwei Punkten, dass in Anwesenheit der Variablen die Ladung ($q$), die Partikelmasse ($m$), die Geschwindigkeit 1 ($v_1$), die Geschwindigkeit 2 ($v_2$), der Elektrisches Potential 1 ($\varphi_1$) und der Elektrisches Potential 2 ($\varphi_2$) die folgende Beziehung erf llt sein muss:
ID:(2078, 0)