A plate
Storyboard 
The geometry referred to as a plate can be described as an infinitely large plane that is electrically charged.
Variables
Calculations
Calculations
Equations
According to Gauss's Law, the variables the surface where the electric field is constant ($dS$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the versor normal to the section ($\hat{n}$), and the electric field ($\vec{E}$) satisfy the following equation:
In the case of a flat Gaussian surface, the field must be constant, so the relationship of the electric eield ($E$) with the surface of the conductor ($S$) is established as:
Since the charge density by area ($\sigma$) is equally defined by:
For the electric field of an infinite plate ($E_s$), the resulting expression is:
In the case of an infinite plate, the relationship between the electric potential, infinite plate ($\varphi_s$), the electric field of an infinite plate ($E_s$), and the position on the z axis ($z$) is established by the following equation:
Similarly, the relationship involving the electric field of an infinite plate ($E_s$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the charge density by area ($\sigma$) is defined as:
In spherical coordinates, this is expressed as:
$\varphi_s = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z$
Finally, the relationship that includes the electric potential, infinite plate ($\varphi_s$) and the position on the z axis ($z$) is determined by the following equation:
In the case of an infinite plate, the relationship between the electric potential, infinite plate ($\varphi_s$), the electric field of an infinite plate ($E_s$), and the position on the z axis ($z$) is established by the following equation:
Similarly, the relationship involving the electric field of an infinite plate ($E_s$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the charge density by area ($\sigma$) is defined as:
In spherical coordinates, this is expressed as:
$\varphi_s = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z$
Finally, the relationship that includes the electric potential, infinite plate ($\varphi_s$) and the position on the z axis ($z$) is determined by the following equation:
Examples
According to Gauss's Law, the variables the surface where the electric field is constant ($dS$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the versor normal to the section ($\hat{n}$), and the electric field ($\vec{E}$) satisfy the following equation:
In the case of a flat Gaussian surface, the field must be constant, so the relationship of the electric eield ($E$) with the surface of the conductor ($S$) is established as:
what is shown in the graph
Since the charge density by area ($\sigma$) is equally defined by:
For the electric field of an infinite plate ($E_s$), the resulting expression is:
The reference electrical, two infinity plates ($\varphi_d$) is with the electric field, two infinite plates ($E_d$) and the position on the z axis ($z$) is equal to:
the electric field of an infinite plate ($E_s$) is with the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$) and the charge density by area ($\sigma$) is equal to:
the electric potential, infinite plate ($\varphi_s$) is with and the position on the z axis ($z$) turns out
As illustrated in the following graph:
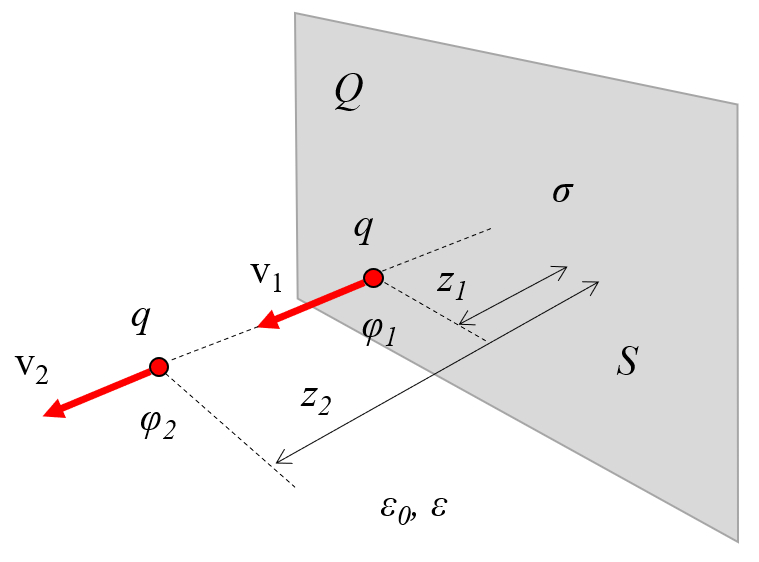
the field at two points must have the same energy. Therefore, the variables the charge ($Q$), the particle mass ($m$), the speed 1 ($v_1$), the speed 2 ($v_2$), and the electric potential 1 ($\varphi_1$) according to the equation:
and the electric potential 2 ($\varphi_2$), according to the equation:
must satisfy the following relationship:
The surface charge density is calculated by dividing the total charge by the surface area. Therefore, the relationship between the charge density by area ($\sigma$) and the charge ($Q$) with the surface of the conductor ($S$) is established as:
The electric field of an infinite plate ($E_s$) is with the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$) and the charge density by area ($\sigma$) equal to:
The electric potential, infinite plate ($\varphi_s$) is with the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the charge density by area ($\sigma$) and the position on the z axis ($z$) is equal to:
The electric potential, infinite plate ($\varphi_s$) is with the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the charge density by area ($\sigma$) and the position on the z axis ($z$) is equal to:
Electric potentials, which represent potential energy per unit of charge, influence how the velocity of a particle varies. Consequently, due to the conservation of energy between two points, it follows that in the presence of variables the charge ($q$), the particle mass ($m$), the speed 1 ($v_1$), the speed 2 ($v_2$), the electric potential 1 ($\varphi_1$), and the electric potential 2 ($\varphi_2$), the following relationship must be satisfied:
ID:(2079, 0)