User:
Resistances
Storyboard 
Resistances are elements that allow the generation of defined currents avoiding direct discharges.
ID:(1585, 0)
Resistances
Description
Resistances are elements that allow the generation of defined currents avoiding direct discharges.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Examples
The resistors are elements in the shape of cylinders and have rings that indicate their values:
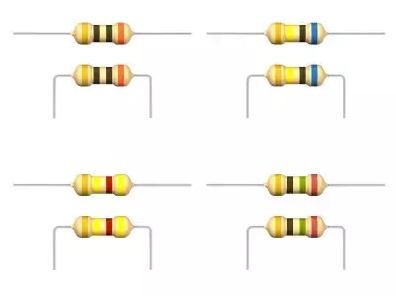
(ID 11762)
The value is coded with colored rings:
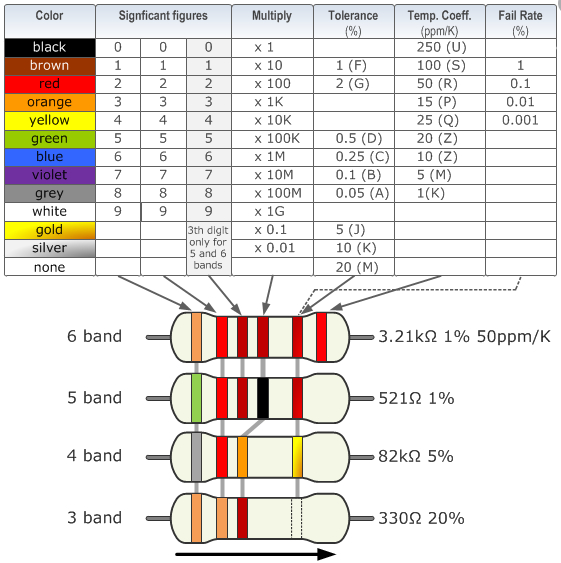
(ID 11763)
There are two symbols depending on the origin of the diagrams. Americans draw the resistors as zigzag lines while in Europe a rectangle is used:
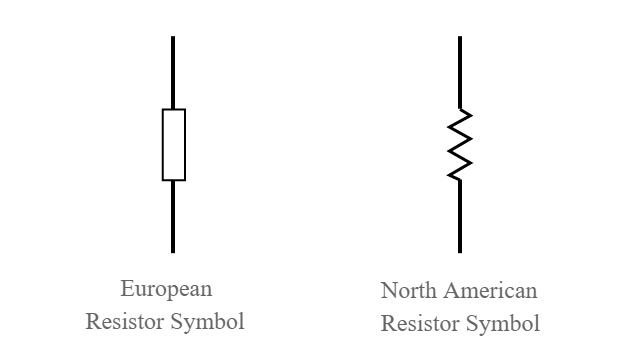
(ID 11764)
Este es un circuito para una sirena. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con n meros)
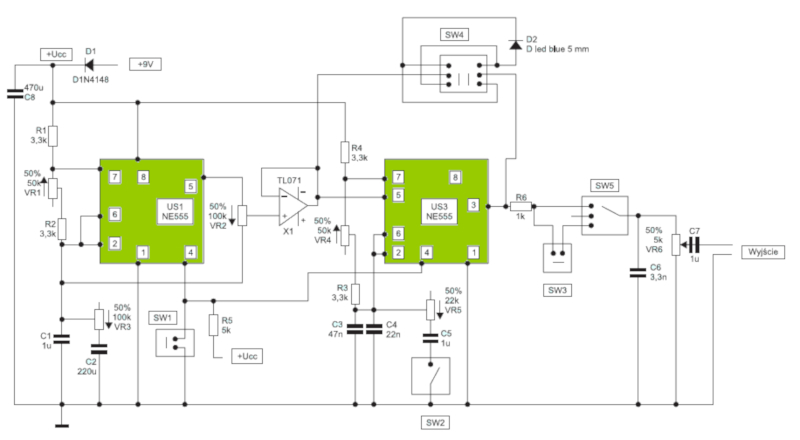
(ID 11704)
Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con m todos fotoquimicos. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• procesadores (cajas rectangulares con n meros)
(ID 11705)
The diagram representing resistors connected in series has the following form:
(ID 7862)
The diagram representing resistors connected in parallel has the following form:
xa0
(ID 7861)
ID:(1585, 0)