Widerstand
Storyboard 
Widerstände sind Elemente, die die Erzeugung definierter Ströme ermöglichen und direkte Entladungen vermeiden.
ID:(1585, 0)
Widerstand
Definition 
Die Widerstände sind Elemente in Form von Zylindern und haben Ringe, die ihre Werte angeben:
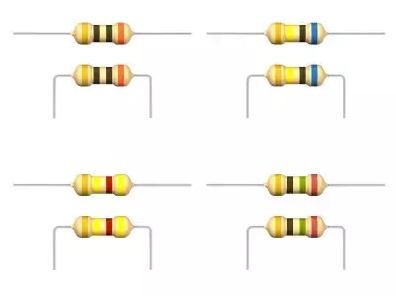
ID:(11762, 0)
Widerstandssymbole
Notiz 
Abhängig von der Herkunft der Diagramme gibt es zwei Symbole. Amerikaner zeichnen die Widerstände als Zickzacklinien, während in Europa ein Rechteck verwendet wird:
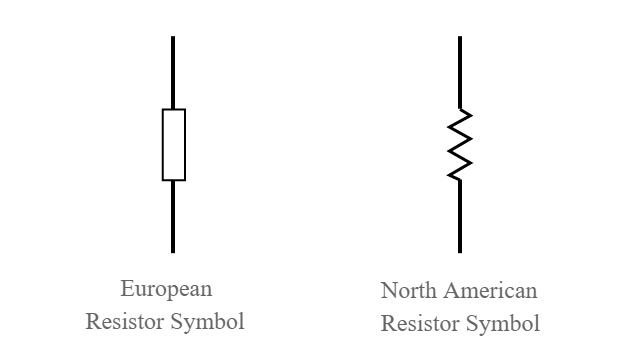
ID:(11764, 0)
Schaltplan
Zitat 
Este es un circuito para una sirena. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con números)
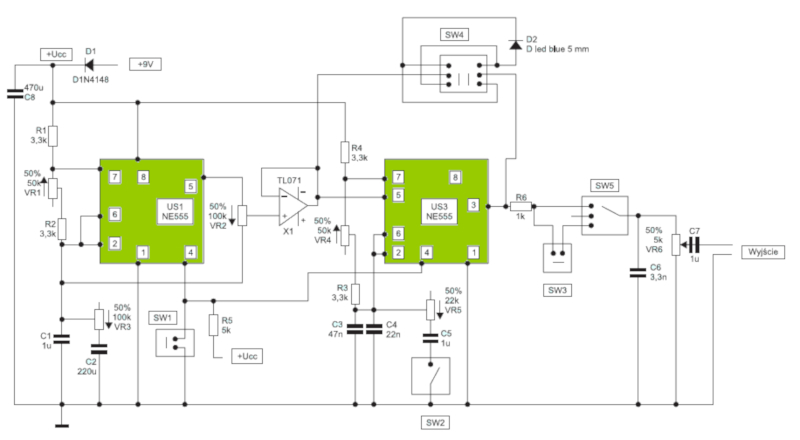
ID:(11704, 0)
Beispiel einer gedruckten Schaltung
Übung 
Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con métodos fotoquimicos. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• procesadores (cajas rectangulares con números)

ID:(11705, 0)
Widerstand
Beschreibung 
Widerstände sind Elemente, die die Erzeugung definierter Ströme ermöglichen und direkte Entladungen vermeiden.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
Die Widerst nde sind Elemente in Form von Zylindern und haben Ringe, die ihre Werte angeben:

(ID 11762)
Der Wert ist mit farbigen Ringen codiert:
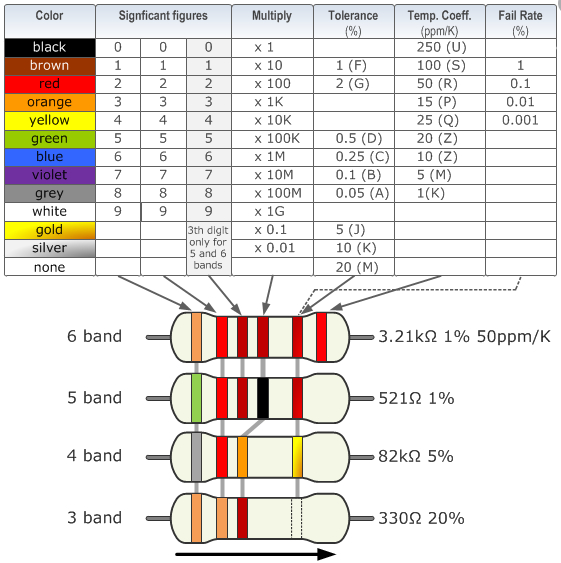
(ID 11763)
Abh ngig von der Herkunft der Diagramme gibt es zwei Symbole. Amerikaner zeichnen die Widerst nde als Zickzacklinien, w hrend in Europa ein Rechteck verwendet wird:

(ID 11764)
Este es un circuito para una sirena. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con n meros)

(ID 11704)
Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con m todos fotoquimicos. En el se reconocen en particular
• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rect ngulo alargado)
• procesadores (cajas rectangulares con n meros)

(ID 11705)
Das Diagramm, das in Reihe geschaltete Widerst nde darstellt, hat die folgende Form:

(ID 7862)
Al conectarse resistencias
$\Delta\varphi=\displaystyle\sum_i \Delta\varphi_i$
Como la corriente
$\Delta\varphi_i=R_i I$
Si se reemplaza esta expresi n en la suma de las diferencias de potencial se obtiene
$\Delta\varphi=\displaystyle\sum_i R_iI$
por lo que la resistencia en serie se calcula como la suma de las resistencias individuales con :
| $ R_s =\displaystyle\sum_ i R_i $ |
(ID 3215)
Das Diagramm, das parallel geschaltete Widerst nde darstellt, hat die folgende Form:
xa0

(ID 7861)
Al conectarse resistencias
$I=\displaystyle\sum_iI_i$
Como en cada resistencia se cumple la ley de Ohm
$\Delta\varphi=R_iI_i$
la suma de corrientes se puede escribir como
$I=\displaystyle\sum_i\displaystyle\frac{\Delta\varphi}{R_i}$
Por ello se puede definir una resistencia total para el caso de suma paralela es con de la forma
| $\displaystyle\frac{1}{ R_p }=\displaystyle\sum_i\displaystyle\frac{1}{ R_i }$ |
(ID 225)
ID:(1585, 0)
