Storyboard

Las resistencias son elementos que permiten generar corrientes definidas evitando las descargas directas.

>Modelo

ID:(1585, 0)

Imagen

>Top

Las resistencias son elementos con la forma de cilindros y tienen anillos que indican sus valores:

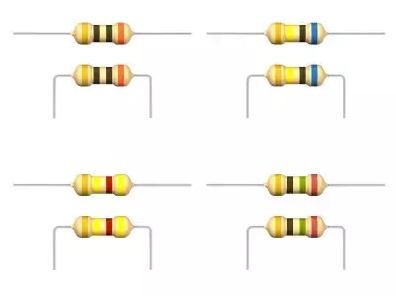
ID:(11762, 0)

Imagen

>Top

El valor se codifica con anillos de colores:

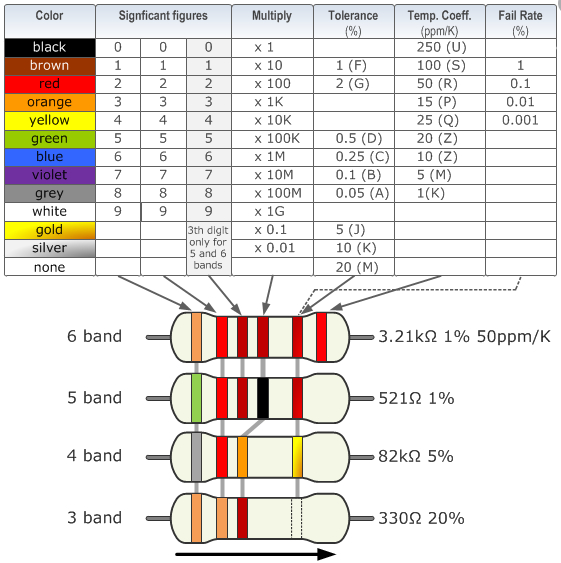
ID:(11763, 0)

Imagen

>Top

Existen dos símbolos según el origen de los diagramas. Americanos dibujan las resistencias como lineas en zig-zag mientras que en Europa se emplea un rectángulo:

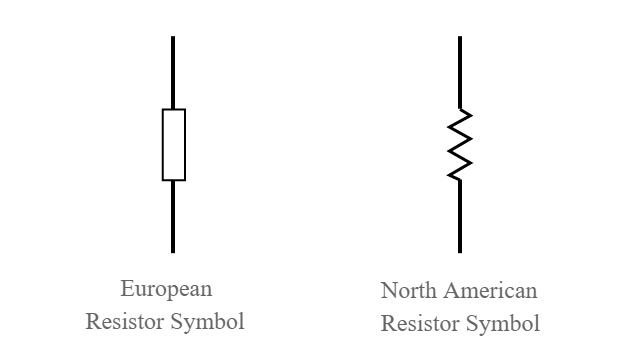
ID:(11764, 0)

Imagen

>Top

Este es un circuito para una sirena. En el se reconocen en particular

• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• transistores (un triangulo con tres conectores)
• procesadores (cajas rectangulares con números)

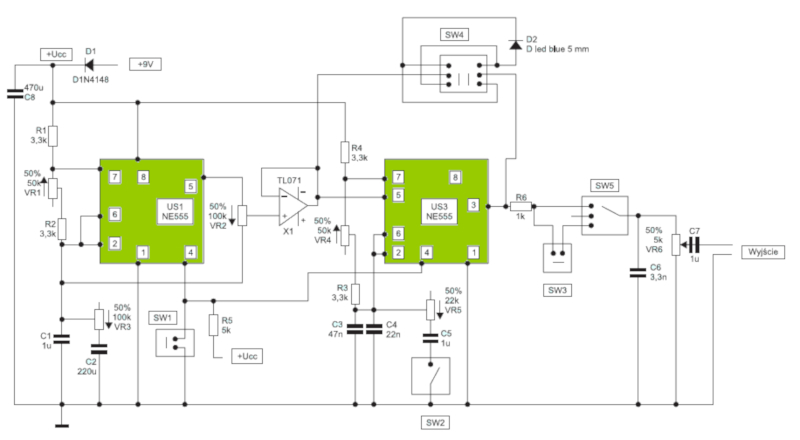
ID:(11704, 0)

Imagen

>Top

Este es un circuito impreso, es decir se generaron las conexiones entre los elementos con métodos fotoquimicos. En el se reconocen en particular

• capacitores (dos rayas paralelas de mismo largo)
• resistencias (un rectángulo alargado)
• procesadores (cajas rectangulares con números)

ID:(11705, 0)

Imagen

>Top

El diagrama que representa resistencias conectadas en serie tiene la siguiente forma:

ID:(7862, 0)

Ecuación

>Top, >Modelo

Al conectarse resistencias R_i en serie en cada una ocurrirá una caída de potencial \Delta\varphi_i cuya suma será igual a la diferencia de potencial total

$\Delta\varphi=\displaystyle\sum_i \Delta\varphi_i$

Como la corriente I es igual en todas las resistencias la ley de Ohm en la i-esima resistencia será

$\Delta\varphi_i=R_i I$

Si se reemplaza esta expresión en la suma de las diferencias de potencial se obtiene

$\Delta\varphi=\displaystyle\sum_i R_iI$

por lo que la resistencia en serie se calcula como la suma de las resistencias individuales con :

$ R_s =\displaystyle\sum_ i R_i $

Condiciones

Variables

$R_s$

Resistencia en Serie

$Ohm$

5498

$R_i$

Resistencia i

$Ohm$

8816

Relación

ID:(3215, 0)

Imagen

>Top

El diagrama que representa resistencias conectadas en paralelo tiene la siguiente forma:

ID:(7861, 0)

Ecuación

>Top, >Modelo

Al conectarse resistencias R_i en paralelo la diferencia de potencial es para todas iguales pero la corrientes son dependen de la resistencia respectiva y tomarán un valor I_i. La suma de las corrientes individuales será igual a la corriente total I:

$I=\displaystyle\sum_iI_i$

Como en cada resistencia se cumple la ley de Ohm

$\Delta\varphi=R_iI_i$

la suma de corrientes se puede escribir como

$I=\displaystyle\sum_i\displaystyle\frac{\Delta\varphi}{R_i}$

Por ello se puede definir una resistencia total para el caso de suma paralela es con de la forma

$\displaystyle\frac{1}{ R_p }=\displaystyle\sum_i\displaystyle\frac{1}{ R_i }$

Condiciones

Variables

$R_p$

Resistencia en Paralelo

$Ohm$

5499

$R_i$

Resistencia i

$Ohm$

8816

Relación

ID:(225, 0)