Utilisateur:
Position
Storyboard 
Pour définir la position d'un objet, un système de coordonnées est introduit, ce qui permet d'établir un point d'origine et de définir la position en mesurant la distance le long d'une ligne droite ou d'une courbe. Par conséquent, l'unité de position correspond à une mesure de longueur, telle que les kilomètres, les mètres, les centimètres, et ainsi de suite.
Le choix du système de coordonnées est flexible et est fait pour simplifier autant que possible la modélisation et les calculs associés. Par exemple, si l'objet se déplace le long d'une piste, qui n'est pas nécessairement droite, il est avantageux de définir le système de coordonnées le long de cette piste. Dans ce cas spécifique, la position est définie comme la distance depuis l'origine ou le point de départ de la piste.
ID:(607, 0)
Mécanismes
Iframe
Une des variables clés pour décrire le mouvement d'un corps est sa position. Cela peut être soit un scalaire, définissant la distance par rapport à un point de référence dans le cas d'une situation unidimensionnelle, soit un vecteur avec un origine dans le cas de plusieurs dimensions.
Mécanismes
ID:(15380, 0)
Référence de mesure de longueur
Concept
Chaque mesure correspond à une comparaison d'une valeur spécifique avec un modèle de référence, ce qui donne la valeur dans l'unité correspondante.
Au fil du temps, ces modèles ont évolué, atteignant une précision accrue. Les exemples incluent :
Fausse copie du premier étalon de mètre (notez l'orthographe incorrecte), scellée dans les fondations d'un immeuble, 36 rue de Vaugirard, Paris, Ken Eckert (Wikimedia Commons)
Une copie du mètre provisoire installé de 1796 à 1797, située sur le mur d'un bâtiment au 36 rue de Vaugirard, à Paris
Répliques historiques néerlandaises d'étalons métriques dans la collection du Rijksmuseum d'Amsterdam : mètre en fer avec étui (construit par Étienne Lenoir, 1799; numéro de catalogue NG-2001-16-C-8), kilogramme funéraire en cuivre avec étui (1798; numéro de catalogue NG-2001-16-D-9), mesures de volume en cuivre ( 1829 ; numéro de catalogue NG-2001-16-B-28)., Yerpo (Wikimedia Commons)
En 1799, Étienne Lenoir a fabriqué les normes de platine et douze de fer du mètre.
Rule (Modifié à partir de Wikimedia Commons, Une règle, représentant deux unités habituelles de longueur, le centimètre et le pouce)
La règle graduée comprend une échelle graduée longitudinale en acier inoxydable pour éviter que la formation de rouille n'entrave la lecture ou n'efface l'échelle.
ID:(2238, 0)
Méthode de mesure de la longueur
Concept
Il existe de nombreuses méthodes pour mesurer des distances, notamment:
1. Règle ou mètre ruban : c'est une méthode simple et commune pour mesurer de petites distances. Il s'agit de placer la règle ou le mètre ruban directement contre l\'objet à mesurer et de lire la longueur.
2. Odomètre : un odomètre est un dispositif qui mesure la distance parcourue par un véhicule ou un autre objet en mouvement. Il fonctionne en comptant le nombre de révolutions d\'une roue ou d\'une autre pièce en mouvement.
3. Télémètre laser : un télémètre laser utilise un faisceau laser pour déterminer la distance entre le dispositif et la cible. Il mesure le temps qu\'il faut au faisceau laser pour rebondir sur la cible et revenir au dispositif.
4. GPS (Système de Positionnement Global) : le GPS est un système basé sur des satellites qui peut être utilisé pour déterminer l\'emplacement et la distance entre deux points sur la surface de la Terre. Il fonctionne en triangulant la position d\'un récepteur GPS à partir de signaux de plusieurs satellites GPS.
Ce sont là quelques exemples de méthodes pour mesurer des distances, et il existe de nombreuses autres techniques et dispositifs qui peuvent être utilisés en fonction de l\'application spécifique et du niveau de précision requis.
ID:(472, 0)
Règle ou ruban à mesurer
Description
Une règle ou un mètre ruban sont tous deux des méthodes de mesure de la longueur. Une règle est un dispositif de mesure plat marqué avec des unités de longueur telles que des pouces, des centimètres ou des millimètres. Un mètre ruban est un dispositif de mesure souple marqué avec des unités de longueur. Les mètres rubans sont généralement plus précis que les règles, car ils peuvent mesurer des surfaces courbes et peuvent être étendus à des longueurs plus grandes.
ID:(12508, 0)
Odomètre
Description
Un odomètre est un appareil utilisé pour mesurer la distance parcourue par un véhicule. Il est généralement situé sur le tableau de bord ou le tableau de bord d'une voiture et peut être utilisé pour suivre la distance totale parcourue. Un odomètre fonctionne en comptant le nombre de tours d'un arbre de transmission relié aux roues du véhicule. Lorsque le véhicule se déplace, l'arbre de transmission tourne et chaque tour de l\'arbre de transmission est compté et enregistré sur l\'odomètre. L\'odomètre est généralement étalonné pour qu\'il puisse mesurer avec précision les distances parcourues en miles ou en kilomètres.
ID:(480, 0)
Télémètre laser
Description
Un télémètre laser est un dispositif qui utilise un faisceau laser pour mesurer la distance entre deux points. Il fonctionne en envoyant un pulse laser, qui est réfléchi par l'objet mesuré et ensuite détecté par le télémètre laser. Le temps qu'il faut au pulse laser pour aller du télémètre laser à l'objet et retour peut alors être utilisé pour calculer la distance entre les deux points. Les télémètres laser sont couramment utilisés dans le cadre de levés topographiques, de navigation et d'autres applications où des mesures précises sont nécessaires.
ID:(481, 0)
GPS (Système de positionnement global)
Description
Le système de positionnement global (GPS) est un système de navigation par satellite qui utilise un réseau de 24 satellites orbitant autour de la Terre pour déterminer l'emplacement exact d'une personne ou d'un objet sur la planète. Les récepteurs GPS calculent la distance à chaque satellite en mesurant le temps qu\'il faut aux signaux pour voyager du satellite au récepteur. Une fois ces distances connues, le récepteur peut utiliser un processus appelé trilatération pour calculer sa position exacte, y compris la longitude et la latitude, ainsi que l\'altitude. Cela peut être utilisé pour mesurer les distances entre deux emplacements, ainsi que la longueur d\'un chemin parcouru par une personne ou un objet.
ID:(474, 0)
Position dans plus de dimensions
Concept
La position ou l'emplacement d'un objet dans un système à plus d\'une dimension est traditionnellement défini en utilisant un vecteur. Ce vecteur part de l\'origine du système de coordonnées jusqu\'à l\'objet, avec le même nombre de composantes qu\'il y a de dimensions.
ID:(477, 0)
Représentation de la position dans une dimension
Concept
Dans un système à une dimension, la position d'un objet peut être représentée par un scalaire, qui indique la distance de l'origine de zéro dans la direction dans laquelle se trouve l'objet. Cette distance est mesurée comme une quantité positive ou négative, selon que l\'objet est dans la direction positive ou négative de l\'axe. Cette position peut être représentée, par exemple, par le paramètre $x$ ou $s$, où les scalaires $x$ ou $s$ indiquent la distance de l\'origine à la position de l\'objet.
ID:(2251, 0)
Représentation de la position en deux dimensions
Concept
Dans un système à deux dimensions, la position d'un objet peut être représentée par un vecteur, qui indique la distance à partir de l'origine de zéro (coordonnées $(0,0)$) dans la direction où se trouve l'objet. Les deux coordonnées sont mesurées en tant que quantité positive ou négative, selon que l\'objet se trouve dans la direction positive ou négative de l\'axe correspondant. Cette position peut être représentée, par exemple, par le paramètre $(x, y)$, où les scalaires $x$ et $y$ indiquent la distance à partir de l\'origine de l\'objet sur chaque axe.
ID:(2234, 0)
Représentation de la position en trois dimensions
Concept
Dans un système à deux dimensions, la position d'un objet peut être représentée par un vecteur, qui indique la distance à partir de l'origine de zéro (coordonnées $(0,0,0)$) dans la direction où se trouve l'objet. Les deux coordonnées sont mesurées en tant que quantité positive ou négative, selon que l\'objet se trouve dans la direction positive ou négative de l\'axe correspondant. Cette position peut être représentée, par exemple, par le paramètre $(x, y, z)$, où les scalaires $x$, $y$ et $z$ indiquent la distance à partir de l\'origine de l\'objet sur chaque axe.
ID:(2235, 0)
Position
Concept
A position ($s$) d'un objet dans un système unidimensionnel fait référence à l'emplacement de l\'objet par rapport à un point de référence. Cette position est exprimée comme la distance entre l\'objet et le point d\'origine. Cette distance peut être une ligne droite sur un axe cartésien, ou elle peut suivre un chemin courbe.
ID:(15, 0)
Position initiale
Concept
A vitesse ($s_0$) est l'emplacement de départ d'un objet avant que tout mouvement ne commence. Cette position est définie comme la distance entre l\'objet et le point d\'origine. Cette distance peut être une ligne droite sur un axe cartésien ou elle peut suivre une trajectoire courbe.
ID:(10302, 0)
Distance parcourue
Concept
A distance parcourue en un temps ($\Delta s$) par un objet est mesurée en mesurant la distance entre deux points spécifiques le long d'une trajectoire. Cette trajectoire peut être une ligne droite sur un axe cartésien ou un chemin courbe. La distance est calculée en mesurant la longueur de la trajectoire entre les deux points de départ et d'arrivée.
ID:(9495, 0)
Distance infinitésimale
Concept
A distance infinitésimale parcourue ($ds$) entre deux points est une mesure de distance si petite que le mouvement entre les deux points peut être considéré comme uniforme.
Généralement, les différences d'une variable sont notées en ajoutant le symbole $\Delta$ avant la lettre correspondante, de sorte que la variation de la position $s$ est représentée comme $\Delta s$. Pour les variations infinitésimales, on utilise un $d$ à la place de $\Delta$, ainsi une variation infinitésimale de la position serait représentée comme $ds$.
ID:(14451, 0)
Mesure de la distance parcourue
Top
Pour décrire le mouvement d'un objet, nous devons calculer a distance parcourue en un temps ($\Delta s$). Cette distance est obtenue en mesurant a vitesse ($s_0$) et a position ($s$) de cet objet. Si les mouvements sont unidimensionnels, la distance parcourue est déterminée en soustrayant la position initiale de la position finale.
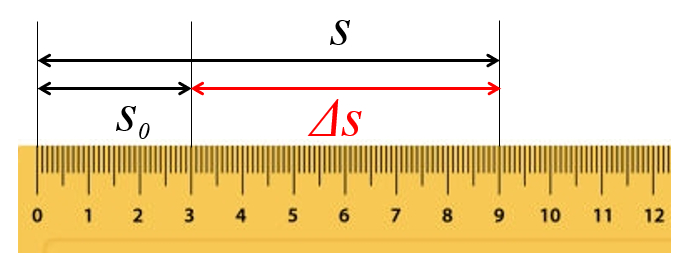
ID:(15382, 0)
Distance parcourue dans plusieurs dimensions
Concept
Pour décrire le mouvement d'un objet, nous calculons la différence entre un point de départ et un point d'arrivée. Cette différence, appelée distance, ne correspond pas toujours à la distance réelle parcourue par l\'objet si le chemin est courbe. La courbure du chemin fait que la distance parcourue est supérieure à la distance entre les deux points. Si les deux points sont très proches, la courbure est négligeable et la distance parcourue correspond à la distance entre les deux points.
Dans ce cas, on parle d\'une distance infinitésimale.
ID:(9496, 0)
Distance infinitésimale dans plus de dimensions
Concept
Pour modéliser le mouvement d'un corps, il est nécessaire de décrire comment il se déplace, c'est-à-dire le chemin et la direction dans lesquels il se déplace. Si le chemin est courbé, le vecteur entre la position actuelle et future ne correspondra pas nécessairement au chemin réel, sauf si le chemin est infinitésimal. Dans ce cas, la déviation du segment est négligeable et l\'arc correspond au vecteur tangentiel de la courbe.
ID:(14452, 0)
Modèle
Top
En ce qui concerne la position (dans le cas des scalaires comme a position ($s$) et comme vecteur a position réelle ($\vec{s}$)), nous pouvons définir le chemin parcouru. Celui-ci peut être macroscopique (dans le cas des scalaires comme a distance parcourue en un temps ($\Delta s$) et comme vecteur a distance parcourue ($\Delta\vec{s}$)), ce qui peut ne pas refléter que le chemin peut ne pas être rectiligne. Si nous voulons étudier le chemin réel, nous devons considérer des variations infinitésimales (dans le cas des scalaires comme a distance infinitésimale parcourue ($ds$) et comme vecteur le élément de chemin parcouru ($d\vec{s}$)), dans lesquelles, dans une première approximation, on peut considérer qu'il est rectiligne.
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $
&Ds = &s - &s_0
$ \Delta s \equiv s - s_0 $
Ds = s - s_0
$d\vec{s} \equiv \vec{s} - \vec{s}_0 $
d&s = &s - &s_0
$ds \equiv s - s_0 $
ds = s - s_0
ID:(15381, 0)
Distance parcourue
Équation
Nous pouvons calculer a distance parcourue en un temps ($\Delta s$) à partir de a vitesse ($s_0$) et a position ($s$) grâce à l'équation suivante :
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Distance infinitésimale
Équation
Si l'on souhaite étudier le mouvement d'un corps se déplaçant de manière non uniforme, il est nécessaire de travailler à une échelle plus petite où les fluctuations ne sont pas significatives. Pour cela, on introduit le concept de déplacement infinitésimal, qui est calculé en soustrayant la position actuelle de la position précédente, qui doit être très proche de la première.
Par conséquent, a distance infinitésimale parcourue ($ds$) est introduit comme la différence entre a position ($s$) et a vitesse ($s_0$) comme suit :
| $ds \equiv s - s_0 $ |
ID:(14450, 0)
Distance parcourue dans plusieurs dimensions
Équation
Pour décrire le mouvement d'un objet, il est nécessaire de calculer la distance qu'il a parcourue. Pour ce faire, les points initial et final de l'objet sont définis à l'aide de vecteurs, et la distance est calculée en soustrayant un vecteur de l'autre. Cela ne correspond au trajet parcouru que si le déplacement est rectiligne, ce qui est généralement vrai lorsque les deux points sont très proches, comme dans le cas de a distance parcourue ($\Delta\vec{s}$) en soustrayant a position d'origine ($\vec{s}_0$) de a position réelle ($\vec{s}$) :
| $ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
ID:(714, 0)
Distance infinitésimale dans plus de dimensions
Équation
Dans le cas d'un espace avec plus d\'une dimension, le chemin entre deux points ne doit pas nécessairement être rectiligne, comme c\'est le cas dans les espaces à une dimension. Dans ce type de situation, un vecteur qui représente la distance entre deux points le long du chemin sera toujours égal ou inférieur à la distance réelle le long du chemin. Cependant, ils coïncideront si la distance entre les deux points est infiniment petite ou très petite. Par conséquent, il est utile de définir le vecteur infinitésimal, qui permet de décrire le comportement d\'un objet dans un espace continu de manière précise.
Par conséquent, le élément de chemin parcouru ($d\vec{s}$) est introduit comme la différence entre a position réelle ($\vec{s}$) et a position d'origine ($\vec{s}_0$) comme suit :
| $d\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
ID:(9497, 0)