User:
Position
Storyboard 
To define the position of an object, a coordinate system is introduced that allows establishing an origin point and defining the position by measuring the distance along a straight line or a curve. As a result, the unit of position corresponds to a length measurement, such as kilometers, meters, centimeters, and so on.
The choice of the coordinate system is flexible and is made to simplify the modeling and associated calculations as much as possible. For instance, if the object moves along a track, which may not necessarily be straight, it is advantageous to define the coordinate system along that track. In this specific case, the position is defined as the distance from the origin or the starting point of the track.
ID:(607, 0)
Mechanisms
Iframe
One of the key variables for describing the motion of a body is its position. This can either be a scalar, defining the distance to a reference point in the case of a one-dimensional situation, or a vector with an origin in the case of more than one dimension.
Mechanisms
ID:(15380, 0)
Length measurement reference
Concept
Each measurement corresponds to a comparison of a specific value and a reference pattern, resulting in the value being obtained in the corresponding unit.
Over time, these patterns have evolved, achieving greater accuracy. Examples include:
Fake copy of the first metre standard (notice the incorrect spelling), sealed in the foundation of a building, 36 rue de Vaugirard, Paris, Ken Eckert (Wikimedia Commons)
A copy of the provisional meter installed from 1796 to 1797, located on the wall of a building at 36 rue de Vaugirard, Paris
Historic Dutch replicas of metric standards in the collection of Rijksmuseum, Amsterdam: iron metre with case (constructed by Étienne Lenoir, 1799; catalog number NG-2001-16-C-8), copper grave kilogram with case (1798; catalog number NG-2001-16-D-9), copper volume measures (1829; catalog number NG-2001-16-B-28)., Yerpo (Wikimedia Commons)
In 1799, Étienne Lenoir fabricated the platinum and twelve iron standards of the meter.
Rule (Modified from Wikimedia Commons, A ruler, depicting two customary units of length, the centimetre and the inch)
The graduated ruler includes a longitudinal graduated scale made of stainless steel to prevent rust formation from hindering reading or erasing the scale.
ID:(2238, 0)
Length measurement method
Concept
There are many methods for measuring distances, including:
1. Ruler or Tape Measure: This is a simple and common method for measuring small distances. It involves placing the ruler or tape measure directly against the object being measured and reading the length.
2. Odometer: An odometer is a device that measures the distance traveled by a vehicle or other moving object. It works by counting the number of revolutions of a wheel or other moving part.
3. Laser Rangefinder: A laser rangefinder uses a laser beam to determine the distance between the device and the target. It measures the time it takes for the laser beam to bounce off the target and return to the device.
4. GPS (Global Positioning System): GPS is a satellite-based system that can be used to determine the location and distance between two points on the Earth's surface. It works by triangulating the position of a GPS receiver based on signals from several GPS satellites.
These are just a few examples of methods for measuring distances, and there are many other techniques and devices that can be used depending on the specific application and level of precision required.
ID:(472, 0)
Ruler or Tape Measure
Description
Ruler or Tape Measure are both methods of measuring length. A ruler is a flat measuring device that is marked with units of length such as inches, centimeters or millimeters. A tape measure is a flexible measuring device that is marked with units of length. Tape measures are usually more accurate than rulers, as they can measure curved surfaces and can be extended to greater lengths.
ID:(12508, 0)
Odometer
Description
An odometer is a device used to measure the distance traveled by a vehicle. It is typically located on the dashboard or instrument panel of a car and can be used to track the total distance traveled. An odometer works by counting the number of revolutions of a drive shaft connected to the wheels of the vehicle. As the vehicle moves, the drive shaft turns, and each revolution of the drive shaft is counted and recorded on the odometer. The odometer is typically calibrated so that it can accurately measure distances traveled in miles or kilometers.
ID:(480, 0)
Laser rangefinder
Description
A laser rangefinder is a device that uses a laser beam to measure the distance between two points. It works by sending out a laser pulse, which is reflected off of the object being measured and then detected by the rangefinder. The time it takes for the laser pulse to travel from the rangefinder to the object and back can then be used to calculate the distance between the two points. Laser rangefinders are commonly used in surveying, navigation, and other applications where precise measurements are needed.
ID:(481, 0)
GPS (Global Positioning System)
Description
The Global Positioning System (GPS) is a satellite-based navigation system that uses a network of 24 satellites orbiting the Earth to determine the exact location of a person or object on the planet. GPS receivers calculate the distance to each satellite by measuring the amount of time it takes for signals to travel from the satellite to the receiver. Once these distances are known, the receiver can use a process called trilateration to calculate its exact location, including longitude and latitude, as well as altitude. This can be used to measure distances between two locations, as well as the length of a path taken by a person or object.
ID:(474, 0)
Position in more dimensions
Concept
The position or location of an object in a system with more than one dimension is traditionally defined using a vector. This vector goes from the origin of the coordinate system to the object, with the same number of components as there are dimensions.
ID:(477, 0)
Representation of position in one dimension
Concept
In a one-dimensional system, the position of an object can be represented by a scalar, which indicates the distance from the origin of zero in the direction in which the object is located. This distance is measured as a positive or negative quantity, depending on whether the object is in the positive or negative direction of the axis. This position can be represented, for example, by the parameter $x$ or $s$, where the scalars $x$ or $s$ indicate the distance from the origin to the position of the object.
One-dimensional vector to describe a position
ID:(2251, 0)
Representation of the position in two dimensions
Concept
In a two-dimensional system, the position of an object can be represented by a vector, which indicates the distance from the origin of zero (coordinates $(0,0)$) in the direction in which the object is located. Both coordinates are measured as a positive or negative amount, depending on whether the object is in the positive or negative direction of the respective axis. This position can be represented, for example, with the parameter $(x,y)$, where the scalars $x$ and $y$ indicate the distance from the origin of the object in each axis.
ID:(2234, 0)
Representation of the position in three dimensions
Concept
In a two-dimensional system, the position of an object can be represented by a vector, which indicates the distance from the origin of zero (coordinates $(0,0,0)$) in the direction in which the object is located. Both coordinates are measured as a positive or negative amount, depending on whether the object is in the positive or negative direction of the respective axis. This position can be represented, for example, with the parameter $(x,y,z)$, where the scalars $x$, $y$ and $z$ indicate the distance from the origin of the object in each axis.
ID:(2235, 0)
Position
Concept
The position ($s$) of an object in a one-dimensional system refers to the location of the object in relation to a reference point. This location is expressed as the distance between the object and the origin point. This distance can be a straight line on a Cartesian axis, or it can follow a curved path:
ID:(15, 0)
Initial position
Concept
The starting position ($s_0$) is the starting location of an object before any motion begins. This location is defined as the distance between the object and the origin point. This distance can be a straight line on a Cartesian axis or it can follow a curved path.
ID:(10302, 0)
Distance traveled
Concept
The distance traveled in a time ($\Delta s$) by an object is measured by measuring the distance between two specific points along a trajectory. This trajectory can be a straight line on a Cartesian axis or a curved path. The distance is calculated by measuring the length of the trajectory between the two starting and ending points.
ID:(9495, 0)
Infinitesimal distance
Concept
The infinitesimal distance traveled ($ds$) between two points is a measurement so small that the motion between them can be considered uniform, or in other words, at constant velocity.
Generally, differences of a variable are denoted by adding the symbol $\Delta$ before the corresponding letter, so the variation in position $s$ is represented as $\Delta s$. For infinitesimal variations, a $d$ is used instead of $\Delta$, thus an infinitesimal variation in position would be represented as $ds$.
ID:(14451, 0)
Measurement of distance traveled
Top
To describe the movement of an object, we need to calculate the distance traveled in a time ($\Delta s$). This distance is obtained by measuring the starting position ($s_0$) and the position ($s$) from the object. If the movements are one-dimensional, the distance traveled is determined by subtracting the initial position from the final position.
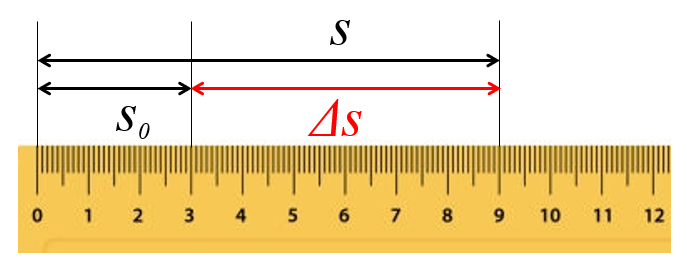
ID:(15382, 0)
Distance traveled in more dimensions
Concept
To describe the motion of an object, it is necessary to consider the distance between its starting point and its ending point. However, this distance does not always reflect the actual distance traveled by the object, as a curved path will make the distance traveled greater than the distance between the starting and ending points. If the two points are very close together, the curvature will be negligible and therefore the distance traveled will coincide with the distance between the two points.
In this case we speak of an infinitesimal distance.
ID:(9496, 0)
Infinitesimal distance in more dimensions
Concept
To model the motion of a body, it is necessary to describe how it moves, that is, the path and the direction in which it moves. If the path is curved, the vector between the current and future position may not necessarily coincide with the actual path, unless the path is infinitesimal. In such a case, the deviation from the segment is negligible, and the arc corresponds to the tangential vector of the curve.
ID:(14452, 0)
Model
Top
Regarding position (in the case of scalars like the position ($s$) and as a vector like the current Position ($\vec{s}$)), the traveled path can be defined. This path can be macroscopic (in the case of scalars like the distance traveled in a time ($\Delta s$) and as a vector like the distance Run ($\Delta\vec{s}$)), which may not reflect that the path may not be rectilinear. If we are interested in studying the actual path, we must consider infinitesimal variations (in the case of scalars like the infinitesimal distance traveled ($ds$) and as a vector like the path element traveled ($d\vec{s}$)), in which, in a first approximation, it can be considered rectilinear.
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $
&Ds = &s - &s_0
$ \Delta s \equiv s - s_0 $
Ds = s - s_0
$d\vec{s} \equiv \vec{s} - \vec{s}_0 $
d&s = &s - &s_0
$ds \equiv s - s_0 $
ds = s - s_0
ID:(15381, 0)
Distance traveled
Equation
We can calculate the distance traveled in a time ($\Delta s$) from the starting position ($s_0$) and the position ($s$) using the following equation:
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Infinitesimal distance
Equation
If one wishes to study the motion of a body that moves non-uniformly, it is necessary to work on a smaller scale where fluctuations are not relevant. To achieve this, the concept of infinitesimal displacement is introduced, which is calculated by subtracting the current position from the previous position, which must be very close to the first.
Therefore, the infinitesimal distance traveled ($ds$) is introduced as the difference between the position ($s$) and the starting position ($s_0$) as:
| $ds \equiv s - s_0 $ |
ID:(14450, 0)
Distance traveled in more dimensions
Equation
To describe the motion of an object, it is necessary to calculate the distance it has traveled. To do this, the initial and final points of the object are defined using vectors, and the distance is calculated by subtracting one vector from the other. This only coincides with the path traveled if the displacement is rectilinear, which is generally true when both points are very close, as in the case of the distance Run ($\Delta\vec{s}$) subtracting the position of Origin ($\vec{s}_0$) from the current Position ($\vec{s}$):
| $ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
ID:(714, 0)
Infinitesimal distance in more dimensions
Equation
In the case of a space with more than one dimension, the path between two points does not necessarily have to be straight, as is the case in one-dimensional spaces. In these types of situations, a vector representing the distance between two points along the path will always be equal to or smaller than the actual distance along the path. However, they will coincide if the distance between the two points is infinitesimal or very small. Therefore, it is useful to define the infinitesimal vector, which allows us to describe the behavior of an object in a continuous space precisely.
Therefore, the path element traveled ($d\vec{s}$) is introduced as the difference between the current Position ($\vec{s}$) and the position of Origin ($\vec{s}_0$) as:
| $d\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
ID:(9497, 0)