Usuario:
Posición
Storyboard 
Para determinar la posición de un objeto, se introduce un sistema de coordenadas que permite establecer un punto de origen y definir la posición mediante la medición de la distancia a lo largo de una línea recta o una curva. Por tanto, la unidad de posición corresponde a una longitud, como kilómetros, metros, centímetros, y así sucesivamente.
La elección del sistema de coordenadas es flexible y se busca con el propósito de simplificar al máximo la modelación y los cálculos asociados. Por ejemplo, si el objeto se desplaza a lo largo de una vía, que no necesariamente es recta, es conveniente definir el sistema de coordenadas a lo largo de esa vía. En este caso particular, la posición se define como la distancia desde el origen o el punto de inicio de la vía.
ID:(607, 0)
Mecanismos
Iframe
Una de las variables clave para describir el movimiento de un cuerpo es su posición. Esta puede ser tanto un escalar, que define la distancia a un punto de referencia en el caso de una situación unidimensional, como un vector con un origen en el caso de más de una dimensión.
Mecanismos
ID:(15380, 0)
Referencia de medición de largos
Concepto
Cada medición corresponde a una comparación de valor determinado y un patrón de referencia con lo que se obtiene el valor en la unidad correspondiente.
Los patrones han ido cambiando en el tiempo logrando cada vez una mayor exactitud. Ejemplos son:
Copia falsa del primer estándar metro (nótese la ortografía incorrecta), sellada en los cimientos de un edificio, 36 rue de Vaugirard, París, Ken Eckert (Wikimedia Commons)
Una copia del metro provisional instalado de 1796 a 1797, ubicado en la pared de un edificio, 36 rue de Vaugirard, París
Réplicas históricas holandesas de estándares métricos en la colección del Rijksmuseum, Amsterdam: medidor de hierro con caja (construido por Étienne Lenoir, 1799; número de catálogo NG-2001-16-C-8), kilogramo de tumba de cobre con caja (1798; número de catálogo NG-2001-16-D-9), medidas de volumen de cobre ( 1829; número de catálogo NG-2001-16-B-28)., Yerpo (Wikimedia Commons)
En 1799, Étienne Lenoir fabricó los estándares de platino y doce de hierro del metro.
Rule (Modificado de Wikimedia Commons, una regla que representa dos unidades habituales de longitud, el centímetro y la pulgada)
La regla graduada incluye una escala graduada longitudinal fabricadas en acero inoxidable para evitar que la formación de óxido dificulte la lectura o borre la escala.
ID:(2238, 0)
Método de medición de largos
Concepto
En español: Existen muchos métodos para medir distancias, entre ellos:
1. Regla o cinta métrica: Esta es una forma simple y común de medir distancias cortas. Consiste en colocar la regla o la cinta métrica directamente en el objeto que se está midiendo y leer la longitud.
2. Odómetro: Un odómetro es un dispositivo que mide la distancia recorrida por un vehículo u otro objeto en movimiento. Funciona contando el número de revoluciones de una rueda u otra parte en movimiento.
3. Telémetro láser: Un telémetro láser utiliza un rayo láser para determinar la distancia entre el dispositivo y el objetivo. Mide el tiempo que tarda el rayo láser en rebotar en el objetivo y volver al dispositivo.
4. GPS (Sistema de Posicionamiento Global): El GPS es un sistema basado en satélites que se puede usar para determinar la ubicación y la distancia entre dos puntos en la superficie de la Tierra. Funciona triangulando la posición de un receptor GPS basado en señales de varios satélites GPS.
Estos son solo algunos ejemplos de métodos para medir distancias, y hay muchas otras técnicas y dispositivos que se pueden usar según la aplicación específica y el nivel de precisión requerido.
ID:(472, 0)
Regla o cinta métrica
Descripción
Una regla o una cinta métrica son ambos métodos para medir la longitud. Una regla es un dispositivo de medición plano marcado con unidades de longitud como pulgadas, centímetros o milímetros. Una cinta métrica es un dispositivo de medición flexible marcado con unidades de longitud. Las cintas métricas suelen ser más precisas que las reglas, ya que pueden medir superficies curvas y se pueden extender a mayores longitudes.
ID:(12508, 0)
Odómetro
Descripción
Un odómetro es un dispositivo utilizado para medir la distancia recorrida por un vehículo. Normalmente se encuentra en el tablero o panel de instrumentos de un auto y se puede usar para registrar la distancia total recorrida. Un odómetro funciona contando el número de revoluciones de un eje de transmisión conectado a las ruedas del vehículo. A medida que el vehículo avanza, el eje de transmisión gira y cada revolución del eje de transmisión se contabiliza y registra en el odómetro. El odómetro suele estar calibrado de modo que pueda medir con precisión distancias recorridas en millas o kilómetros.
ID:(480, 0)
Localizador Laser
Descripción
Un láser de medición es un dispositivo que utiliza un rayo láser para medir la distancia entre dos puntos. Funciona enviando un pulso láser, que es reflejado por el objeto que se está midiendo y luego detectado por el láser de medición. El tiempo que tarda el pulso láser en viajar desde el láser de medición hasta el objeto y de vuelta se puede usar para calcular la distancia entre los dos puntos. Los láseres de medición se utilizan comúnmente en topografía, navegación y otras aplicaciones en las que se necesitan mediciones precisas.
ID:(481, 0)
GPS (Sistema de Posicionamiento Global)
Descripción
El Sistema de Posicionamiento Global (GPS) es un sistema de navegación basado en satélites que usa una red de 24 satélites orbitando la Tierra para determinar la ubicación exacta de una persona o objeto en el planeta. Los receptores GPS calculan la distancia a cada satélite midiendo la cantidad de tiempo que tardan las señales en viajar desde el satélite hasta el receptor. Una vez que estas distancias se conocen, el receptor puede usar un proceso llamado trilateración para calcular su ubicación exacta, incluyendo la longitud y la latitud, así como la altitud. Esto se puede usar para medir distancias entre dos ubicaciones, así como la longitud de un camino recorrido por una persona o objeto.
ID:(474, 0)
Posición en más dimensiones
Concepto
La posición o ubicación de un objeto en un sistema de más de una dimensión se define tradicionalmente mediante un vector. Este vector va desde el origen del sistema de coordenadas hasta el objeto, teniendo el mismo número de componentes que dimensiones existen.
ID:(477, 0)
Representación de la posición en una dimensión
Concepto
En un sistema de una dimensión, la posición de un objeto se puede representar mediante un escalar, el cual indica la distancia desde el origen de cero hacia la dirección en que se encuentra el objeto. Esta distancia se mide como una cantidad positiva o negativa, dependiendo de si el objeto se encuentra en la dirección positiva o negativa del eje. Esta posición se puede representar por ejemplo con el parámetro $x$ o $s$, donde los escalares $x$ o $s$ indica la distancia desde el origen a la posición del objeto.
Vector unidimensional para describir una posición
ID:(2251, 0)
Representación de la posición en dos dimensión
Concepto
En un sistema de dos dimensiones, la posición de un objeto se puede representar mediante un vector, el cual indica la distancia desde el origen de cero (coordenadas $(0,0)$) hacia la dirección en que se encuentra el objeto. Ambas coordenadas se miden como una cantidad positiva o negativa, dependiendo de si el objeto se encuentra en la dirección positiva o negativa del eje respectivo. Esta posición se puede representar por ejemplo con el parámetro $(x,y)$, donde los escalares $x$ e $y$ indican la distancia desde el origen del objeto en cada eje.
ID:(2234, 0)
Representación de la posición en tres dimensión
Concepto
En un sistema de dos dimensiones, la posición de un objeto se puede representar mediante un vector, el cual indica la distancia desde el origen de cero (coordenadas $(0,0,0)$) hacia la dirección en que se encuentra el objeto. Ambas coordenadas se miden como una cantidad positiva o negativa, dependiendo de si el objeto se encuentra en la dirección positiva o negativa del eje respectivo. Esta posición se puede representar por ejemplo con el parámetro $(x,y,z)$, donde los escalares $x$, $y$ y $z$ indican la distancia desde el origen del objeto en cada eje.
ID:(2235, 0)
Posición
Concepto
La posición ($s$) de un objeto en un sistema unidimensional se refiere a la ubicación del objeto en relación con un punto de referencia. Esta ubicación se expresa como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta en un eje cartesiano, o puede seguir un camino curvo:
ID:(15, 0)
Posición inicial
Concepto
La posición inicial ($s_0$) es la ubicación inicial de un objeto antes de que comience un movimiento. Esta ubicación se define como la distancia entre el objeto y el punto de origen. Esta distancia puede ser una línea recta sobre un eje cartesiano, o puede seguir una trayectoria curva.
ID:(10302, 0)
Distancia recorrida
Concepto
La distancia recorrida en un tiempo ($\Delta s$) por un objeto se mide midiendo la distancia entre dos puntos específicos a lo largo de una trayectoria. Esta trayectoria puede ser una línea recta en un eje cartesiano, o bien un camino curvo. La distancia se calcula midiendo la longitud de la trayectoria entre los dos puntos de partida y llegada.
ID:(9495, 0)
Distancia infinitesimal
Concepto
La distancia infinitesimal recorrida ($ds$) entre dos puntos es una medida de distancia tan pequeña que el movimiento entre ambos puntos puede ser considerado uniforme o sea a velocidad constante.
En general, las diferencias de una variable se denotan añadiendo el símbolo $\Delta$ antes de la letra correspondiente, de modo que la variación de la posición $s$ se expresa como $\Delta s$. Para variaciones infinitesimales, se utiliza una $d$ en lugar de $\Delta$, por lo que una variación infinitesimal en la posición sería $ds$.
ID:(14451, 0)
Medición de la distancia recorrida
Top
Para describir el movimiento de un objeto, es necesario calcular la distancia recorrida en un tiempo ($\Delta s$). Esta distancia se obtiene midiendo la posición inicial ($s_0$) y la posición ($s$) del objeto en cuestión. Si los movimientos son unidimensionales, la distancia recorrida se determina restando la posición inicial de la posición final.
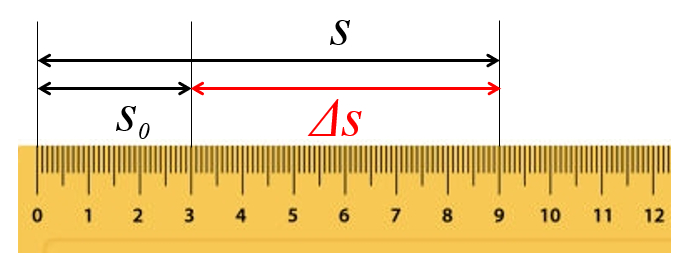
ID:(15382, 0)
Distancia recorrida en más dimensiones
Concepto
Para describir el movimiento de un objeto, es necesario considerar la distancia entre su punto inicial y su punto final. Esta distancia, sin embargo, no siempre refleja el recorrido real del objeto, ya que un camino curvo hará que el recorrido sea mayor que la distancia entre los puntos inicial y final. Si los dos puntos están muy cerca, la curvatura será despreciable y, por lo tanto, el recorrido coincide con la distancia entre ambos puntos.
En este caso hablamos de una distancia infinitesimal.
ID:(9496, 0)
Distancia infinitesimal en más dimensiones
Concepto
Para modelar el movimiento de un cuerpo es necesario describir cómo se desplaza, es decir, el camino y la dirección en que se mueve. Si el camino es curvo, el vector entre la posición actual y la futura no necesariamente coincidirá con el camino real, a menos que el camino sea infinitesimal. En dicho caso, la desviación del segmento es despreciable y el arco corresponde al vector tangencial a la curva.
ID:(14452, 0)
Modelo
Top
En lo que respecta a la posición (en el caso de escalares como la posición ($s$) y como vector la posición actual ($\vec{s}$)), se puede definir el camino recorrido. Este puede ser macroscópico (en el caso de escalares como la distancia recorrida en un tiempo ($\Delta s$) y como vector la distancia recorrida ($\Delta\vec{s}$)), lo que puede no reflejar que el camino puede no ser rectilíneo. Si nos interesa estudiar el camino real, debemos considerar variaciones infinitesimales (en el caso de escalares como la distancia infinitesimal recorrida ($ds$) y como vector el elemento de camino recorrido ($d\vec{s}$)), en las cuales, en primera aproximación, se puede considerar que es rectilíneo.
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $
&Ds = &s - &s_0
$ \Delta s \equiv s - s_0 $
Ds = s - s_0
$d\vec{s} \equiv \vec{s} - \vec{s}_0 $
d&s = &s - &s_0
$ds \equiv s - s_0 $
ds = s - s_0
ID:(15381, 0)
Distancia recorrida
Ecuación
Podemos calcular la distancia recorrida en un tiempo ($\Delta s$) a partir de la posición inicial ($s_0$) y la posición ($s$) mediante la siguiente ecuación:
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Distancia infinitesimal
Ecuación
Si se desea estudiar el movimiento de un cuerpo que se desplaza de manera no uniforme, es necesario trabajar en una escala más pequeña donde las fluctuaciones no sean relevantes. Para esto, se introduce el concepto de desplazamiento infinitesimal, el cual se calcula restando la posición actual de la posición anterior, la cual debe ser muy cercana a la primera.
Por ello se introduce la distancia infinitesimal recorrida ($ds$) como la diferencia entre la posición ($s$) y la posición inicial ($s_0$) como:
| $ds \equiv s - s_0 $ |
ID:(14450, 0)
Distancia recorrida en más dimensiones
Ecuación
Para describir el movimiento de un objeto, es fundamental calcular la distancia que ha recorrido. Para lograrlo, se definen los puntos inicial y final del objeto mediante vectores, y la distancia se calcula restando un vector del otro. Esto coincide únicamente con el camino recorrido si el desplazamiento es rectilíneo, lo cual suele ocurrir cuando ambos puntos están muy próximos, como en el caso de la distancia recorrida ($\Delta\vec{s}$) restando la posición del origen ($\vec{s}_0$) de la posición actual ($\vec{s}$):
| $ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
ID:(714, 0)
Distancia infinitesimal en más dimensiones
Ecuación
En el caso de un espacio con más de una dimensión, el camino entre dos puntos no tiene que ser necesariamente recto, como sucede en espacios unidimensionales. En este tipo de situaciones, un vector que representa la distancia entre dos puntos del camino será siempre igual o menor que la distancia real a lo largo del camino. Sin embargo, ambos coincidirán si la distancia entre los dos puntos es infinitesimal o muy pequeña. Por lo tanto, resulta útil definir el vector infinitesimal, que permite describir el comportamiento del objeto en un espacio continuo de manera precisa.
Por ello se introduce el elemento de camino recorrido ($d\vec{s}$) como la diferencia entre la posición actual ($\vec{s}$) y la posición del origen ($\vec{s}_0$) como:
| $d\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
ID:(9497, 0)