Benützer:
Position
Storyboard 
Um die Position eines Objekts zu bestimmen, wird ein Koordinatensystem eingeführt, das es ermöglicht, einen Ursprungspunkt festzulegen und die Position durch die Messung der Entfernung entlang einer geraden Linie oder einer Kurve zu definieren. Demzufolge entspricht die Einheit der Position einer Längenmessung, wie Kilometer, Meter, Zentimeter und so weiter.
Die Wahl des Koordinatensystems ist flexibel und erfolgt, um die Modellierung und die zugehörigen Berechnungen so weit wie möglich zu vereinfachen. Zum Beispiel, wenn sich das Objekt entlang einer Strecke bewegt, die nicht unbedingt gerade verläuft, ist es vorteilhaft, das Koordinatensystem entlang dieser Strecke zu definieren. In diesem speziellen Fall wird die Position als die Entfernung vom Ursprung oder dem Startpunkt der Strecke definiert.
ID:(607, 0)
Mechanismen
Iframe
Eine der wichtigsten Variablen zur Beschreibung der Bewegung eines Körpers ist seine Position. Diese kann entweder ein Skalar sein, der die Entfernung zu einem Bezugspunkt in eindimensionalen Situationen definiert, oder ein Vektor mit einem Ursprung in mehrdimensionalen Fällen.
Mechanismen
ID:(15380, 0)
Referenz zur Längenmessung
Konzept
Jede Messung entspricht einem Vergleich eines bestimmten Werts mit einem Referenzmuster, woraus der Wert in der entsprechenden Einheit abgeleitet wird.
Im Laufe der Zeit haben sich diese Muster weiterentwickelt und eine größere Genauigkeit erreicht. Beispiele sind:
Gefälschte Kopie des ersten Metermaßstabs (beachten Sie die falsche Schreibweise), versiegelt im Fundament eines Gebäudes, 36 rue de Vaugirard, Paris, Ken Eckert (Wikimedia Commons)
Eine Kopie des vorläufigen Meters, installiert von 1796 bis 1797, an der Wand eines Gebäudes in der 36 Rue de Vaugirard, Paris
Historische niederländische Nachbildungen metrischer Maßstäbe in der Sammlung des Rijksmuseums, Amsterdam: Eisenzähler mit Gehäuse (konstruiert von Étienne Lenoir, 1799; Katalognummer NG-2001-16-C-8), Kupfergrab-Kilogramm mit Gehäuse (1798; Katalognummer NG-2001-16-D-9), Kupfer-Volumenmaße ( 1829; Katalognummer NG-2001-16-B-28)., Yerpo (Wikimedia Commons)
Im Jahr 1799 fertigte Étienne Lenoir die Platin- und zwölf Eisenstandards des Meters an.
Rule (Geändert von Wikimedia Commons, Ein Lineal, das zwei übliche Längeneinheiten darstellt, den Zentimeter und den Zoll)
Das Gradmesser enthält eine längsgraduierte Skala aus rostfreiem Stahl, um zu verhindern, dass die Bildung von Rost das Lesen beeinträchtigt oder die Skala löscht.
ID:(2238, 0)
Methode der Längenmessung
Konzept
Es gibt viele Methoden zur Messung von Distanzen, einschließlich:
1. Lineal oder Bandmaß: Dies ist eine einfache und häufig verwendete Methode zur Messung kleiner Distanzen. Hierbei wird das Lineal oder Bandmaß direkt an dem zu messenden Objekt angelegt und die Länge abgelesen.
2. Tachometer: Ein Tachometer ist ein Gerät, das die von einem Fahrzeug oder einem anderen beweglichen Objekt zurückgelegte Distanz misst. Es funktioniert, indem es die Anzahl der Umdrehungen eines Rades oder eines anderen beweglichen Teils zählt.
3. Laser-Entfernungsmesser: Ein Laser-Entfernungsmesser verwendet einen Laserstrahl, um die Distanz zwischen dem Gerät und dem Ziel zu bestimmen. Es misst die Zeit, die der Laserstrahl benötigt, um von dem Ziel zurückzuprallen und zum Gerät zurückzukehren.
4. GPS (Global Positioning System): GPS ist ein satellitengestütztes System, das zur Bestimmung der Position und der Distanz zwischen zwei Punkten auf der Erdoberfläche verwendet werden kann. Es funktioniert, indem es die Position eines GPS-Empfängers anhand von Signalen mehrerer GPS-Satelliten trianguliert.
Dies sind nur einige Beispiele für Methoden zur Messung von Distanzen, und es gibt viele andere Techniken und Geräte, die je nach spezifischer Anwendung und gewünschter Präzision verwendet werden können.
ID:(472, 0)
Lineal oder Maßband
Beschreibung
Ein Lineal oder ein Maßband sind beide Methoden zur Messung von Längen. Ein Lineal ist ein flaches Messgerät, das mit Längeneinheiten wie Zoll, Zentimeter oder Millimeter markiert ist. Ein Maßband ist ein flexibles Messgerät, das mit Längeneinheiten markiert ist. Maßbänder sind in der Regel genauer als Lineale, da sie gekrümmte Oberflächen messen und auf größere Längen ausgedehnt werden können.
ID:(12508, 0)
Tachometer
Beschreibung
Ein Tachometer ist ein Gerät, das zur Messung der von einem Fahrzeug zurückgelegten Entfernung verwendet wird. Er befindet sich normalerweise auf dem Armaturenbrett oder Instrumentenpanel eines Autos und kann verwendet werden, um die insgesamt zurückgelegte Entfernung zu verfolgen. Ein Tachometer zählt die Umdrehungen einer Antriebswelle, die mit den Rädern des Fahrzeugs verbunden ist. Wenn das Fahrzeug sich bewegt, dreht sich die Antriebswelle, und jede Umdrehung der Antriebswelle wird gezählt und auf dem Tachometer aufgezeichnet. Der Tachometer ist in der Regel so kalibriert, dass er Entfernungen, die in Meilen oder Kilometern zurückgelegt wurden, genau messen kann.
ID:(480, 0)
Laser-Entfernungsmesser
Beschreibung
Ein Laserentfernungsmesser ist ein Gerät, das einen Laserstrahl verwendet, um die Entfernung zwischen zwei Punkten zu messen. Es funktioniert, indem es einen Laserimpuls sendet, der von dem zu messenden Objekt reflektiert und dann vom Entfernungsmesser detektiert wird. Die Zeit, die der Laserimpuls benötigt, um von dem Entfernungsmesser zum Objekt und zurück zu reisen, kann dann verwendet werden, um die Entfernung zwischen den beiden Punkten zu berechnen. Laserentfernungsmesser werden häufig in Vermessungen, Navigation und anderen Anwendungen eingesetzt, in denen präzise Messungen erforderlich sind.
ID:(481, 0)
GPS (Global Positioning System)
Beschreibung
Das Global Positioning System (GPS) ist ein satellitengestütztes Navigationssystem, das ein Netzwerk von 24 Satelliten verwendet, die die Erde umkreisen, um die exakte Position einer Person oder eines Objekts auf dem Planeten zu bestimmen. GPS-Empfänger berechnen die Entfernung zu jedem Satelliten, indem sie die Zeit messen, die die Signale benötigen, um vom Satelliten zum Empfänger zu gelangen. Sobald diese Entfernungen bekannt sind, kann der Empfänger einen Prozess namens Trilateration verwenden, um seine exakte Position, einschließlich Längen- und Breitengrad sowie Höhe, zu berechnen. Dies kann verwendet werden, um die Entfernungen zwischen zwei Standorten zu messen, sowie die Länge einer von einer Person oder einem Objekt zurückgelegten Strecke.
ID:(474, 0)
Position in mehr Dimensionen
Konzept
Die Position oder der Standort eines Objekts in einem System mit mehr als einer Dimension wird traditionell durch einen Vektor definiert. Dieser Vektor geht vom Ursprung des Koordinatensystems zum Objekt und hat dieselbe Anzahl von Komponenten wie es Dimensionen gibt.
ID:(477, 0)
Positionsdarstellung in einer Dimension
Konzept
In einem eindimensionalen System kann die Position eines Objekts durch einen Skalar repräsentiert werden, der die Entfernung vom Ursprung null in die Richtung, in der sich das Objekt befindet, angibt. Diese Entfernung wird als positive oder negative Größe gemessen, abhängig davon, ob sich das Objekt in der positiven oder negativen Richtung des Achsenabschnitts befindet. Diese Position kann beispielsweise durch den Parameter $x$ oder $s$ dargestellt werden, wobei die Skalare $x$ oder $s$ die Entfernung vom Ursprung zur Position des Objekts anzeigen.
Eindimensionaler Vektor zur Beschreibung einer Position
ID:(2251, 0)
Darstellung der Position in zwei Dimensionen
Konzept
In einem zweidimensionalen System kann die Position eines Objekts durch einen Vektor dargestellt werden, der die Entfernung vom Ursprung von Null (Koordinaten $(0,0)$) in die Richtung angibt, in der sich das Objekt befindet. Beide Koordinaten werden als positive oder negative Menge gemessen, abhängig davon, ob sich das Objekt in der positiven oder negativen Richtung des jeweiligen Achsens befindet. Diese Position kann zum Beispiel durch den Parameter $(x,y)$ dargestellt werden, wobei die Skalare $x$ und $y$ die Entfernung vom Ursprung des Objekts in jeder Achse angeben.
ID:(2234, 0)
Darstellung der Position in drei Dimensionen
Konzept
In einem zweidimensionalen System kann die Position eines Objekts durch einen Vektor dargestellt werden, der die Entfernung vom Ursprung von Null (Koordinaten $(0,0,0)$) in die Richtung angibt, in der sich das Objekt befindet. Beide Koordinaten werden als positive oder negative Menge gemessen, abhängig davon, ob sich das Objekt in der positiven oder negativen Richtung des jeweiligen Achsens befindet. Diese Position kann zum Beispiel durch den Parameter $(x,y,z)$ dargestellt werden, wobei die Skalare $x$, $y$ und $z$ die Entfernung vom Ursprung des Objekts in jeder Achse angeben.
ID:(2235, 0)
Position
Konzept
Die Position ($s$) eines Objekts in einem eindimensionalen System bezieht sich auf den Standort des Objekts in Bezug auf einen Referenzpunkt. Diese Lage wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt ausgedrückt. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekrümmten Pfad folgen.
ID:(15, 0)
Ausgangsposition
Konzept
Die Ausgangsstellung ($s_0$) ist der Startort eines Objekts, bevor sich dieses bewegt. Diese Position wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt definiert. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekrümmten Pfad folgen.
ID:(10302, 0)
Zurückgelegte Strecke
Konzept
Die Zurückgelegte Strecke in einer Zeit ($\Delta s$) eines Objekts wird gemessen, indem man die Entfernung zwischen zwei spezifischen Punkten entlang einer Trajektorie misst. Diese Trajektorie kann eine Gerade auf einem kartesischen Koordinatensystem oder ein gekrümmter Pfad sein. Die Entfernung wird berechnet, indem man die Länge der Trajektorie zwischen den beiden Start- und Endpunkten misst.
ID:(9495, 0)
Infinitesimalen Entfernung
Konzept
Die Infinitesimal zurückgelegte Strecke ($ds$) zwischen zwei Punkten ist ein Abstand, der so klein ist, dass sich die Bewegung zwischen den beiden Punkten als gleichförmig betrachtet werden kann.
Allgemein werden Differenzen einer Variablen dadurch dargestellt, dass dem entsprechenden Buchstaben das Symbol $\Delta$ vorangestellt wird. Die Veränderung der Position $s$ wird also als $\Delta s$ ausgedrückt. Für infinitesimale Veränderungen wird anstelle von $\Delta$ ein $d$ verwendet, sodass eine infinitesimale Veränderung in der Position als $ds$ dargestellt wird.
ID:(14451, 0)
Messung der zurückgelegten Strecke
Top
Um die Bewegung eines Objekts zu beschreiben, müssen wir die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnen. Diese Distanz wird gemessen, indem die Ausgangsstellung ($s_0$) und die Position ($s$) von diesem Objekt gemessen werden. Wenn die Bewegungen eindimensional sind, wird die zurückgelegte Strecke durch Subtrahieren der Anfangsposition von der Endposition bestimmt.
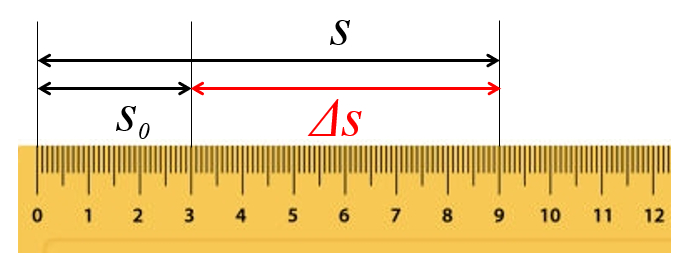
ID:(15382, 0)
Zurückgelegte Distanz in mehr Dimensionen
Konzept
Um die Bewegung eines Objekts zu beschreiben, berechnen wir die Differenz zwischen einem Startpunkt und einem Endpunkt. Diese Differenz, genannt Entfernung, entspricht jedoch nicht immer der tatsächlichen Strecke, die das Objekt zurückgelegt hat, wenn der Weg gekrümmt ist. Die Krümmung des Weges führt dazu, dass die zurückgelegte Strecke größer ist als die Entfernung zwischen den beiden Punkten. Wenn die beiden Punkte sehr nah beieinander liegen, ist die Krümmung vernachlässigbar und die zurückgelegte Strecke entspricht der Entfernung zwischen den beiden Punkten.
In diesem Fall sprechen wir von einer infinitesimalen Entfernung.
ID:(9496, 0)
Infinitesimalen Entfernung in mehr Dimensionen
Konzept
Um die Bewegung eines Körpers zu modellieren, ist es notwendig zu beschreiben, wie er sich bewegt, das heißt den Weg und die Richtung, in die er sich bewegt. Wenn der Weg gekrümmt ist, stimmt der Vektor zwischen der aktuellen und zukünftigen Position nicht notwendigerweise mit dem tatsächlichen Weg überein, es sei denn, der Weg ist infinitesimal. In einem solchen Fall ist die Abweichung von dem Segment vernachlässigbar, und der Bogen entspricht dem tangentialen Vektor der Kurve.
ID:(14452, 0)
Modell
Top
Hinsichtlich der Position (im Falle von Skalaren wie die Position ($s$) und als Vektor wie die Aktuelle Position ($\vec{s}$)) kann der zurückgelegte Weg definiert werden. Dieser kann makroskopisch sein (im Falle von Skalaren wie die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und als Vektor wie die Entfernung Run ($\Delta\vec{s}$)), was möglicherweise nicht widerspiegelt, dass der Weg nicht geradlinig sein kann. Wenn wir daran interessiert sind, den tatsächlichen Weg zu untersuchen, müssen wir infinitesimale Variationen berücksichtigen (im Falle von Skalaren wie die Infinitesimal zurückgelegte Strecke ($ds$) und als Vektor wie der Wegelement zurückgelegt ($d\vec{s}$)), bei denen, in einer ersten Näherung, davon ausgegangen werden kann, dass er geradlinig ist.
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $
&Ds = &s - &s_0
$ \Delta s \equiv s - s_0 $
Ds = s - s_0
$d\vec{s} \equiv \vec{s} - \vec{s}_0 $
d&s = &s - &s_0
$ds \equiv s - s_0 $
ds = s - s_0
ID:(15381, 0)
Zurückgelegten Strecke
Gleichung
Wir können die Zurückgelegte Strecke in einer Zeit ($\Delta s$) aus die Ausgangsstellung ($s_0$) und die Position ($s$) berechnen mit der folgenden Gleichung:
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 0)
Infinitesimalen Entfernung
Gleichung
Wenn man die Bewegung eines Körpers, der sich ungleichmäßig bewegt, studieren möchte, ist es notwendig, auf einer kleineren Skala zu arbeiten, auf der Fluktuationen nicht relevant sind. Zu diesem Zweck wird das Konzept der infinitesimalen Verschiebung eingeführt, die berechnet wird, indem die aktuelle Position von der vorherigen Position abgezogen wird, die sehr nahe an der ersten sein muss.
Daher wird die Infinitesimal zurückgelegte Strecke ($ds$) als die Differenz zwischen die Position ($s$) und die Ausgangsstellung ($s_0$) eingeführt als:
| $ds \equiv s - s_0 $ |
ID:(14450, 0)
Zurückgelegten Strecke in mehr Dimensionen
Gleichung
Um die Bewegung eines Objekts zu beschreiben, ist es notwendig, die zurückgelegte Strecke zu berechnen. Dazu werden die Anfangs- und Endpunkte des Objekts mithilfe von Vektoren definiert, und die Entfernung wird berechnet, indem ein Vektor vom anderen subtrahiert wird. Dies entspricht nur dem zurückgelegten Weg, wenn die Verschiebung geradlinig ist, was in der Regel der Fall ist, wenn beide Punkte sehr nah beieinander liegen, wie im Fall von die Entfernung Run ($\Delta\vec{s}$), wobei die Position von Ursprung ($\vec{s}_0$) von die Aktuelle Position ($\vec{s}$) subtrahiert wird:
| $ \Delta\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
ID:(714, 0)
Infinitesimalen Entfernung in mehr Dimensionen
Gleichung
Im Falle eines Raums mit mehr als einer Dimension muss der Weg zwischen zwei Punkten nicht zwangsläufig gerade verlaufen, wie es in eindimensionalen Räumen der Fall ist. In solchen Situationen wird ein Vektor, der die Entfernung zwischen zwei Punkten entlang des Weges darstellt, immer gleich oder kleiner als die tatsächliche Entfernung entlang des Weges sein. Wenn jedoch der Abstand zwischen den beiden Punkten infinitesimal oder sehr klein ist, werden beide übereinstimmen. Daher ist es nützlich, den infinitesimalen Vektor zu definieren, der es uns ermöglicht, das Verhalten eines Objekts in einem kontinuierlichen Raum präzise zu beschreiben.
Daher wird der Wegelement zurückgelegt ($d\vec{s}$) als die Differenz zwischen die Aktuelle Position ($\vec{s}$) und die Position von Ursprung ($\vec{s}_0$) eingeführt als:
| $d\vec{s} \equiv \vec{s} - \vec{s}_0 $ |
ID:(9497, 0)