Utilizador:
Posição em uma dimensão
Storyboard
Para definir a posição de um objeto, introduz-se um sistema de coordenadas que permite estabelecer um ponto de origem e definir a posição medindo a distância ao longo de uma linha reta ou uma curva. Como resultado, a unidade de posição corresponde a uma medida de comprimento, como quilômetros, metros, centímetros, e assim por diante.
A escolha do sistema de coordenadas é flexível e é feita para simplificar ao máximo a modelagem e os cálculos associados. Por exemplo, se o objeto se move ao longo de uma trilha, que não necessariamente é reta, é vantajoso definir o sistema de coordenadas ao longo dessa trilha. Nesse caso específico, a posição é definida como a distância a partir da origem ou do ponto de partida da trilha.
ID:(607, 'ky')
Posição, uma dimensão
Storyboard
Um dos aspectos fundamentais da física é determinar a posição dos objetos que analisamos. Este simulador permite explorar esse conceito: ao gerar uma barra vermelha e mover o mouse, é possível determinar seu comprimento. Esse comprimento corresponde à posição da borda direita em relação a uma origem situada na borda esquerda.
Observe o painel do simulador:
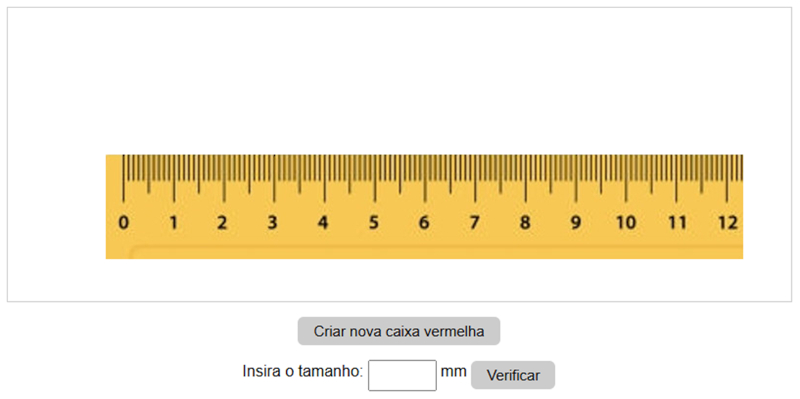
Crie uma caixa vermelha pressionando o botão localizado abaixo da régua.
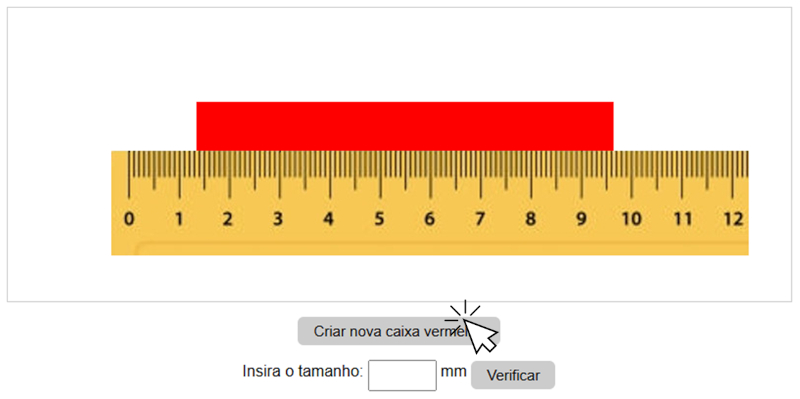
Em seguida, arraste-a mantendo pressionado o botão esquerdo do mouse.
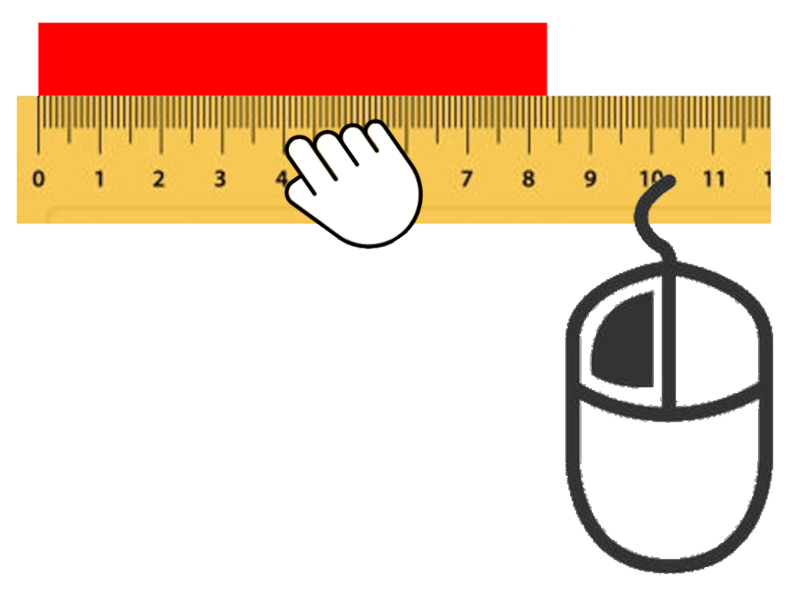
Certifique-se de que esteja corretamente alinhada com o zero da régua no lado esquerdo da caixa.
Leia o valor indicado na borda direita.
Insira o valor estimado no campo inferior (valores fracionários são permitidos).
Se o valor estiver correto, será confirmada a medição. Caso contrário, o valor correto será mostrado.
Você pode experimentar movendo a origem para a esquerda e observar como um pequeno desalinhamento inicial gera um erro no resultado final. Também pode ajustar o valor inserido ele será considerado correto desde que esteja dentro de uma margem de um milímetro.
Se alguém nos disser que está a 45 km de distância, surge imediatamente a pergunta: a partir de onde? Ou seja, precisamos conhecer a origem que dá sentido a essa informação.
No simulador, isso se traduz na necessidade de posicionar o zero da régua no lado esquerdo da caixa vermelha para determinar corretamente a posição do lado direito.
Se isso não for feito com cuidado, o valor lido na régua no lado direito será incorreto e a simulação mostrará que a medição foi feita de forma errada:
Ao posicionar a régua na origem, percebemos imediatamente como é difícil alinhar exatamente o zero com a borda esquerda. Algo semelhante acontece na borda direita, que cai entre duas marcas da régua, obrigando-nos a estimar seu valor:
No final, estimamos a fração do espaço preenchido e atribuímos um valor com precisão de décimos de milímetro. No entanto, percebemos que estamos operando nesse nível sem sequer considerar os centésimos.
Concluímos, portanto, que todo instrumento de medição (não apenas os de comprimento) possui uma limitação inerente. Por essa razão, os valores obtidos em uma medição devem sempre ser expressos juntamente com sua incerteza. Isso pode ser feito associando o número a um intervalo, como por exemplo: [27,1, 27,7], ou utilizando o valor médio (27,4) e indicando quanto deve ser somado ou subtraído para obter o intervalo:
27,4±0,3
Essa prática se aplica não apenas a medições individuais, mas também ao cálculo de distâncias, como mostrado no modelo por meio de um exemplo.
ID:(3, 0)
Posição em uma dimensão
Descrição
Para definir a posição de um objeto, introduz-se um sistema de coordenadas que permite estabelecer um ponto de origem e definir a posição medindo a distância ao longo de uma linha reta ou uma curva. Como resultado, a unidade de posição corresponde a uma medida de comprimento, como quilômetros, metros, centímetros, e assim por diante. A escolha do sistema de coordenadas é flexível e é feita para simplificar ao máximo a modelagem e os cálculos associados. Por exemplo, se o objeto se move ao longo de uma trilha, que não necessariamente é reta, é vantajoso definir o sistema de coordenadas ao longo dessa trilha. Nesse caso específico, a posição é definida como a distância a partir da origem ou do ponto de partida da trilha.
ID:(607, 0)