User:
Instant Acceleration
Storyboard 
To describe how speed evolves over time, the variation in time must be studied.
The ratio of the variation of the velocity is equivalent to the variation of the velocity in the elapsed time which, divided by this, corresponds to the acceleration.
For an infinitesimal elapsed time the acceleration corresponds to the instantaneous acceleration.
ID:(1433, 0)
Mechanisms
Iframe
On one hand, it's important to differentiate between the simplest, one-dimensional case and the multi-dimensional one. For both cases, the derivative of the speed ($v$) with respect to the time ($t$), which corresponds to the slope of the curve of the speed ($v$), is equal to the instant acceleration ($a$). Similarly, the derivative of the speed (Vector) ($\vec{v}$) with respect to the time ($t$), which corresponds to the speed (Vector) ($\vec{v}$).
Mechanisms
ID:(15398, 0)
Instant acceleration
Concept
Acceleration is defined as the change in velocity per unit of time. However, this definition refers to the average acceleration that exists during a given time interval.
This limitation of average acceleration is reflected in situations where an object accelerates and then decelerates to a stop. In this case, the average acceleration is zero, which suggests that the object has not accelerated at all. However, this is not true as the object moves both during the acceleration phase and the deceleration phase.
To determine the acceleration at each instant, a small enough time interval must be considered, such that the acceleration can be assumed to be approximately constant during that time. Thus, the average acceleration estimated in this way equals the acceleration present at the instant being considered.
Therefore, the term 'instantaneous acceleration' is used to refer to the acceleration at a particular moment.
ID:(11352, 0)
Acceleration as a derivative
Concept
If we take the time elapsed ($\Delta t$) and observe an object in motion with velocity the speed ($v$), and then observe the same object at a later time $t+\Delta t$ with velocity $v(t+\Delta t)$, we can estimate its acceleration as the change in velocity during the time elapsed ($\Delta t$):
$a\sim\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}$
As the value of $\Delta t$ decreases, this expression for acceleration approaches the instantaneous rate of change of velocity at time $t$, or in other words, the slope of the tangent line to the velocity curve at that point:
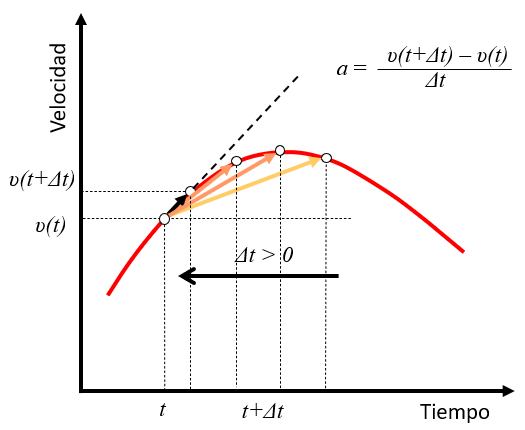
This generalizes the concept of the instant acceleration ($a$) for the case of the constant Acceleration ($a_0$), as seen earlier, expressed as the derivative of the speed ($v$) with respect to the time ($t$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
ID:(11353, 0)
Path traveled as area under speed curve
Concept
If one observes that the speed ($v$) is equal to the distance traveled in a time ($\Delta s$) per the time elapsed ($\Delta t$), it indicates that the path is given by:
$\Delta s = v\Delta t$
Since the product $v\Delta t$ represents the area under the velocity versus time curve, which is also equal to the traveled path:
This area can also be calculated with the integral of the corresponding function. Therefore, the integral of the acceleration between the start Time ($t_0$) and the time ($t$) corresponds to the change in velocity between the initial velocity the initial Speed ($v_0$) and the speed ($v$):
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
ID:(2252, 0)
Curvature of the position curve over time
Concept
The instant acceleration ($a$) is equal to the derivative of the speed ($v$) with respect to the time ($t$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
And since the speed ($v$) is the derivative of the position ($s$) with respect to the time ($t$):
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Therefore, the instant acceleration ($a$) is the second derivative of the position ($s$) with respect to the time ($t$),
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
which corresponds to the curvature of the curve the position ($s$) as a function of the time ($t$):
ID:(11354, 0)
Model
Top
In the case of one dimension, the instant acceleration ($a$) is related to the speed ($v$) through its derivative at the time ($t$), while the integral of the instant acceleration ($a$) over the interval from the time ($t$) to the start Time ($t_0$) provides the speed ($v$) from the initial Speed ($v_0$). In a more general context, in more than one dimension, the function the speed (Vector) ($\vec{v}$) can be derived at the time ($t$), resulting in the speed (Vector) ($\vec{v}$).
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$
&a = @DIF( &v , t , 1)
$ a =\displaystyle\frac{ d v }{ d t }$
a = @DIF( v , t , 1)
$ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$
a = @DIFF( s , t , 2 )
$ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $
v = v_0 + @INT( a, tau, t_0, t )
ID:(15401, 0)
Instantaneous acceleration in one dimension
Equation
The variable the mean Acceleration ($\bar{a}$), calculated as the change in the speed Diference ($\Delta v$) divided by the interval of the time elapsed ($\Delta t$) through
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
is an approximation of the actual acceleration, which tends to distort when the acceleration fluctuates during the time interval. Therefore, the concept of the instant acceleration ($a$) determined over a very small time interval is introduced. In this case, we are referring to an infinitesimally small time interval, and the variation of velocity over time reduces to the derivative of the speed ($v$) with respect to the time ($t$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
If we consider the difference in the speed ($v$) at times $t+\Delta t$ and $t$:
$\Delta v = v(t+\Delta t)-v(t)$
and take $\Delta t$ as the time elapsed ($\Delta t$), then in the limit of infinitesimally short times:
$a=\displaystyle\frac{\Delta v}{\Delta t}=\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t} \rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}=\displaystyle\frac{dv}{dt}$
This last expression corresponds to the derivative of the function the speed ($v$):
| $ a =\displaystyle\frac{ d v }{ d t }$ |
which, in turn, is the slope of the graphical representation of that function at the time ($t$).
which corresponds to the derivative of velocity.
ID:(4356, 0)
Acceleration integration
Equation
If the instant acceleration ($a$) corresponds to the derivative of the speed ($v$) at the time ($t$),
| $ a =\displaystyle\frac{ d v }{ d t }$ |
then the speed ($v$) equals the initial Speed ($v_0$), and the integration of the acceleration from the start Time ($t_0$) to the time ($t$) is:
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
If we integrate the definition of the instant acceleration ($a$) at the time ($t$),
| $ a =\displaystyle\frac{ d v }{ d t }$ |
this means that for a time interval $dt$, the distance traveled is
$dv = a dt$
If we consider $N$ intervals $dt_i$ with accelerations $a_i$, the total change in velocity will be
$v - v_0 = \displaystyle\sum_i a_i dt_i$
If we consider the acceleration-time curve, the elements $a_i dt_i$ correspond to rectangles with height $a_i$ and width $dt_i$. The sum, therefore, corresponds to the area under the acceleration-time curve. Hence, the sum can be expressed as an integral:
| $ v = v_0 +\displaystyle\int_{t_0}^t a d\tau $ |
ID:(10307, 0)
Instantaneous acceleration as a function of position
Equation
Since the instant acceleration ($a$) represents the slope of the speed ($v$) with respect to the time ($t$),
| $ a =\displaystyle\frac{ d v }{ d t }$ |
and the speed ($v$) is the slope of the position ($s$) with respect to the time ($t$),
| $ v =\displaystyle\frac{ d s }{ d t }$ |
we can express the instant acceleration ($a$) as the second derivative of the position ($s$) with respect to the time ($t$).
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
Given that the instant acceleration ($a$) is the derivative of the speed ($v$) with respect to the time ($t$),
| $ a =\displaystyle\frac{ d v }{ d t }$ |
and the speed ($v$) is the derivative of the position ($s$) with respect to the time ($t$),
| $ v =\displaystyle\frac{ d s }{ d t }$ |
we have
$a=\displaystyle\frac{dv}{dt}=\displaystyle\frac{d}{dt}\displaystyle\frac{ds}{dt}=\displaystyle\frac{d^2s}{dt^2}$
therefore,
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
ID:(12572, 0)
Instant acceleration in more dimensions
Equation
In general, velocity should be understood as a three-dimensional vector. That is to say, its the position ($s$) needs to be described by a vector a posición (vector) ($\vec{s}$), for which each component the speed ($v$) can be defined as shown in the following equation:
| $ a =\displaystyle\frac{ d v }{ d t }$ |
This allows for the generalization of the speed (Vector) ($\vec{v}$) as follows:
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
As a vector can be expressed as an array of its different components,
$\vec{v}=(v_x,v_y,v_z)$
its derivative can be expressed as the derivative of each of its components:
$\displaystyle\frac{d}{dt}\vec{v}=\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=\left(\displaystyle\frac{dv_x}{dt},\displaystyle\frac{dv_y}{dt},\displaystyle\frac{dv_z}{dt}\right)=\displaystyle\frac{d\vec{v}}{dt}=\vec{a}$
So, in general, instantaneous velocity in more than one dimension is:
| $ \vec{a} = \displaystyle\frac{ d\vec{v} }{ dt }$ |
ID:(3155, 0)