User:
Instantaneous speed
Storyboard 
If the speed varies over time, the ratio between the distance traveled and the time elapsed becomes the average speed.
To determine the speed at a specific moment, it must be estimated over a time interval so short that it remains nearly constant. This is known as instantaneous speed and corresponds to the derivative of the position with respect to time.
ID:(1432, 0)
Mechanisms
Iframe
On one hand, it's important to differentiate between the simplest case, which is one-dimensional, and the more complex case involving more than one dimension. In both cases, the derivative of the position ($s$) with respect to the time ($t$), which corresponds to the slope of the curve of the position ($s$), is equal to the speed ($v$). Similarly, the derivative of the posición (vector) ($\vec{s}$) with respect to the time ($t$), corresponds to the speed (Vector) ($\vec{v}$).
On the other hand, the area under the curve of the speed ($v$) at the time ($t$), which corresponds to integration, allows us to calculate the position ($s$).
Mechanisms
ID:(15393, 0)
Instant speed
Concept
The speed ($v$) is defined as the displacement per unit of time. However, this concept is reduced to ($$) that exists during the interval of time considered.
The limitation of the average velocity is reflected in the assumption that an object instantly goes from rest to a given velocity. It is as if a bus that has just left the terminal suddenly reaches cruising speed, which is totally absurd. The velocity evolves, increases, decreases (due to a traffic light or picking up passengers), and slowly increases until it reaches a more or less constant value when traveling on the road. Therefore, a bus that normally travels on the road at around 100 km/h will take more than 8 hours to cover 800 km because the fluctuations in velocity must be taken into account. In the end, it will have taken 10 hours to cover 800 km traveling at an average speed of 80 km/h.
If we want to know the velocity at each moment, we must take a time interval so small that during this time, the velocity can be considered approximately constant. Thus, the average velocity estimated in this way is equivalent to the velocity that exists at the considered moment.
That's why we talk about instantaneous velocity.
ID:(16, 0)
Speed as a derivative
Concept
If we take ($$) with ($$) ($s(t)$) and observe a point at a future time $t+\Delta t$ with a position $s(t+\Delta t)$, we can estimate the velocity as the distance traveled in the time $\Delta t$:
$s(t+\Delta t)-s(t)$
the speed ($v$) can be calculated by dividing the distance traveled by the elapsed time:
$v\sim\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}$
As the value of $\Delta t$ becomes smaller, the calculated velocity approaches the tangent to the position curve at the time:
This generalizes what had already been seen for the case of constant velocity.
ID:(1638, 0)
Path as integral of speed
Concept
The integral of the speed ($v$) corresponds to the area under the curve that defines this function. Therefore, the integral of the velocity between the start Time ($t_0$) and the time ($t$) corresponds to the distance traveled between the starting position ($s_0$) and the position ($s$).
Therefore, we have:
| $ s = s_0 +\displaystyle\int_{t_0}^t v d\tau$ |
Which is represented in the following graph:
I walk as an area under the speed and time curve.
ID:(2242, 0)
Concept more dimensions
Top
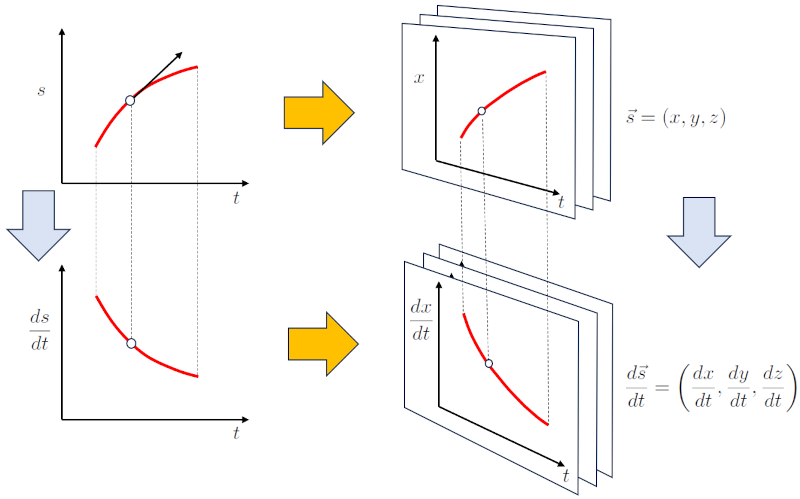
For motions occurring in more than one dimension, the description of motion in one dimension must be generalized. This is achieved by working with a multi-dimensional version for the position. In the case of three dimensions, this is:
$s \rightarrow \vec{s} = (x, y, z)$
Similarly, the derivative of the vector with respect to time can be defined, resulting in the velocity vector:
$v=\displaystyle\frac{ds}{dt} \rightarrow \displaystyle\frac{d\vec{s}}{dt} = \left(\displaystyle\frac{dx}{dt}, \displaystyle\frac{dy}{dt}, \displaystyle\frac{dz}{dt}\right) = (v_x, v_y, v_z) = \vec{v}$
This is summarized in the following graphical representation:
ID:(15506, 0)
Model
Top
In the case of one dimension, the speed ($v$) is related to the position ($s$) through its derivative at the time ($t$), while the integral of the speed ($v$) over the interval from the time ($t$) to the start Time ($t_0$) provides the position ($s$) from the starting position ($s_0$). In a more general context, in more than one dimension, the function the posición (vector) ($\vec{s}$) can be derived at the time ($t$), resulting in the speed (Vector) ($\vec{v}$)
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \vec{ v } =\displaystyle\frac{d \vec{s} }{d t }$
&v = @DIFF( &s , t , 1)
$ s = s_0 +\displaystyle\int_{t_0}^t v d\tau$
s = s_0 + @INT( v, tau, t_0, t)
$ v =\displaystyle\frac{ d s }{ d t }$
v = ds / dt
ID:(15391, 0)
Instantaneous speed in one dimension
Equation
The instantaneous speed ($v$), determined by the relationship between the infinitesimal distance traveled ($ds$) and the infinitesimal Variation of Time ($dt$), provides a more accurate estimate of the actual velocity at any moment of the time ($t$), compared to the mean Speed ($\bar{v}$), which is calculated from the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$) using the equation:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
This is achieved through the derivative of position with respect to time, i.e.,:
| $ v =\displaystyle\frac{ d s }{ d t }$ |
If we consider the distance traveled as the difference in position between time $t+\Delta t$ and time $t$:
$\Delta s = s(t+\Delta t)-s(t)$
and take $\Delta t$ as the elapsed time, then in the limit of infinitesimally short times, the average velocity can be expressed as:
$v_m=\displaystyle\frac{\Delta s}{\Delta t}=\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}\rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{s(t+\Delta t)-s(t)}{\Delta t}=\displaystyle\frac{ds}{dt}$
This last expression corresponds to the derivative of the position function $s(t)$:
| $ v =\displaystyle\frac{ d s }{ d t }$ |
which in turn is the slope of the graphical representation of this function over time.
Thus, the instantaneous velocity the speed ($v$) of the position ($s$) is known at any instant of the time ($t$) with greater precision.
ID:(3153, 0)
Speed integration
Equation
Given that velocity corresponds to the temporal derivative of position,
| $ v =\displaystyle\frac{ d s }{ d t }$ |
the integration of velocity corresponds to the distance traveled.
| $ s = s_0 +\displaystyle\int_{t_0}^t v d\tau$ |
In the definition of velocity, integrating over time yields
| $ v =\displaystyle\frac{ d s }{ d t }$ |
which means that over a time interval
$ds = v dt$
If we consider
$s - s_0 = \displaystyle\sum_i v_i dt_i$
In the velocity-time curve, the elements
| $ s = s_0 +\displaystyle\int_{t_0}^t v d\tau$ |
ID:(10308, 0)
Instant speed in more dimensions
Equation
In general, velocity should be understood as a three-dimensional entity, that is, a vector. Its position is described by a position vector
| $ v =\displaystyle\frac{ d s }{ d t }$ |
This allows for the generalization of velocity:
| $ \vec{ v } =\displaystyle\frac{d \vec{s} }{d t }$ |
As a vector, velocity can be expressed as an array of its different components:
$\vec{v}=\begin{pmatrix}v_x\v_y\v_z\end{pmatrix}$
And its derivative can be expressed as the derivative of each of its components:
$\displaystyle\frac{d\vec{v}}{dt}=\begin{pmatrix}\displaystyle\frac{d v_x}{dt}\displaystyle\frac{d v_y}{dt}\displaystyle\frac{d v_z}{dt}\end{pmatrix}=\begin{pmatrix}a_x\a_y\a_z\end{pmatrix}=\vec{a}$
Thus, in general, the instantaneous velocity in more than one dimension is a vector with components in each of the directions:
| $ \vec{ v } =\displaystyle\frac{d \vec{s} }{d t }$ |
ID:(4354, 0)