User:
Constant speed, two stages
Storyboard 
If during a motion at constant speed a change occurs, it results in a movement that occurs in two stages, each characterized by a defined velocity.
Each stage is modeled with a linear relationship represented by a line, where the key is that the final time and position of the first stage are, in turn, the initial time and position of the second stage.
It is important to note that this model has a problem since the velocity changes instantaneously, which equates to an acceleration followed by infinite deceleration, which is not realistic. However, this problem is not relevant if the duration of the stages is much longer than the time in which the velocity change occurs.
ID:(1448, 0)
Mechanisms
Iframe
In the first stage, if the velocity is constant, a direct relationship of the first stage speed ($v_1$) is established between the first final position and started second stage ($s_1$) and the final time of first and start of second stage ($t_1$), represented by a straight line.
In the second stage, null initial positions and times cannot be defined, as they must correspond to the first final position and started second stage ($s_1$) and the final time of first and start of second stage ($t_1$). Since the velocity is constant in this stage, a direct relationship of the second stage speed ($v_2$) is established between the second stage final position ($s_2$) and the second stage ending time ($t_2$), represented by another straight line.
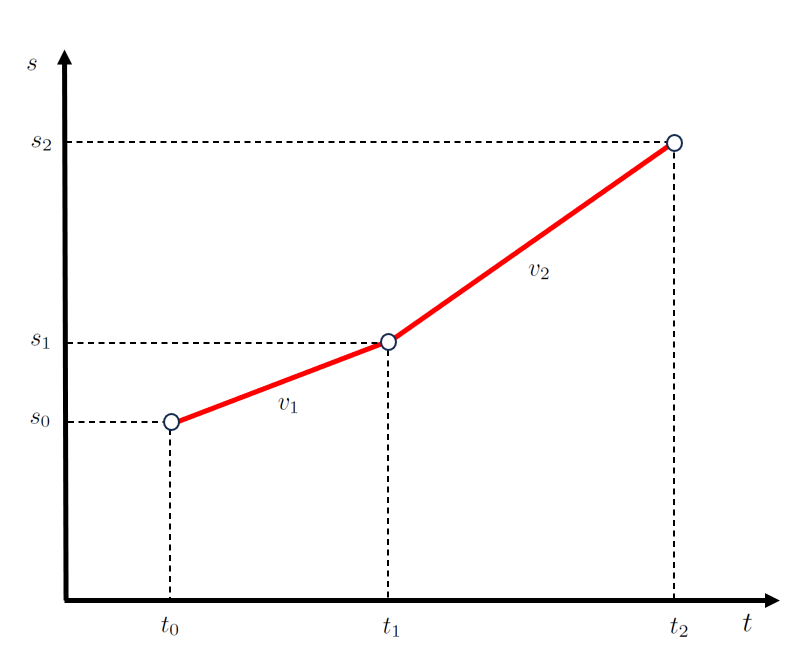
which is the key to the model represented by the network:
Mechanisms
ID:(15383, 0)
Two-stage concept
Top
In the case of a movement occurring in two stages, first, the object advances a distance of ($$) over a period of time of ($$) with a velocity of ($$).
Then, in a second stage, it advances a distance of ($$) over a period of time of ($$) with a velocity of ($$).
When represented graphically, we obtain a position-time diagram as follows:
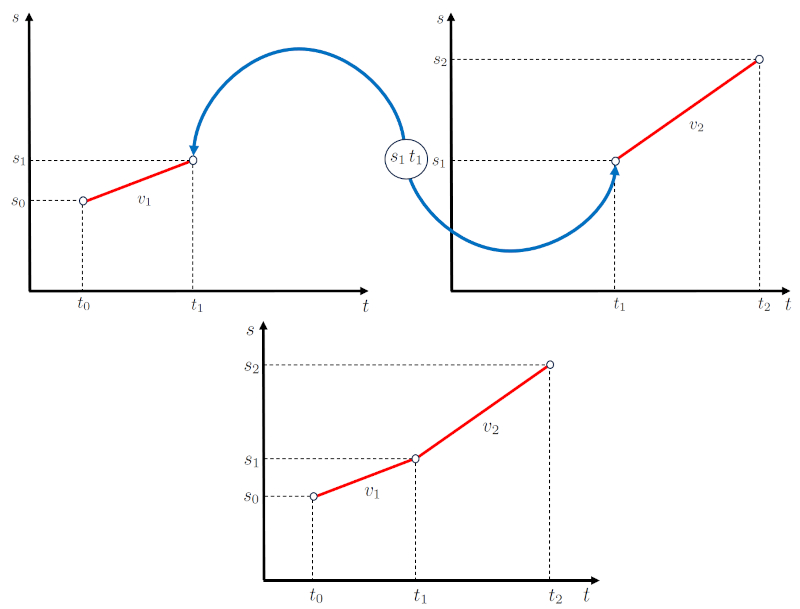
The key point to note is that the time spent in the first stage ($\Delta t_1$) and the time spent in the second stage ($\Delta t_2$) are sequential, just like the distance traveled in the first stage ($\Delta s_1$) and the distance traveled in the second stage ($\Delta s_2$).
ID:(15504, 0)
Speeds in two stages
Top
In the case of a movement occurring in two stages, first, the object advances a distance of ($$) over a period of time of ($$) with a velocity of ($$).
Then, in a second stage, it advances a distance of ($$) over a period of time of ($$) with a velocity of ($$).
When represented graphically, we obtain a position-time diagram as follows:
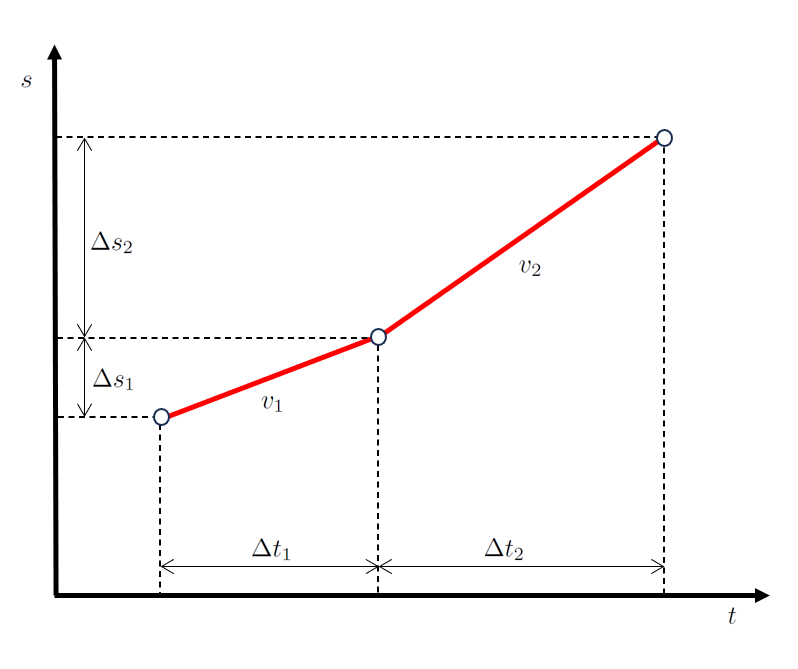
The key point to note is that the time spent in the first stage ($\Delta t_1$) and the time spent in the second stage ($\Delta t_2$) are sequential, just like the distance traveled in the first stage ($\Delta s_1$) and the distance traveled in the second stage ($\Delta s_2$).
ID:(15395, 0)
Positions and times in two stages
Top
In the case of a movement occurring in two stages, the first stage can be described by a function involving the points the start Time ($t_0$), the final time of first and start of second stage ($t_1$), the starting position ($s_0$), and the first final position and started second stage ($s_1$), represented by a line with a slope of the first stage speed ($v_1$):
| $ s_1 = s_0 + v_1 ( t_1 - t_0 )$ |
For the second stage, defined by the points the first final position and started second stage ($s_1$), the second stage final position ($s_2$), the final time of first and start of second stage ($t_1$), and the second stage ending time ($t_2$), a second line with a slope of the second stage speed ($v_2$) is employed:
| $ s_2 = s_1 + v_2 ( t_2 - t_1 )$ |
which is represented as:
It is important to note that the beginning of the second stage, defined by the points the final time of first and start of second stage ($t_1$) and the first final position and started second stage ($s_1$), coincides with the end of the first stage.
ID:(15396, 0)
Model
Top
The basic model involves two movements in consecutive stages.
In the first stage, it starts at the starting position ($s_0$) and ends at the first final position and started second stage ($s_1$), covering a distance of the distance traveled in the first stage ($\Delta s_1$), which starts at the start Time ($t_0$) and ends at the final time of first and start of second stage ($t_1$), lasting for the time spent in the first stage ($\Delta t_1$) with a velocity of the first stage speed ($v_1$).
In the second stage, it starts at the first final position and started second stage ($s_1$) and ends at the second stage final position ($s_2$), covering a distance of the distance traveled in the second stage ($\Delta s_2$), which starts at the final time of first and start of second stage ($t_1$) and ends at the second stage ending time ($t_2$), lasting for the distance traveled in the second stage ($\Delta s_2$) with a velocity of the second stage speed ($v_2$).
The resulting diagram consists of two sub-diagrams in which constant velocity is maintained. Both diagrams are connected by the first final position and started second stage ($s_1$) and the final time of first and start of second stage ($t_1$), which correspond to the endpoint of the first stage and the starting point of the second stage.
With this, the network structure of the model is as follows:
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \Delta s_1 \equiv s_1 - s_0 $
Ds = s - s_0
$ \Delta s_2 \equiv s_2 - s_1 $
Ds = s - s_0
$ \Delta t_1 \equiv t_1 - t_0 $
Dt = t - t_0
$ \Delta t_2 \equiv t_2 - t_1 $
Dt = t - t_0
$ s_1 = s_0 + v_1 ( t_1 - t_0 )$
s = s_0 + v_0 *( t - t_0 )
$ s_2 = s_1 + v_2 ( t_2 - t_1 )$
s = s_0 + v_0 *( t - t_0 )
$ v_1 \equiv\displaystyle\frac{ \Delta s_1 }{ \Delta t_1 }$
v_m = Ds / Dt
$ v_2 \equiv\displaystyle\frac{ \Delta s_2 }{ \Delta t_2 }$
v_m = Ds / Dt
ID:(15384, 0)
Distance traveled (1)
Equation
We can calculate the distance traveled in a time ($\Delta s$) from the starting position ($s_0$) and the position ($s$) using the following equation:
| $ \Delta s_1 \equiv s_1 - s_0 $ |
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 1)
Distance traveled (2)
Equation
We can calculate the distance traveled in a time ($\Delta s$) from the starting position ($s_0$) and the position ($s$) using the following equation:
| $ \Delta s_2 \equiv s_2 - s_1 $ |
| $ \Delta s \equiv s - s_0 $ |
ID:(4352, 2)
Elapsed time (1)
Equation
To describe the motion of an object, we need to calculate the time elapsed ($\Delta t$). This magnitude is obtained by measuring the start Time ($t_0$) and the the time ($t$) of said motion. The duration is determined by subtracting the initial time from the final time:
| $ \Delta t_1 \equiv t_1 - t_0 $ |
| $ \Delta t \equiv t - t_0 $ |
ID:(4353, 1)
Elapsed time (2)
Equation
To describe the motion of an object, we need to calculate the time elapsed ($\Delta t$). This magnitude is obtained by measuring the start Time ($t_0$) and the the time ($t$) of said motion. The duration is determined by subtracting the initial time from the final time:
| $ \Delta t_2 \equiv t_2 - t_1 $ |
| $ \Delta t \equiv t - t_0 $ |
ID:(4353, 2)
Average Speed (1)
Equation
The mean Speed ($\bar{v}$) can be calculated from the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$) using:
| $ v_1 \equiv\displaystyle\frac{ \Delta s_1 }{ \Delta t_1 }$ |
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(3152, 1)
Average Speed (2)
Equation
The mean Speed ($\bar{v}$) can be calculated from the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$) using:
| $ v_2 \equiv\displaystyle\frac{ \Delta s_2 }{ \Delta t_2 }$ |
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(3152, 2)
Case of Constant Speed (1)
Equation
If the speed is constant, the velocity will be equal to the initial Speed ($v_0$). In this case, the distance traveled as a function of time can be calculated using the difference between the position ($s$) and the starting position ($s_0$), divided by the difference between the time ($t$) and the start Time ($t_0$):
| $ s_1 = s_0 + v_1 ( t_1 - t_0 )$ |
| $ s = s_0 + v_0 ( t - t_0 )$ |
In the case where ($$) is equal to the mean Speed ($\bar{v}$):
| $ \bar{v} = v_0$ |
Therefore, with the distance traveled in a time ($\Delta s$) it is with the position ($s$) and the starting position ($s_0$):
| $ \Delta s \equiv s - s_0 $ |
and the time elapsed ($\Delta t$) is with the time ($t$) and the start Time ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
The equation for average velocity:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
can be written as:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
thus, solving for it we get:
| $ s = s_0 + v_0 ( t - t_0 )$ |
The corresponding equation defines a straight line in space-time.
ID:(3154, 1)
Case of Constant Speed (2)
Equation
If the speed is constant, the velocity will be equal to the initial Speed ($v_0$). In this case, the distance traveled as a function of time can be calculated using the difference between the position ($s$) and the starting position ($s_0$), divided by the difference between the time ($t$) and the start Time ($t_0$):
| $ s_2 = s_1 + v_2 ( t_2 - t_1 )$ |
| $ s = s_0 + v_0 ( t - t_0 )$ |
In the case where ($$) is equal to the mean Speed ($\bar{v}$):
| $ \bar{v} = v_0$ |
Therefore, with the distance traveled in a time ($\Delta s$) it is with the position ($s$) and the starting position ($s_0$):
| $ \Delta s \equiv s - s_0 $ |
and the time elapsed ($\Delta t$) is with the time ($t$) and the start Time ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
The equation for average velocity:
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
can be written as:
$v_0 = \bar{v} = \displaystyle\frac{\Delta s}{\Delta t} = \displaystyle\frac{s - s_0}{t - t_0}$
thus, solving for it we get:
| $ s = s_0 + v_0 ( t - t_0 )$ |
The corresponding equation defines a straight line in space-time.
ID:(3154, 2)