User:
Ballistic trajectory
Storyboard 
If an object is thrown or fired in a gravitational field, it undergoes two types of motion:
• In the vertical axis, it moves due to the gravitational field, experiencing gravitational acceleration. For low-height trajectories, this acceleration can be considered constant.
• In the horizontal axis, assuming air resistance is negligible, the object moves at a constant velocity because there is no force to accelerate or decelerate it.
The result is what is known as a ballistic trajectory, which achieves its maximum range when thrown or fired at a 45-degree angle.
ID:(1446, 0)
Vision in the Middle Ages
Concept
During the Middle Ages, when observing the flight of a cannonball, a curve was drawn that showed a steep ascent followed by an almost vertical drop, as seen in the image:
However, by analyzing the equations of kinematics, it is known that the actual trajectory of the cannonball is very different. In fact, it is a parabola that is produced by the combination of vertical motion caused by gravity and constant horizontal motion.
In other words, the time that the ball remains in the air is determined by its vertical motion, while the distance traveled in the horizontal direction is determined by its horizontal velocity.
ID:(13996, 0)
The ballistic trajectory
Concept
The ballistic trajectory typically follows an inverted parabola with a point of the maximum height reached ($y_{max}$) and ($$) with the maximum height time ($t_{max}$) and the time to impact ($t_{imp}$):
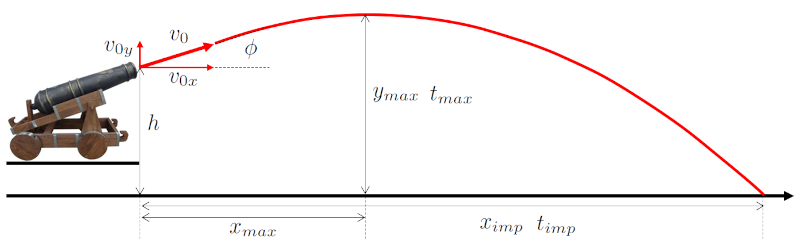
Note: Strictly speaking, the components should be estimated based on their values at ground level to accurately determine the parameters of the maximum height and impact point.
ID:(12536, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ t_{imp} =\displaystyle\frac{ v_0 \sin \phi }{ g }\left(1+\sqrt{1+\displaystyle\frac{ 2 g h }{ v_0 ^2 \sin^2 \phi }}\right)$
t_imp = v_0 *sin( phi )*(1+sqrt(1+2* g * h /(v_0 ^2*sin( phi )^2)))/ g
$ t_{max} =\displaystyle\frac{ v_0 }{ g }\sin \phi $
t_max = v_0 *sin( phi )/ g
$ v_{0x} = v_0 \cos \phi $
v_0x = v_0 *cos( phi )
$ v_{0y} = v_0 \sin \phi $
v_0y = v_0 *sin( phi )
$ x = v_{0x} t $
x = v_0x * t
$ x_{imp} =\displaystyle\frac{ v_0 ^2\sin \phi \cos \phi }{ g }\left(1 + \sqrt{1 + \displaystyle\frac{2 g h }{ v_0 ^2\sin^2 \phi }}\right) $
x_imp = v_0 ^2*sin( phi )*cos( phi )*(1+sqrt(1+2* g * h /( v_0 ^2*sin( phi )^2)))/ g
$ y = h + v_{0y} t -\displaystyle\frac{1}{2} g t ^2$
y = h + v_0y * t - g * t ^2/2
$ y_{max} = h + \displaystyle\frac{ v_0 ^2}{2 g }\sin^2 \phi $
y_max = h + v_0 ^2*sin( phi )^2/(2* g )
ID:(15407, 0)
Horizontal speed
Equation
If a point mass moves with ($$) and is fired downward ($$) with respect to the surface, then its the initial horizontal speed ($v_{0x}$) will be equal to:
| $ v_{0x} = v_0 \cos \phi $ |
ID:(10932, 0)
Vertical speed
Equation
If a point mass moves with ($$) and is fired downward ($$) with respect to the surface, then its the initial vertical speed ($v_{0y}$) will be equal to:
| $ v_{0y} = v_0 \sin \phi $ |
ID:(10933, 0)
Horizontal distance traveled
Equation
The object cycles through a time ($t$) to a initial horizontal speed ($v_{0x}$) A position on the x-axis ($x$) equal to
| $ x = v_{0x} t $ |
The position ($s$) traveled with the constant velocity ($v_0$) with the starting position ($s_0$), the time ($t$), and the start Time ($t_0$) is
| $ s = s_0 + v_0 ( t - t_0 )$ |
Therefore, if the motion starts at the origin ($s_0=0$) at the beginning of time ($t_0=0$), the motion is described by $x=s$ and $v_0=v_{0x}$.
| $ x = v_{0x} t $ |
ID:(10930, 0)
Vertical height reached
Equation
An object takes off in the terrestrial field with a velocity of the gravitational Acceleration ($g$), at an angle of ($$), and will reach ($$) at ($$).
| $ y = h + v_{0y} t -\displaystyle\frac{1}{2} g t ^2$ |
For the case where constant Acceleration ($a_0$) equals gravitational acceleration ($a_0=-g$), the vertical trajectory can be calculated using the equation for the position ($s$) with the starting position ($s_0$), the initial Speed ($v_0$), the time ($t$), and the start Time ($t_0$):
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
In the scenario where the motion starts at the height at which to shoot ($h$) ($s_0=h$), the start Time ($t_0$) ($t_0=0$), and the initial vertical speed ($v_{0y}$) ($v_0=v_{0y}$) are given, the motion can be described by the formula:
| $ y = h + v_{0y} t -\displaystyle\frac{1}{2} g t ^2$ |
Note: If you want the target to be at a higher point than the cannon, a negative ($$) should be used for the angle.
ID:(10931, 0)
Impact time
Equation
If an object moves with a velocity of a initial Speed ($v_0$) and is fired at an angle of a maximum height reached ($\phi$) relative to the surface, the time to impact ($t_{imp}$) can be calculated using the gravitational Acceleration ($g$) and the height at which to shoot ($h$):
| $ t_{imp} =\displaystyle\frac{ v_0 \sin \phi }{ g }\left(1+\sqrt{1+\displaystyle\frac{ 2 g h }{ v_0 ^2 \sin^2 \phi }}\right)$ |
To determine the impact time, we can use the equation of the position on the y-axis ($y$), which depends on the height at which to shoot ($h$), the initial vertical speed ($v_{0y}$), the gravitational Acceleration ($g$), and the time ($t$), where the height is zero:
| $ y = h + v_{0y} t -\displaystyle\frac{1}{2} g t ^2$ |
This results in a time:
$t=\displaystyle\frac{ v_{y0} +\sqrt{ v_{0y} ^2 + 2 g h }}{g}$
With the initial Speed ($v_0$) and the maximum height reached ($\phi$):
| $ v_{0y} = v_0 \sin \phi $ |
the time to impact ($t_{imp}$) is:
| $ t_{imp} =\displaystyle\frac{ v_0 \sin \phi }{ g }\left(1+\sqrt{1+\displaystyle\frac{ 2 g h }{ v_0 ^2 \sin^2 \phi }}\right)$ |
ID:(10934, 0)
Impact distance
Equation
If an object moves with a velocity of ($$) and is fired at an angle of ($$) relative to the surface, the gravitational Acceleration ($g$) and the height at which to shoot ($h$) can be calculated using the following formula:
| $ x_{imp} =\displaystyle\frac{ v_0 ^2\sin \phi \cos \phi }{ g }\left(1 + \sqrt{1 + \displaystyle\frac{2 g h }{ v_0 ^2\sin^2 \phi }}\right) $ |
Since the time to impact ($t_{imp}$) with the initial Speed ($v_0$), the maximum height reached ($\phi$), the gravitational Acceleration ($g$), and the height at which to shoot ($h$) is
| $ t_{imp} =\displaystyle\frac{ v_0 \sin \phi }{ g }\left(1+\sqrt{1+\displaystyle\frac{ 2 g h }{ v_0 ^2 \sin^2 \phi }}\right)$ |
then the position on the x-axis ($x$) with the initial horizontal speed ($v_{0x}$) and the time ($t$)
| $ x = v_{0x} t $ |
and the initial horizontal speed ($v_{0x}$) with the initial Speed ($v_0$) and the maximum height reached ($\phi$)
| $ v_{0x} = v_0 \cos \phi $ |
thus, we have
| $ x_{imp} =\displaystyle\frac{ v_0 ^2\sin \phi \cos \phi }{ g }\left(1 + \sqrt{1 + \displaystyle\frac{2 g h }{ v_0 ^2\sin^2 \phi }}\right) $ |
ID:(10935, 0)
Maximum height time
Equation
If an object moves with a velocity of the initial Speed ($v_0$) and is fired at an angle of ($$) with respect to the surface, the height at which it will reach its the maximum height reached ($y_{max}$) can be calculated as follows:
| $ t_{max} =\displaystyle\frac{ v_0 }{ g }\sin \phi $ |
The maximum height time ($t_{max}$) is reached when the position on the y-axis ($y$) reaches a maximum value. This height can be calculated with the height at which to shoot ($h$), the initial vertical speed ($v_{0y}$), the gravitational Acceleration ($g$), and the time ($t$),
| $ y = h + v_{0y} t -\displaystyle\frac{1}{2} g t ^2$ |
whose derivative with respect to time is zero at the maximum, implying:
$\displaystyle\frac{dy}{dt}=v_{0,y}-gt=0$
Therefore, with the expression for the initial Speed ($v_0$),
| $ v_{0y} = v_0 \sin \phi $ |
we have that
| $ t_{max} =\displaystyle\frac{ v_0 }{ g }\sin \phi $ |
ID:(10936, 0)
Maximum height
Equation
If the target is at a distance of the initial Speed ($v_0$) and is fired from an altitude of ($$) relative to the surface, with a velocity of the gravitational Acceleration ($g$), then the height it will reach, the maximum height reached ($y_{max}$), can be calculated as:
| $ y_{max} = h + \displaystyle\frac{ v_0 ^2}{2 g }\sin^2 \phi $ |
The maximum height reached ($y_{max}$) is reached in a maximum height time ($t_{max}$) with the maximum height reached ($\phi$), the constant velocity ($v_0$), and the gravitational Acceleration ($g$),
| $ t_{max} =\displaystyle\frac{ v_0 }{ g }\sin \phi $ |
from which we can determine the position on the y-axis ($y$) with the height at which to shoot ($h$), the initial vertical speed ($v_{0y}$), and the time ($t$) using the equation
| $ y = h + v_{0y} t -\displaystyle\frac{1}{2} g t ^2$ |
Thus, with the initial vertical speed ($v_{0y}$),
| $ v_{0y} = v_0 \sin \phi $ |
at the maximum height reached ($y_{max}$), it is
| $ y_{max} = h + \displaystyle\frac{ v_0 ^2}{2 g }\sin^2 \phi $ |
ID:(10937, 0)