Utilizador:
Mecanismos
Iframe 
O ciclo de Otto envolve quatro estágios principais: admissão, compressão, explosão e escape. Durante a fase de admissão, o motor aspira uma mistura de combustível e ar enquanto o pistão se move para baixo. A mistura é então comprimida à medida que o pistão se move para cima, o que aumenta a temperatura e a pressão do gás. No topo do curso de compressão, a vela de ignição acende a mistura comprimida, causando uma combustão rápida conhecida como o tempo de potência. Esta combustão empurra o pistão para baixo, fornecendo energia ao motor.
Após o tempo de potência, a válvula de escape se abre e o pistão se move para cima para expelir os gases de combustão do cilindro, completando o ciclo. O motor então repete esse ciclo continuamente durante a operação.
A eficiência de um motor que opera pelo ciclo de Otto depende do grau de compressão e das propriedades do combustível usado. Relações de compressão mais altas geralmente levam a uma melhor eficiência, mas requerem combustível de maior octanagem para evitar a detonação do motor. O ciclo de Otto é caracterizado por ser um ciclo de alta velocidade com cada estágio claramente definido, contribuindo significativamente para a eficiência geral e a produção de energia dos motores que o empregam.
Mecanismos
ID:(15282, 0)
Ciclo de Carnot
Conceito
Sadi Carnot introduziu [1] o conceito teórico do primeiro projeto de máquina capaz de gerar trabalho mecânico com base em um gradiente de temperatura. Isso é alcançado por meio de um processo no espaço pressão-volume, onde calor é adicionado e extraído, conforme ilustrado na imagem:
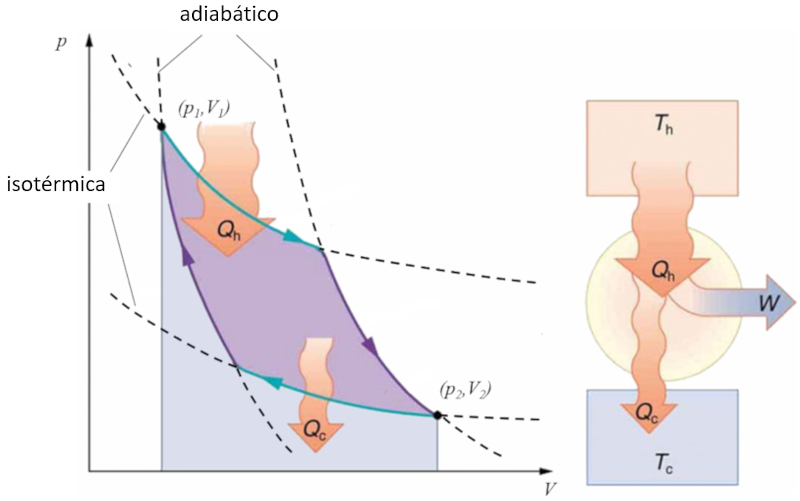
A área sob a curva o calor fornecido ($Q_H$), que se estende de 1 a 2, representa a energia necessária para transitar do estado ($p_1, V_1$) para o estado ($p_2, V_2$). Por outro lado, a área sob a curva o calor absorvido ($Q_C$), indo de 2 para 1, representa a extração de energia necessária para retornar do estado ($p_2, V_2$) ao estado ($p_1, V_1$). A diferença entre essas áreas corresponde à região delimitada por ambas as curvas e representa o trabalho eficaz ($W$) que o sistema pode realizar.
Carnot também demonstrou que, de acordo com a segunda lei da termodinâmica, o calor fornecido ($Q_H$) não pode ser igual a zero. Isso implica que não existem máquinas capazes de converter todo o calor em trabalho.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexões sobre a Potência Motriz do Fogo e sobre Máquinas Adequadas para Desenvolver Essa Potência), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Ciclo Otto: diagrama pressão-volume
Conceito
O ciclo de Otto [1] pode ser considerado uma solução técnica baseada no ciclo de Carnot. Nesse contexto, ele consiste em quatro estágios que são realizados da seguinte maneira:
• Estágio 1 para 2: Compressão adiabática $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_2)$,
• Estágio 2 para 3: Aquecimento $(p_2,V_2,T_2)\rightarrow(p_3,V_2,T_3)$,
• Estágio 3 para 4: Expansão adiabática $(p_3,V_2,T_3)\rightarrow(p_4,V_1,T_4)$,
• Estágio 4 para 1: Resfriamento $(p_4,V_1,T_4)\rightarrow(p_1,V_1,T_1)$
Esses estágios são ilustrados no seguinte diagrama:
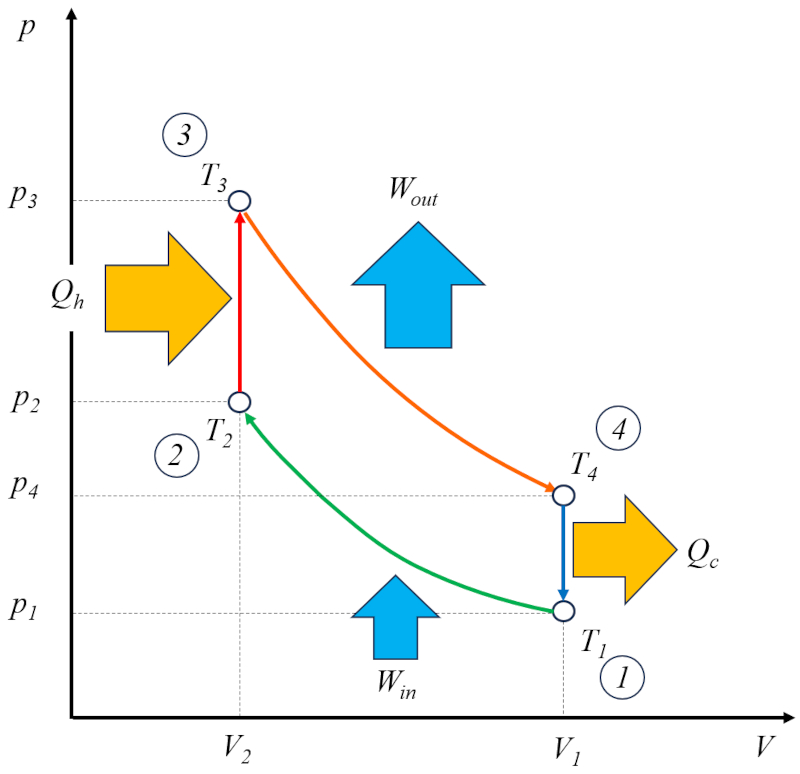
No diagrama, é ilustrado o fluxo de energia, onde o calor fornecido ($Q_H$) adiciona energia, elevando a temperatura de la temperatura no estado 2 ($T_2$) para la temperatura no estado 3 ($T_3$). Ele entra no sistema e realiza um trabalho eficaz ($W$) unidades de trabalho, enquanto o componente o calor absorvido ($Q_C$) é absorvido, diminuindo a temperatura de la temperatura no estado 4 ($T_4$) para la temperatura no estado 1 ($T_1$).
[1] "Verbrennungsmotor" (Motor de combustão interna), N. A. Otto, Kaiserlichen Patentamts, Patente 532, 2 de janeiro de 1877.
Nota: Em 1862, Nikolaus Otto tentou construir o motor de combustão interna patenteado por Alphonse Beau de Rochas sem sucesso. Mais tarde, ele o modificou e conseguiu construir um funcional em 1877, fabricando 30.000 motores silenciosos e altamente confiáveis. Ele patenteou seu projeto em 1877; no entanto, a patente foi posteriormente revogada devido à existência da patente de Alphonse Beau de Rochas, embora Rochas nunca tenha conseguido construir sua versão. Como Otto foi o primeiro a fazer o motor funcionar, sua versão é lembrada hoje, denominando o processo de "Ciclo de Otto".
ID:(11140, 0)
Elementos de uma geladeira
Conceito
O motor Otto opera em dois ciclos: o ciclo Otto propriamente dito, que consiste nas seguintes fases:
• Fase 1 para 2: Compressão adiabática
• Fase 2 para 3: Aquecimento
• Fase 3 para 4: Expansão adiabática
• Fase 4 para 1: Resfriamento
Além disso, ele possui um ciclo para esvaziar os gases queimados e preencher com uma nova mistura.
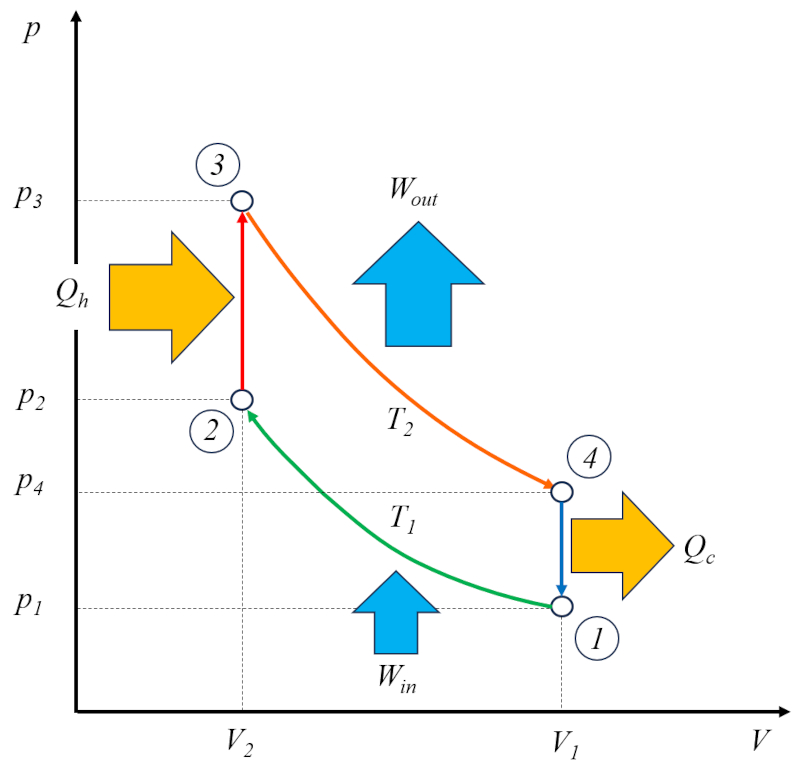
Por essa razão, ele é chamado de motor de dois tempos. A fase de esvaziamento e preenchimento pode ser realizada usando uma massa de compensação ou por meio de um segundo cilindro que opera fora de fase.
A eficiência la eficiência ($\eta$) do motor pode ser estimada usando o fator de compressibilidade Otto ($r$) e o índice adiabático ($\kappa$) com a seguinte equação:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(11142, 0)
Eficiência dependendo das temperaturas
Conceito
O calor absorvido ($Q_C$) está relacionado com la capacidade térmica em volume constante ($C_V$), la temperatura no estado 4 ($T_4$) e la temperatura no estado 1 ($T_1$) de acordo com a seguinte equação:
| $ Q_C = C_V ( T_4 - T_1 )$ |
E O calor fornecido ($Q_H$) está relacionado com la capacidade térmica em volume constante ($C_V$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 2 ($T_2$) através da equação:
| $ Q_H = C_V ( T_3 - T_2 )$ |
Portanto, na equação para la eficiência ($\eta$) representada por:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Temos a seguinte relação:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
ID:(15749, 0)
Eficiência em função do fator de compressibilidade
Conceito
La eficiência ($\eta$), em termos de la temperatura no estado 1 ($T_1$), la temperatura no estado 2 ($T_2$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 4 ($T_4$), é calculado usando a seguinte equação:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
No caso de expansão adiabática, ela é descrita usando o índice adiabático ($\kappa$), o volume expandido ($V_1$) e o volume compactado ($V_2$) com a relação:
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
E a compressão adiabática é representada pela relação:
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Se subtrairmos a segunda equação da primeira, obtemos:
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
O que nos leva à relação:
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Isso, por sua vez, leva à definição de o fator de compressibilidade Otto ($r$) com a seguinte equação:
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Com todos esses componentes, a eficiência de um processo usando o ciclo Otto pode ser calculada como:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(15750, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ c_V =\displaystyle\frac{ C_V }{ M }$
c_V = C_V / M
$ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$
eta = 1 - 1/ r ^( kappa -1)
$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$
eta =1-( T_4 - T_1 )/( T_3 - T_2 )
$ Q_C = C_V ( T_4 - T_1 )$
Q_C = C_V *( T_4 - T_1 )
$ Q_H = C_V ( T_3 - T_2 )$
Q_H = C_V *( T_3 - T_2 )
$ r =\displaystyle\frac{ V_1 }{ V_2 }$
r = V_1 / V_2
$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$
T_1 * V_1 ^( kappa -1)= T_2 V_2 ^( kappa - 1)
$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$
T_4 * V_1 ^( kappa -1)= T_3 V_2 ^( kappa - 1)
ID:(15341, 0)
Compressão adiabática
Equação
Neste caso, do ponto inicial 1 ao ponto 2. Isso significa que durante a compressão adiabática, o estado do gás muda de o volume expandido ($V_1$) e la temperatura no estado 1 ($T_1$) para o volume compactado ($V_2$) e la temperatura no estado 2 ($T_2$) da seguinte forma:
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Dado que em uma expansão adiabática, o gás satisfaz a relação com o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$) e la temperatura no estado final ($T_f$):
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Neste caso, do ponto inicial 1 ao ponto 2. Isso significa que durante a compressão adiabática, o estado do gás muda de o volume expandido ($V_1$) e la temperatura no estado 1 ($T_1$) para o volume compactado ($V_2$) e la temperatura no estado 2 ($T_2$) da seguinte forma:
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
ID:(11160, 0)
Calor fornecido
Equação
O calor fornecido ($Q_H$) pode ser calculado a partir de la capacidade térmica em volume constante ($C_V$), la temperatura no estado 2 ($T_2$) e la temperatura no estado 3 ($T_3$) usando a fórmula:
| $ Q_H = C_V ( T_3 - T_2 )$ |
Ao fornecer o calor fornecido ($Q_H$), a temperatura do gás aumenta de $T_2$ para $T_3$ em um processo isocórico (à volume constante). Isso implica que podemos utilizar a relação para ($$) com la capacidade térmica em volume constante ($C_V$) e ($$), expressa pela equação:
| $ dU = C_V \Delta T $ |
Isso resulta nos valores de la temperatura no estado 2 ($T_2$) e la temperatura no estado 3 ($T_3$) da seguinte forma:
| $ Q_H = C_V ( T_3 - T_2 )$ |
ID:(11157, 0)
Expansão adiabática
Equação
Neste caso, do ponto inicial 3 ao ponto 4. Isso significa que, durante a expansão adiabática, o estado do gás muda de o volume compactado ($V_2$) e la temperatura no estado 3 ($T_3$) para o volume expandido ($V_1$) e la temperatura no estado 4 ($T_4$), conforme:
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Durante uma expansão adiabática, o gás satisfaz a relação envolvendo o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$) e la temperatura no estado final ($T_f$):
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Neste caso, do ponto inicial 3 ao ponto 4. Isso significa que, durante a expansão adiabática, o estado do gás muda de o volume compactado ($V_2$) e la temperatura no estado 3 ($T_3$) para o volume expandido ($V_1$) e la temperatura no estado 4 ($T_4$), conforme:
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
.
ID:(11159, 0)
Calor removido
Equação
O calor absorvido ($Q_C$) pode ser calculado a partir de la capacidade térmica em volume constante ($C_V$), la temperatura no estado 4 ($T_4$) e la temperatura no estado 1 ($T_1$) usando a fórmula:
| $ Q_C = C_V ( T_4 - T_1 )$ |
Ao remover o calor absorvido ($Q_C$), a temperatura do gás aumenta de $T_1$ para $T_4$ em um processo isobárico (a pressão constante). Isso implica que podemos utilizar a relação para ($$) com la capacidade térmica em volume constante ($C_V$) e ($$), que é expressa pela equação:
| $ dU = C_V \Delta T $ |
Isso nos leva aos valores de la temperatura no estado 1 ($T_1$) e la temperatura no estado 4 ($T_4$) usando a fórmula:
| $ Q_C = C_V ( T_4 - T_1 )$ |
ID:(11145, 0)
Eficiência dependendo das temperaturas
Equação
La eficiência ($\eta$) é uma função de la temperatura no estado 1 ($T_1$), la temperatura no estado 2 ($T_2$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 4 ($T_4$) é igual a :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
O calor absorvido ($Q_C$) está relacionado com la capacidade térmica em volume constante ($C_V$), la temperatura no estado 4 ($T_4$) e la temperatura no estado 1 ($T_1$) de acordo com a seguinte equação:
| $ Q_C = C_V ( T_4 - T_1 )$ |
E O calor fornecido ($Q_H$) está relacionado com la capacidade térmica em volume constante ($C_V$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 2 ($T_2$) através da equação:
| $ Q_H = C_V ( T_3 - T_2 )$ |
Portanto, na equação para la eficiência ($\eta$) representada por:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Temos a seguinte relação:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
ID:(11161, 0)
Fator de compressão $r$
Equação
La eficiência ($\eta$) é, em última instância, uma função de o volume expandido ($V_1$) e o volume compactado ($V_2$), e em particular, de o fator de compressibilidade Otto ($r$):
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
A expansão adiabática é descrita usando as variáveis o índice adiabático ($\kappa$), la temperatura no estado 4 ($T_4$), la temperatura no estado 3 ($T_3$), o volume expandido ($V_1$) e o volume compactado ($V_2$) através da relação
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Enquanto a compressão adiabática é representada por la temperatura no estado 1 ($T_1$) e la temperatura no estado 2 ($T_2$) através da relação
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Subtraindo a segunda equação da primeira, obtemos
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
O que nos leva à relação
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
E isso nos permite definir o fator de compressibilidade Otto ($r$) da seguinte forma:
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
ID:(11162, 0)
Eficiência em função do fator de compressibilidade
Equação
La eficiência ($\eta$) pode ser calculado a partir de o fator de compressibilidade Otto ($r$) e o índice adiabático ($\kappa$) no caso do ciclo Otto usando:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
La eficiência ($\eta$), em termos de la temperatura no estado 1 ($T_1$), la temperatura no estado 2 ($T_2$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 4 ($T_4$), é calculado usando a seguinte equação:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
No caso de expansão adiabática, ela é descrita usando o índice adiabático ($\kappa$), o volume expandido ($V_1$) e o volume compactado ($V_2$) com a relação:
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
E a compressão adiabática é representada pela relação:
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Se subtrairmos a segunda equação da primeira, obtemos:
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
O que nos leva à relação:
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Isso, por sua vez, leva à definição de o fator de compressibilidade Otto ($r$) com a seguinte equação:
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Com todos esses componentes, a eficiência de um processo usando o ciclo Otto pode ser calculada como:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
.
ID:(11163, 0)
Calor específico dos gases a volume constante
Equação
O calor específico dos gases a volume constante ($c_V$) é igual a la capacidade térmica em volume constante ($C_V$) dividido por la massa ($M$):
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
Seguindo uma analogia ao calor específico ($c$) para líquidos e sólidos com la capacidade calórica ($C$) e la massa ($M$):
| $ c =\displaystyle\frac{ C }{ M }$ |
existe também um calor específico dos gases a volume constante ($c_V$) para aquecimento a volume constante com la capacidade térmica em volume constante ($C_V$):
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
ID:(11113, 0)