Storyboard

>Modelo

ID:(1487, 0)

Iframe

>Top

O ciclo Diesel é um ciclo termodinâmico que fundamenta o funcionamento dos motores diesel, amplamente utilizados em veículos e maquinaria industrial. Desenvolvido por Rudolf Diesel na década de 1890, este ciclo distingue-se principalmente pelo seu processo de ignição em comparação com o ciclo Otto dos motores a gasolina. No ciclo Diesel, o ar é aspirado para o cilindro e comprimido a uma taxa muito mais alta do que nos motores a gasolina, o que eleva sua temperatura a um ponto que pode inflamar o combustível diesel sem a necessidade de uma vela de ignição.

Durante a operação, o ciclo começa com o pistão puxando ar enquanto se move para baixo. Em seguida, o ar é comprimido no movimento ascendente, aumentando sua temperatura. No pico da fase de compressão, o combustível é injetado no ar comprimido e quente em forma de uma fina névoa, causando ignição espontânea. A combustão empurra o pistão para baixo, gerando energia. Por fim, na fase de exaustão, os gases resultantes da combustão são expelidos quando o pistão se move para cima novamente, completando o ciclo.

Os motores Diesel são conhecidos por sua eficiência e durabilidade. A alta taxa de compressão não só permite que o motor extraia mais energia do combustível, mas também aumenta sua eficiência térmica, o que significa que uma maior parte da energia do combustível é convertida em trabalho mecânico. Os motores Diesel geralmente oferecem uma melhor eficiência de combustível e produzem menos emissões de CO2 por unidade de energia em comparação com seus equivalentes a gasolina, mas podem emitir níveis mais altos de outros poluentes, como óxidos de nitrogênio e partículas.

ID:(15283, 0)

Conceito

>Top

Sadi Carnot introduziu [1] o conceito teórico do primeiro projeto de máquina capaz de gerar trabalho mecânico com base em um gradiente de temperatura. Isso é alcançado por meio de um processo no espaço pressão-volume, onde calor é adicionado e extraído, conforme ilustrado na imagem:

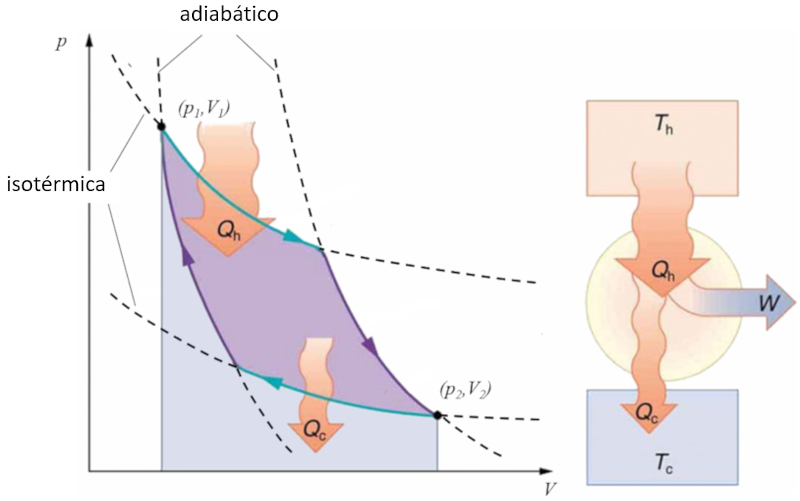
A área sob a curva o calor fornecido ($Q_H$), que se estende de 1 a 2, representa a energia necessária para transitar do estado ($p_1, V_1$) para o estado ($p_2, V_2$). Por outro lado, a área sob a curva o calor absorvido ($Q_C$), indo de 2 para 1, representa a extração de energia necessária para retornar do estado ($p_2, V_2$) ao estado ($p_1, V_1$). A diferença entre essas áreas corresponde à região delimitada por ambas as curvas e representa o trabalho eficaz ($W$) que o sistema pode realizar.

Carnot também demonstrou que, de acordo com a segunda lei da termodinâmica, o calor fornecido ($Q_H$) não pode ser igual a zero. Isso implica que não existem máquinas capazes de converter todo o calor em trabalho.

[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexões sobre a Potência Motriz do Fogo e sobre Máquinas Adequadas para Desenvolver Essa Potência), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)

ID:(11131, 0)

Conceito

>Top

Rudolf Diesel [1] propôs criar um ciclo distinto do ciclo de Carnot com o objetivo de alcançar uma eficiência superior em comparação com o ciclo de Otto. Esse processo se desenrola nas seguintes etapas:

• Estágio 1 a 2: Compressão adiabática $(p_1,V_1,T_1)\rightarrow (p_2,V_2,T_2)$,
• Estágio 2 a 3: Aquecimento e expansão à pressão constante $(p_2,V_2,T_2)\rightarrow (p_2,V_3,T_3)$,
• Estágio 3 a 4: Expansão adiabática $(p_2,V_3,T_3)\rightarrow (p_3,V_1,T_4)$,
• Estágio 4 a 1: Resfriamento a volume constante $(p_3,V_1,T_4)\rightarrow (p_1,V_1,T_1)$

Esses estágios são ilustrados abaixo:

A chave está no estágio 2 a 3, onde a expansão ocorre à pressão constante. A razão torna-se evidente ao examinarmos o gráfico:

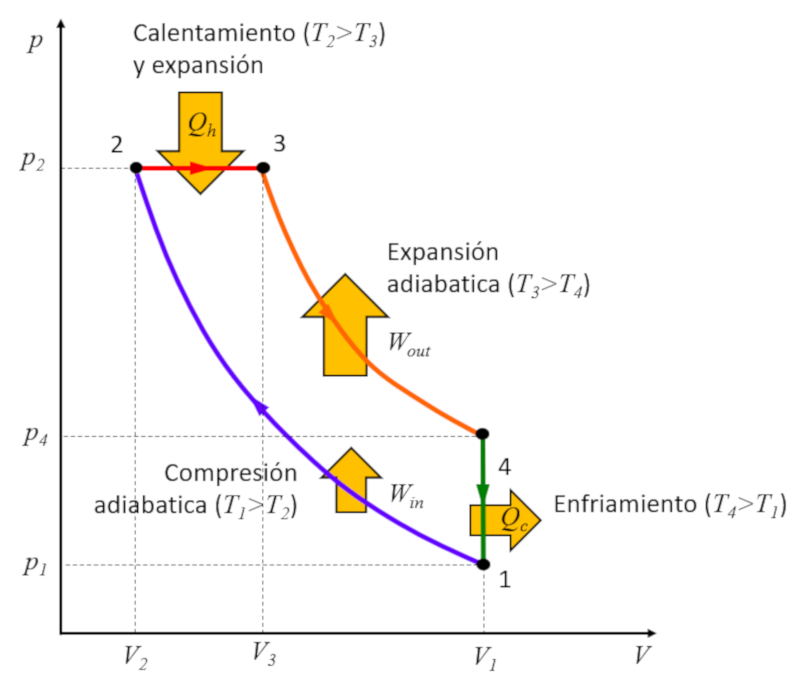
A energia ganha é igual à área contida dentro do ciclo, e ao realizar a compressão à pressão constante, essa área é maior do que no caso da compressão a volume constante.

[1] "Verfahren zur Entwickelung eines rationellen Wärmemotors zum Ersatz der Dampfmaschine und der heute bekannten Verbrennungsmotoren" (Método para o Desenvolvimento de um Motor Térmico Racional para Substituir a Máquina a Vapor e os Motores de Combustão Contemporâneos), Rudolf Diesel, Kaiserlichen Patentamts, No. 67207 (1892)

ID:(11141, 0)

Conceito

>Top

Tanto o ciclo Otto quanto o ciclo Diesel dependem das variáveis la temperatura no estado 1 ($T_1$), la temperatura no estado 2 ($T_2$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 4 ($T_4$). No entanto, no caso do ciclo Diesel, ele também depende de o índice adiabático ($\kappa$), cujo valor é 1,4.

No ciclo Otto, a eficiência é calculada com base na temperatura usando a seguinte equação:

Já no ciclo Diesel, a eficiência é calculada com base na temperatura usando a seguinte equação:

A inclusão do fator $1/\kappa \sim 0,71$ no ciclo Diesel o torna mais eficiente em comparação com o ciclo Otto para a mesma configuração de temperatura. Isso é resultado direto do aumento da área contida na curva que representa o ciclo na representação pressão-volume.

ID:(11153, 0)

Conceito

>Top

Dado que em uma expansão adiabática, o gás atende às relações o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$) e o índice adiabático ($\kappa$) expressas como:

Podemos observar que na mudança de estado de o volume intermediário ($V_3$) e la temperatura no estado 3 ($T_3$) para o volume expandido ($V_1$) e la temperatura no estado 4 ($T_4$), a seguinte igualdade se mantém:

$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$

Usando a equação para o fator de expansibilidade ($r_E$):

Obtemos:

ID:(15751, 0)

Conceito

>Top

Dado que em uma expansão adiabática, o gás satisfaz as relações o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$) e o índice adiabático ($\kappa$), expressas como:

Podemos observar que durante a mudança de estado de o volume expandido ($V_1$) e la temperatura no estado 1 ($T_1$) para o volume compactado ($V_2$) e la temperatura no estado 2 ($T_2$), a seguinte igualdade é mantida:

$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$

Usando a equação para o facteur de compressibilité ($r_C$):

Obtemos:

ID:(15752, 0)

Conceito

>Top

Como o aquecimento ocorre a pressão constante, aplicamos a lei de Charles:

Portanto, a mudança de estado ($V_2, T_2$) para ($V_3, T_3$) deve satisfazer a equação:

$\displaystyle\frac{T_2}{V_2} = \displaystyle\frac{T_3}{V_3}$

Com as equações:

podemos reescrever como:

$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$

ou seja:

ID:(15753, 0)

Conceito

>Top

A eficiência em relação à temperatura é definida por:

com as quantidades de calor fornecido:

e absorvido:

temos a relação de eficiência em função da temperatura:

ID:(15754, 0)

Conceito

>Top

O valor de la eficiência ($\eta$) pode ser calculado usando os valores o índice adiabático ($\kappa$), la temperatura no estado 1 ($T_1$), la temperatura no estado 2 ($T_2$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 4 ($T_4$) na seguinte equação:

Além disso, as relações entre as temperaturas com o facteur de compressibilité ($r_C$) e o fator de expansibilidade ($r_E$) são definidas pelas seguintes equações:

Adicionalmente, o valor de o índice adiabático ($\kappa$) é utilizado na equação:

Essas equações nos permitem calcular o desempenho de um processo que segue o ciclo Diesel usando a seguinte equação:

ID:(15755, 0)

Top

>Top

Parâmetros

$c_V$

c_V

Calor específico dos gases a volume constante

J/kg K

$C_p$

C_p

Capacidade térmica a pressão constante

J/kg

$C_V$

C_V

Capacidade térmica em volume constante

J/kg

$r_C$

r_C

Facteur de compressibilité

-

$r_E$

r_E

Fator de expansibilidade

-

$\kappa$

kappa

Índice adiabático

-

$M$

M

Massa

kg

Variáveis

$Q_C$

Q_C

Calor absorvido

J

$Q_H$

Q_H

Calor fornecido

J

$\eta$

eta

Eficiência

-

$T_1$

T_1

Temperatura no estado 1

K

$T_2$

T_2

Temperatura no estado 2

K

$T_3$

T_3

Temperatura no estado 3

K

$T_4$

T_4

Temperatura no estado 4

K

$V_2$

V_2

Volume compactado

m^3

$V_1$

V_1

Volume expandido

m^3

$V_3$

V_3

Volume intermediário

m^3

Cálculos

• Método alternativo
• Método tradicional
• Estratégia
• 2D
• 3D

Equação

Equação

Primeiro, selecione a equação: para , depois, selecione a variável: para

---

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve Dado Calcular Objetivo : Equação A ser usado

Equações

ID:(15342, 0)

Equação

>Top, >Modelo

Neste caso, do ponto inicial 1 ao ponto 2. Isso significa que durante a compressão adiabática, o estado do gás muda de o volume expandido ($V_1$) e la temperatura no estado 1 ($T_1$) para o volume compactado ($V_2$) e la temperatura no estado 2 ($T_2$) da seguinte forma:

$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$

Condições

Variáveis

$\kappa$

Índice adiabático

$-$

6661

$T_1$

Temperatura no estado 1

$K$

8489

$T_2$

Temperatura no estado 2

$K$

8490

$V_2$

Volume compactado

$m^3$

8498

$V_1$

Volume expandido

$m^3$

8497

Relação

Desenvolvimento

Dado que em uma expansão adiabática, o gás satisfaz a relação com o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$) e la temperatura no estado final ($T_f$):

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$

Neste caso, do ponto inicial 1 ao ponto 2. Isso significa que durante a compressão adiabática, o estado do gás muda de o volume expandido ($V_1$) e la temperatura no estado 1 ($T_1$) para o volume compactado ($V_2$) e la temperatura no estado 2 ($T_2$) da seguinte forma:

$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$

ID:(11160, 0)

Equação

>Top, >Modelo

O calor fornecido ($Q_H$) pode ser calculado com la capacidade térmica a pressão constante ($C_p$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 2 ($T_2$) usando a fórmula:

$ Q_H = C_p ( T_3 - T_2 )$

Condições

Variáveis

$Q_H$

Calor fornecido

$J$

8170

$C_p$

Capacidade térmica a pressão constante

$J/K$

7937

$T_2$

Temperatura no estado 2

$K$

8490

$T_3$

Temperatura no estado 3

$K$

8491

Relação

Desenvolvimento

Ao fornecer o calor fornecido ($Q_H$), a temperatura do gás aumenta de $T_2$ para $T_3$ em um processo isobárico (à pressão constante). Isso implica que podemos utilizar a relação para ($$) com la capacidade térmica a pressão constante ($C_p$) e ($$), expressa pela equação:

$ \Delta Q = C_p \Delta T $

Isso nos leva aos valores de la temperatura no estado 3 ($T_3$) e la temperatura no estado 2 ($T_2$) usando a fórmula:

$ Q_H = C_p ( T_3 - T_2 )$

ID:(11144, 0)

Equação

>Top, >Modelo

Neste caso, do ponto inicial 3 ao ponto 4. Isso significa que, durante a expansão adiabática, o estado do gás muda de o volume compactado ($V_2$) e la temperatura no estado 3 ($T_3$) para o volume expandido ($V_1$) e la temperatura no estado 4 ($T_4$), conforme:

$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$

Condições

Variáveis

$\kappa$

Índice adiabático

$-$

6661

$T_3$

Temperatura no estado 3

$K$

8491

$T_4$

Temperatura no estado 4

$K$

8492

$V_2$

Volume compactado

$m^3$

8498

$V_1$

Volume expandido

$m^3$

8497

Relação

Desenvolvimento

Durante uma expansão adiabática, o gás satisfaz a relação envolvendo o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$) e la temperatura no estado final ($T_f$):

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$

Neste caso, do ponto inicial 3 ao ponto 4. Isso significa que, durante a expansão adiabática, o estado do gás muda de o volume compactado ($V_2$) e la temperatura no estado 3 ($T_3$) para o volume expandido ($V_1$) e la temperatura no estado 4 ($T_4$), conforme:

$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$

.

ID:(11159, 0)

Equação

>Top, >Modelo

O calor absorvido ($Q_C$) pode ser calculado a partir de la capacidade térmica em volume constante ($C_V$), la temperatura no estado 4 ($T_4$) e la temperatura no estado 1 ($T_1$) usando a fórmula:

$ Q_C = C_V ( T_4 - T_1 )$

Condições

Variáveis

$Q_C$

Calor absorvido

$J$

8171

$C_V$

Capacidade térmica em volume constante

$J/K$

8481

$T_1$

Temperatura no estado 1

$K$

8489

$T_4$

Temperatura no estado 4

$K$

8492

Relação

Desenvolvimento

Ao remover o calor absorvido ($Q_C$), a temperatura do gás aumenta de $T_1$ para $T_4$ em um processo isobárico (a pressão constante). Isso implica que podemos utilizar a relação para ($$) com la capacidade térmica em volume constante ($C_V$) e ($$), que é expressa pela equação:

$ dU = C_V \Delta T $

Isso nos leva aos valores de la temperatura no estado 1 ($T_1$) e la temperatura no estado 4 ($T_4$) usando a fórmula:

$ Q_C = C_V ( T_4 - T_1 )$

ID:(11145, 0)

Equação

>Top, >Modelo

Na análise do ciclo Diesel, é útil introduzir o chamado o facteur de compressibilité ($r_C$), que representa a relação entre o volume expandido ($V_1$) e o volume compactado ($V_2$) durante a compressão da mistura, conforme mostrado na seguinte expressão:

$ r_C =\displaystyle\frac{ V_1 }{ V_2 }$

Condições

Variáveis

$r_C$

Facteur de compressibilité

$-$

8501

$V_2$

Volume compactado

$m^3$

8498

$V_1$

Volume expandido

$m^3$

8497

Relação

ID:(11146, 0)

Equação

>Top, >Modelo

Na análise do ciclo Diesel, é vantajoso introduzir o termo o fator de expansibilidade ($r_E$), que representa a relação entre o volume expandido ($V_1$) e o volume intermediário ($V_3$) durante a compressão da mistura, conforme ilustrado na seguinte expressão:

$ r_E =\displaystyle\frac{ V_1 }{ V_3 }$

Condições

Variáveis

$r_E$

Fator de expansibilidade

$-$

8502

$V_1$

Volume expandido

$m^3$

8497

$V_3$

Volume intermediário

$m^3$

8499

Relação

ID:(11147, 0)

Equação

>Top, >Modelo

La temperatura no estado 3 ($T_3$) pode ser calculado com la temperatura no estado 4 ($T_4$), o fator de expansibilidade ($r_E$) e o índice adiabático ($\kappa$) usando:

$ T_3 = T_4 r_E ^{ \kappa - 1}$

Condições

Variáveis

$r_E$

Fator de expansibilidade

$-$

8502

$\kappa$

Índice adiabático

$-$

6661

$T_3$

Temperatura no estado 3

$K$

8491

$T_4$

Temperatura no estado 4

$K$

8492

Relação

Desenvolvimento

Dado que em uma expansão adiabática, o gás atende às relações o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$) e o índice adiabático ($\kappa$) expressas como:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$

Podemos observar que na mudança de estado de o volume intermediário ($V_3$) e la temperatura no estado 3 ($T_3$) para o volume expandido ($V_1$) e la temperatura no estado 4 ($T_4$), a seguinte igualdade se mantém:

$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$

Usando a equação para o fator de expansibilidade ($r_E$):

$ r_E =\displaystyle\frac{ V_1 }{ V_3 }$

Obtemos:

$ T_3 = T_4 r_E ^{ \kappa - 1}$

ID:(11149, 0)

Equação

>Top, >Modelo

La temperatura no estado 2 ($T_2$) pode ser calculado a partir de la temperatura no estado 1 ($T_1$), o facteur de compressibilité ($r_C$) e o índice adiabático ($\kappa$) usando:

$ T_2 = T_1 r_C ^{ \kappa - 1}$

Condições

Variáveis

$r_C$

Facteur de compressibilité

$-$

8501

$\kappa$

Índice adiabático

$-$

6661

$T_1$

Temperatura no estado 1

$K$

8489

$T_2$

Temperatura no estado 2

$K$

8490

Relação

Desenvolvimento

Dado que em uma expansão adiabática, o gás satisfaz as relações o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$) e o índice adiabático ($\kappa$), expressas como:

$ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$

Podemos observar que durante a mudança de estado de o volume expandido ($V_1$) e la temperatura no estado 1 ($T_1$) para o volume compactado ($V_2$) e la temperatura no estado 2 ($T_2$), a seguinte igualdade é mantida:

$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$

Usando a equação para o facteur de compressibilité ($r_C$):

$ r_C =\displaystyle\frac{ V_1 }{ V_2 }$

Obtemos:

$ T_2 = T_1 r_C ^{ \kappa - 1}$

ID:(11148, 0)

Equação

>Top, >Modelo

La temperatura no estado 3 ($T_3$) pode ser calculado a partir de la temperatura no estado 2 ($T_2$), o facteur de compressibilité ($r_C$) e o fator de expansibilidade ($r_E$) usando:

$ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $

Condições

Variáveis

$r_C$

Facteur de compressibilité

$-$

8501

$r_E$

Fator de expansibilidade

$-$

8502

$T_2$

Temperatura no estado 2

$K$

8490

$T_3$

Temperatura no estado 3

$K$

8491

Relação

Desenvolvimento

Como o aquecimento ocorre a pressão constante, aplicamos a lei de Charles:

$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$

Portanto, a mudança de estado ($V_2, T_2$) para ($V_3, T_3$) deve satisfazer a equação:

$\displaystyle\frac{T_2}{V_2} = \displaystyle\frac{T_3}{V_3}$

Com as equações:

$ r_C =\displaystyle\frac{ V_1 }{ V_2 }$

$ r_E =\displaystyle\frac{ V_1 }{ V_3 }$

podemos reescrever como:

$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$

ou seja:

$ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $

ID:(11150, 0)

Equação

>Top, >Modelo

La eficiência ($\eta$) pode ser calculado a partir de o índice adiabático ($\kappa$), la temperatura no estado 1 ($T_1$), la temperatura no estado 2 ($T_2$), la temperatura no estado 3 ($T_3$) e 8492 usando:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

Condições

Variáveis

$\eta$

Eficiência

$-$

5245

$\kappa$

Índice adiabático

$-$

6661

$T_1$

Temperatura no estado 1

$K$

8489

$T_2$

Temperatura no estado 2

$K$

8490

$T_3$

Temperatura no estado 3

$K$

8491

$T_4$

Temperatura no estado 4

$K$

8492

Relação

Desenvolvimento

A eficiência em relação à temperatura é definida por:

$ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $

com as quantidades de calor fornecido:

$ Q_H = C_p ( T_3 - T_2 )$

e absorvido:

$ Q_C = C_V ( T_4 - T_1 )$

temos a relação de eficiência em função da temperatura:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

ID:(11164, 0)

Equação

>Top, >Modelo

O cálculo de la eficiência ($\eta$) é realizado usando o índice adiabático ($\kappa$), o facteur de compressibilité ($r_C$) e o fator de expansibilidade ($r_E$), como segue:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ r_E ^{- \kappa }- r_C ^{- \kappa }}{ r_E ^{-1}- r_C ^{-1}}$

Condições

Variáveis

$\eta$

Eficiência

$-$

5245

$r_C$

Facteur de compressibilité

$-$

8501

$r_E$

Fator de expansibilidade

$-$

8502

$\kappa$

Índice adiabático

$-$

6661

Relação

Desenvolvimento

O valor de la eficiência ($\eta$) pode ser calculado usando os valores o índice adiabático ($\kappa$), la temperatura no estado 1 ($T_1$), la temperatura no estado 2 ($T_2$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 4 ($T_4$) na seguinte equação:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$

Além disso, as relações entre as temperaturas com o facteur de compressibilité ($r_C$) e o fator de expansibilidade ($r_E$) são definidas pelas seguintes equações:

$ T_2 = T_1 r_C ^{ \kappa - 1}$

$ T_3 = T_4 r_E ^{ \kappa - 1}$

$ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $

Adicionalmente, o valor de o índice adiabático ($\kappa$) é utilizado na equação:

$ \kappa =\displaystyle\frac{ C_p }{ C_V }$

Essas equações nos permitem calcular o desempenho de um processo que segue o ciclo Diesel usando a seguinte equação:

$ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ r_E ^{- \kappa }- r_C ^{- \kappa }}{ r_E ^{-1}- r_C ^{-1}}$

ID:(11156, 0)

Equação

>Top, >Modelo

($$) é igual a la capacidade térmica a pressão constante ($C_p$) dividido por la massa ($M$):

$ c_p =\displaystyle\frac{ C_p }{ M }$

Condições

Variáveis

$C_p$

Capacidade térmica a pressão constante

$J/K$

7937

$M$

Massa

$kg$

5215

Relação

Desenvolvimento

Seguindo uma analogia ao calor específico ($c$) para líquidos e sólidos com la capacidade calórica ($C$) e la massa ($M$):

$ c =\displaystyle\frac{ C }{ M }$

existe também ($$) para o aquecimento a pressão constante com la capacidade térmica a pressão constante ($C_p$):

$ c_p =\displaystyle\frac{ C_p }{ M }$

ID:(11114, 0)

Equação

>Top, >Modelo

O calor específico dos gases a volume constante ($c_V$) é igual a la capacidade térmica em volume constante ($C_V$) dividido por la massa ($M$):

$ c_V =\displaystyle\frac{ C_V }{ M }$

Condições

Variáveis

$c_V$

Calor específico dos gases a volume constante

$J/kg K$

6662

$C_V$

Capacidade térmica em volume constante

$J/K$

8481

$M$

Massa

$kg$

5215

Relação

Desenvolvimento

Seguindo uma analogia ao calor específico ($c$) para líquidos e sólidos com la capacidade calórica ($C$) e la massa ($M$):

$ c =\displaystyle\frac{ C }{ M }$

existe também um calor específico dos gases a volume constante ($c_V$) para aquecimento a volume constante com la capacidade térmica em volume constante ($C_V$):

$ c_V =\displaystyle\frac{ C_V }{ M }$

ID:(11113, 0)