User:
The Stirling Cycle
Storyboard 
A thermodynamic machine that doesn't rely on internal combustion but instead receives heat input externally. This process still generates the typical pressure-volume cycle, allowing for modeling and calculating the achieved efficiency.
ID:(1485, 0)
Mechanisms
Iframe
The Stirling cycle involves four main phases: heating, expansion, cooling, and compression, conducted in a sealed environment where a gas such as helium or hydrogen serves as the working fluid.
During the heating phase, the gas is heated at constant volume, absorbing heat from an external source which increases its temperature and pressure. This is followed by the expansion phase, where the heated gas expands and does work on a piston or other mechanism, dropping in temperature and pressure but converting the heat into mechanical energy.
The cooling phase then occurs at constant volume. Here, the gas loses heat, which decreases its temperature and pressure, preparing it for the final phase. The regenerator plays a critical role by absorbing heat from the gas, which conserves energy and enhances efficiency.
The cycle concludes with the compression of the cooled gas, which requires less energy than what was produced during expansion. This compression increases the gass temperature, though not as much as during the initial heating phase, and the cycle begins anew.
The regenerator is vital throughout this process, storing heat from the cooling phase and returning it during heating, thereby reusing energy within the system and significantly boosting the engines thermal efficiency. Stirling engines are valued for their quiet operation and the flexibility to use any heat source, making them adaptable and environmentally beneficial for various applications.
Mechanisms
ID:(15284, 0)
Carnot cycle
Concept
Sadi Carnot introduced [1] the theoretical concept of the first machine design capable of generating mechanical work based on a heat gradient. This concept is realized through a process in the pressure-volume space where heat is added and extracted, as depicted in the image:
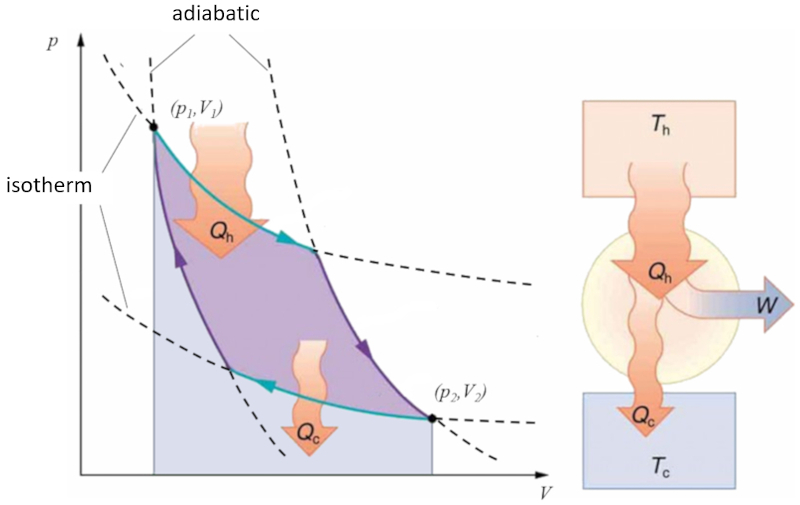
The area under curve the heat supplied ($Q_H$), spanning from 1 to 2, represents the energy input required to transition from state ($p_1, V_1$) to state ($p_2, V_2$). Conversely, the area under curve the absorbed heat ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from state ($p_2, V_2$) back to state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents the effective work ($W$) that the system can perform.
Carnot also demonstrated that, in accordance with the second law of thermodynamics, the heat supplied ($Q_H$) cannot equal zero. This implies that no machine can convert all heat into work.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflections on the Motive Power of Fire and on Machines Fitted to Develop That Power), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Stirling cycle: Pressure-volume diagram
Top
The Stirling cycle [1] can be considered as a technical solution based on the Carnot cycle, which consists of four well-defined stages:
Stage 1 to 2: Isothermal compression $(p_1, V_1, T_1) \rightarrow (p_2, V_2, T_1)$.
Stage 2 to 3: Isochoric heating $(p_2, V_2, T_1) \rightarrow (p_3, V_2, T_2)$.
Stage 3 to 4: Isothermal expansion $(p_3, V_2, T_2) \rightarrow (p_4, V_1, T_2)$.
Stage 4 to 1: Isochoric cooling $(p_4, V_1, T_2) \rightarrow (p_1, V_1, T_1)$.
It is important to note that this cycle does not involve an adiabatic phase; instead, it relies on the exchange between isochoric processes (at constant volume) and isothermal processes (at constant temperature).
These stages can be visualized in the following diagram:
[1] "An Economical Engine for the Purpose of Pumping Water by the Expansive Force of Steam," Robert Stirling, British Patent No. 4081 of 1816.
ID:(15362, 0)
Stirling cycle 1 to 2
Concept
In the first stage the number of moles ($n$) the gas is compressed with the work done on the system ($W_{in}$) from the expanded volume ($V_1$) to the compressed volume ($V_2$) isothermally to the temperature in state 1 ($T_1$):
The work is calculated using the integral of the work done on the system ($W_{in}$) with the number of moles ($n$) and the pressure ($p$), integrated in the volume ($V$), from the expanded volume ($V_1$) to the compressed volume ($V_2$):
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
If the pressure ($p$) is obtained using the universal gas constant ($R$), the number of moles ($n$), and the absolute temperature ($T$) with the gas equation
| $ p V = n R T $ |
the integral for the absolute temperature ($T$) is equal to the temperature in state 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Therefore,
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15760, 0)
Stirling cycle 2 to 3
Concept
In the second stage the heat supplied ($Q_H$) is added which, depending on the heat capacity at constant volume ($C_V$), increases the temperature from the temperature in state 1 ($T_1$) to the temperature in state 2 ($T_2$):
When supplying the heat supplied ($Q_H$), the temperature of the gas increases from $T_2$ to $T_3$ in an isochoric process (at constant volume). This implies that we can utilize the relationship for ($$) with the heat capacity at constant volume ($C_V$) and the variación de Temperature ($\Delta T$), expressed by the equation:
| $ dU = C_V \Delta T $ |
This results in the temperature in state 2 ($T_2$) and the temperature in state 3 ($T_3$) as follows:
| $ Q_h = C_V ( T_2 - T_1 )$ |
ID:(15761, 0)
Stirling cycle 3 to 4
Concept
In the third stage the number of moles ($n$) the gas expands making the work performed by the system ($W_{out}$) while the volume expands from the compressed volume ($V_2$) to the expanded volume ($V_1$) isothermally. to the temperature in state 2 ($T_2$):
The work is calculated using the integral of the work performed by the system ($W_{out}$) with the pressure ($p$), integrated in the volume ($V$), from the expanded volume ($V_1$) to the compressed volume ($V_2$):
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
If the pressure ($p$) is obtained using the universal gas constant ($R$), the number of moles ($n$), and the absolute temperature ($T$) with the gas equation
| $ p V = n R T $ |
the integral for the absolute temperature ($T$) is equal to the temperature in state 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Therefore,
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15762, 0)
Stirling cycle 4 to 1
Concept
In the fourth stage, the absorbed heat ($Q_C$) is reduced, which, depending on the heat capacity at constant volume ($C_V$), decreases the temperature from the temperature in state 2 ($T_2$) to the temperature in state 1 ($T_1$):
 $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
By removing the absorbed heat ($Q_C$) when the volume ($V$) equals the compressed volume ($V_2$), the absolute temperature ($T$) increases from the temperature in state 1 ($T_1$) to the temperature in state 2 ($T_2$). This implies that we can use the relationship for ($$) with the heat capacity at constant volume ($C_V$) and the variación de Temperature ($\Delta T$), which is expressed by the equation:
| $ dU = C_V \Delta T $ |
this leads us to the expression:
| $ Q_c = C_V ( T_1 - T_2 )$ |
ID:(15763, 0)
Stirling cycle performance
Concept
The efficiency ($\eta$) is defined as the ratio of the effective work ($W$) to the heat contributed to the system ($Q$):
| $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
where the effective work ($W$) is related to the work performed by the system ($W_{out}$) and the work done on the system ($W_{in}$) through:
| $ W \equiv W_{out} - W_{in} $ |
while the heat contributed to the system ($Q$) is associated with the heat supplied ($Q_H$), which is defined as:
| $ Q \equiv W_{in} + Q_h $ |
As the work performed by the system ($W_{out}$) is related to the number of moles ($n$), the temperature in state 2 ($T_2$), the expanded volume ($V_1$), the compressed volume ($V_2$), and the universal gas constant ($R$) through:
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
and the work done on the system ($W_{in}$) is associated with the temperature in state 1 ($T_1$) through:
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
and the heat supplied ($Q_H$) is linked to the heat capacity at constant volume ($C_V$) by:
| $ Q_h = C_V ( T_2 - T_1 )$ |
the efficiency ($\eta$) can be calculated, resulting in:
| $ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$ |
ID:(15764, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$
eta = ( T_2 - T_1 )/( T_1 + C_V *( T_2 - T_1 )/( n * R *log( V_2 / V_1 )))
$ \eta \equiv \displaystyle\frac{ W }{ Q } $
eta = W / Q
$ Q \equiv W_{in} + Q_h $
Q = W_in + Q_h
$ Q_c = C_V ( T_1 - T_2 )$
Q_C = C_V *( T_1 - T_2 )
$ Q_h = C_V ( T_2 - T_1 )$
Q_H = C_V *( T_2 - T_1 )
$ W \equiv W_{out} - W_{in} $
W = W_out - W_in
$ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$
W_in = n * R * T_1 * log( V_2 / V_1 )
$ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$
W_out = n * R * T_2 * log( V_2 / V_1 )
ID:(15343, 0)
Heat added to the system
Equation
The heat supplied ($Q_H$) to add depends on the heat capacity at constant volume ($C_V$) and the temperature difference from the temperature in state 1 ($T_1$) to the temperature in state 2 ($T_2$):
| $ Q_h = C_V ( T_2 - T_1 )$ |
When supplying the heat supplied ($Q_H$), the temperature of the gas increases from $T_2$ to $T_3$ in an isochoric process (at constant volume). This implies that we can utilize the relationship for ($$) with the heat capacity at constant volume ($C_V$) and the variación de Temperature ($\Delta T$), expressed by the equation:
| $ dU = C_V \Delta T $ |
This results in the temperature in state 2 ($T_2$) and the temperature in state 3 ($T_3$) as follows:
| $ Q_h = C_V ( T_2 - T_1 )$ |
ID:(15363, 0)
Isothermal expansion
Equation
The work performed by the system ($W_{out}$) is with the number of moles ($n$), the universal gas constant ($R$), the temperature in state 2 ($T_2$), the expanded volume ($V_1$) and the compressed volume ($V_2$) equal:
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
The work is calculated using the integral of the work performed by the system ($W_{out}$) with the pressure ($p$), integrated in the volume ($V$), from the expanded volume ($V_1$) to the compressed volume ($V_2$):
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
If the pressure ($p$) is obtained using the universal gas constant ($R$), the number of moles ($n$), and the absolute temperature ($T$) with the gas equation
| $ p V = n R T $ |
the integral for the absolute temperature ($T$) is equal to the temperature in state 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Therefore,
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15366, 0)
Heat removed from the system
Equation
The absorbed heat ($Q_C$) to add depends on the heat capacity at constant volume ($C_V$) and the temperature difference from the temperature in state 2 ($T_2$) to the temperature in state 1 ($T_1$):
| $ Q_c = C_V ( T_1 - T_2 )$ |
By removing the absorbed heat ($Q_C$) when the volume ($V$) equals the compressed volume ($V_2$), the absolute temperature ($T$) increases from the temperature in state 1 ($T_1$) to the temperature in state 2 ($T_2$). This implies that we can use the relationship for ($$) with the heat capacity at constant volume ($C_V$) and the variación de Temperature ($\Delta T$), which is expressed by the equation:
| $ dU = C_V \Delta T $ |
this leads us to the expression:
| $ Q_c = C_V ( T_1 - T_2 )$ |
ID:(15364, 0)
Isothermal compression
Equation
The work done on the system ($W_{in}$) is with the number of moles ($n$), the universal gas constant ($R$), the temperature in state 1 ($T_1$), the expanded volume ($V_1$) and the compressed volume ($V_2$) equal:
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
The work is calculated using the integral of the work done on the system ($W_{in}$) with the number of moles ($n$) and the pressure ($p$), integrated in the volume ($V$), from the expanded volume ($V_1$) to the compressed volume ($V_2$):
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
If the pressure ($p$) is obtained using the universal gas constant ($R$), the number of moles ($n$), and the absolute temperature ($T$) with the gas equation
| $ p V = n R T $ |
the integral for the absolute temperature ($T$) is equal to the temperature in state 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Therefore,
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15365, 0)
Effective work delivered
Equation
The effective work ($W$) comprises the work done on the system ($W_{in}$) and the work performed by the system ($W_{out}$):
| $ W \equiv W_{out} - W_{in} $ |
.
ID:(15758, 0)
Heat contributed to the system
Equation
The heat contributed to the system ($Q$) comprises the heat supplied ($Q_H$) and the work done on the system ($W_{in}$):
| $ Q \equiv W_{in} + Q_h $ |
.
ID:(15757, 0)
Performance
Equation
The efficiency ($\eta$) can be defined as the percentage that the effective work ($W$) represents in the heat contributed to the system ($Q$):
| $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
.
ID:(15756, 0)
Stirling cycle performance
Equation
The efficiency ($\eta$) of the Stirling cycle depends on the temperature in state 1 ($T_1$), the temperature in state 2 ($T_2$), the expanded volume ($V_1$), the compressed volume ($V_2$), the heat capacity at constant volume ($C_V$), the number of moles ($n$) and the universal gas constant ($R$):
| $ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$ |
The efficiency ($\eta$) is defined as the ratio of the effective work ($W$) to the heat contributed to the system ($Q$):
| $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
where the effective work ($W$) is related to the work performed by the system ($W_{out}$) and the work done on the system ($W_{in}$) through:
| $ W \equiv W_{out} - W_{in} $ |
while the heat contributed to the system ($Q$) is associated with the heat supplied ($Q_H$), which is defined as:
| $ Q \equiv W_{in} + Q_h $ |
As the work performed by the system ($W_{out}$) is related to the number of moles ($n$), the temperature in state 2 ($T_2$), the expanded volume ($V_1$), the compressed volume ($V_2$), and the universal gas constant ($R$) through:
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
and the work done on the system ($W_{in}$) is associated with the temperature in state 1 ($T_1$) through:
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
and the heat supplied ($Q_H$) is linked to the heat capacity at constant volume ($C_V$) by:
| $ Q_h = C_V ( T_2 - T_1 )$ |
the efficiency ($\eta$) can be calculated, resulting in:
| $ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$ |
.
ID:(15759, 0)