User:
The Carnot Cycle
Storyboard 
The Carnot cycle is a generic cycle in the pressure-volume space that shows how in principle a thermodynamic machine can be built that converts heat flow into mechanical work.
ID:(1488, 0)
Mechanisms
Iframe
The cycle consists of four reversible processes: two isothermal (constant temperature) and two adiabatic (no heat exchange). During the isothermal expansion, the system (typically a gas) absorbs heat from a high-temperature reservoir, expanding and doing work on the surroundings. This is followed by an adiabatic expansion where the system continues to do work but without exchanging heat, causing it to cool down. The gas then undergoes isothermal compression, releasing heat to a cooler reservoir while work is done on the gas to compress it. The cycle concludes with adiabatic compression, which further increases the temperature of the gas, returning it to its original state.
The beauty of the Carnot cycle lies in its simplicity and the insight it provides into the limits of efficiency for all heat-based engines. The efficiency of a Carnot engine depends only on the temperatures of the hot and cold reservoirs and is independent of the working substance or the details of the process itself. This efficiency is expressed as the ratio of the temperature difference between the reservoirs to the higher temperature, showing that no real engine operating between two heat reservoirs can be more efficient than a Carnot engine operating between the same reservoirs.
Mechanisms
ID:(15281, 0)
Carnot cycle: scheme of a machine
Concept
In a machine that utilizes the Carnot concept, the following processes take place:
• The reservoir with the higher temperature is created using a furnace.
• The reservoir with the lower temperature is created using a refrigeration system.
• The generated vapor from the reservoir expands into a gas, displacing the piston and raising the compensating mass. In the first isothermal stage, the first valve is open while the second valve is closed. In the second stage of the process, the first valve is closed, and the expansion continues adiabatically.
• In the third stage, the second valve is opened, and with the help of the compensating mass, the piston is returned, and the gas is expelled isothermally. In the fourth stage, the valve is closed, and the process concludes adiabatically.
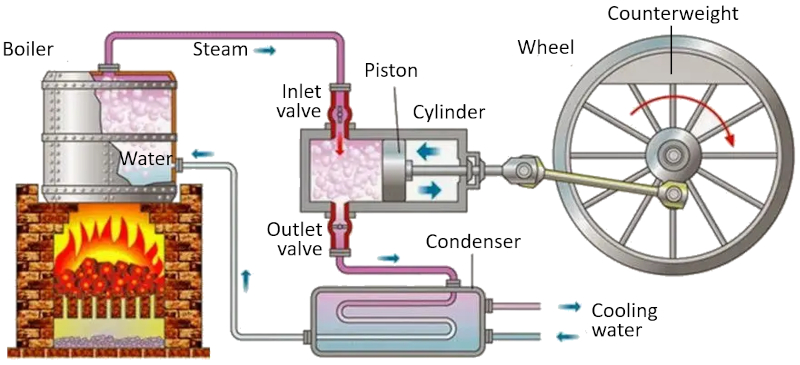
ID:(11134, 0)
Carnot cycle
Concept
Sadi Carnot introduced [1] the theoretical concept of the first machine design capable of generating mechanical work based on a heat gradient. This concept is realized through a process in the pressure-volume space where heat is added and extracted, as depicted in the image:
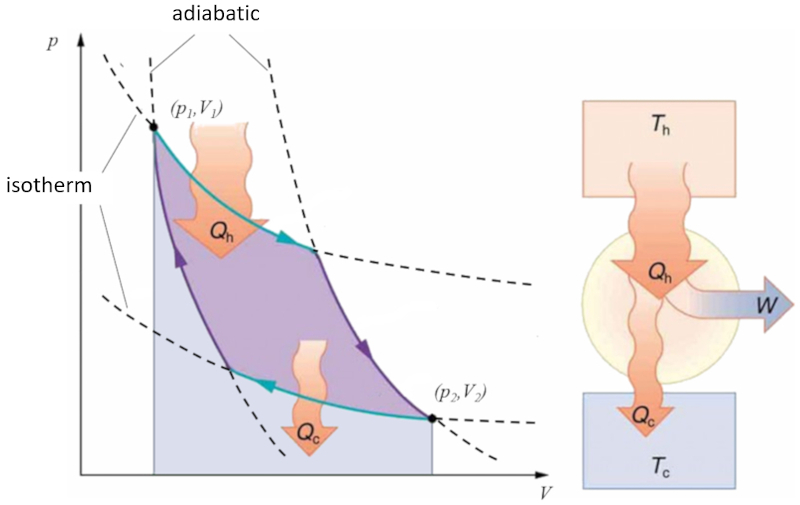
The area under curve the heat supplied ($Q_H$), spanning from 1 to 2, represents the energy input required to transition from state ($p_1, V_1$) to state ($p_2, V_2$). Conversely, the area under curve the absorbed heat ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from state ($p_2, V_2$) back to state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents the effective work ($W$) that the system can perform.
Carnot also demonstrated that, in accordance with the second law of thermodynamics, the heat supplied ($Q_H$) cannot equal zero. This implies that no machine can convert all heat into work.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflections on the Motive Power of Fire and on Machines Fitted to Develop That Power), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Application in simple pressure-volume diagram
Concept
The Carnot cycle is described simply as a cycle in which work is alternately done isothermally and adiabatically. In particular, pressure-volume and temperature-entropy diagrams are studied. In the former case, the four stages that take place can be identified as follows:
Stage 1 to 2: Isothermal expansion.
Stage 2 to 3: Adiabatic expansion.
Stage 3 to 4: Isothermal compression.
Stage 4 to 1: Adiabatic compression.
These stages are represented below:
The attached diagram illustrates the flow of energy, where the heat supplied ($Q_H$) (hot) leaves the reservoir at the high temperature ($T_H$), enters the system, performs work $W$, while the complementary absorbed heat ($Q_C$) (cold) is absorbed by the reservoir at the low temperature ($T_C$).
ID:(11132, 0)
Application in simple temperature-entropy diagram
Concept
The Carnot cycle is described simply as a cycle where work is alternately performed in an isothermal and adiabatic manner. In particular, the pressure-volume and temperature-entropy diagrams are studied. In the case of the temperature-entropy diagram, the diagram is simplified by transitioning from isothermal stages to constant entropy stages:
In the temperature-entropy diagram, the constant entropy stages are represented as follows:
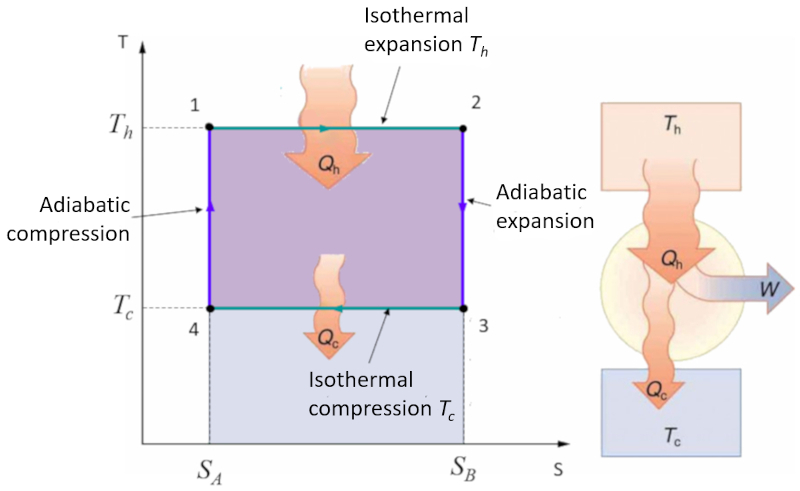
During these stages, the entropy ($S$) remains constant, implying no heat transfer, while the absolute temperature ($T$) can vary. This simplifies the cycle representation and allows for a more direct analysis of the thermodynamic properties of the system.
ID:(11133, 0)
Work done
Concept
Since the differential inexact labour ($\delta W$) is defined in terms of the pressure ($p$) and the volume Variation ($dV$) as:
| $ \delta W = p dV $ |
We can calculate the effective work ($W$) by integrating along the curves of the cycle diagram:
$W = \displaystyle\oint pdV$
Using the first law of thermodynamics with the internal energy differential ($dU$) and the differential inexact Heat ($\delta Q$):
| $ dU = \delta Q - \delta W $ |
And considering the path in the diagram of the absolute temperature ($T$) and the entropy ($S$), we obtain with the entropy variation ($dS$):
$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$
Since the integral along a closed path of an exact differential is equal to zero, we have:
| $ W = \displaystyle\oint T dS$ |
ID:(10264, 0)
Performance as a function of heat
Concept
Since the efficiency ($\eta$) with the effective work ($W$) and the heat supplied ($Q_H$) is
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
it can be replaced with the effective work ($W$) which, along with the heat supplied ($Q_H$) and the absorbed heat ($Q_C$), results in
| $ W = Q_H - Q_C $ |
yielding the following relationship:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
ID:(10262, 0)
Performance depending on temperatures
Concept
The efficiency ($\eta$) is a function of the heat supplied ($Q_H$) and the absorbed heat ($Q_C$), given by:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
We can express the heat supplied ($Q_H$) in terms of the low temperature ($T_C$), the low entropy ($S_C$), and the high entropy ($S_H$) as:
| $ Q_C = T_C ( S_H - S_C ) $ |
And using the high temperature ($T_H$) as:
| $ Q_H = T_H ( S_H - S_C ) $ |
If we substitute these expressions, we get:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
ID:(10260, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $
eta = 1 - Q_C / Q_H
$ \eta \equiv \displaystyle\frac{ W }{ Q_H } $
eta = W / Q_H
$ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $
eta =1 - T_C / T_H
$ Q_C = T_C ( S_H - S_C ) $
Q_C = T_C *( S_H - S_C )
$ Q_H = T_H ( S_H - S_C ) $
Q_H = T_H *( S_H - S_C )
$ W = Q_H - Q_C $
W = Q_H - Q_C
ID:(15340, 0)
Work generated
Equation
If, in the Carnot cycle, the heat supplied ($Q_H$) is extracted from the higher-temperature reservoir and the absorbed heat ($Q_C$) is delivered to the lower-temperature reservoir, ($$) is generated, which is equal to:
| $ W = Q_H - Q_C $ |
ID:(11135, 0)
Heat absorbed
Equation
The absorbed heat ($Q_C$) is equal to the low temperature ($T_C$) due to the difference in entropy, i.e., the high entropy ($S_H$) and the low entropy ($S_C$):
| $ Q_C = T_C ( S_H - S_C ) $ |
As the effective work ($W$) is equal to the integral along a closed path in the the absolute temperature ($T$) and the entropy ($S$) space, we have:
| $ W = \displaystyle\oint T dS$ |
Consulting the temperature-entropy graph, we can see that the absorbed heat the absorbed heat ($Q_C$) is equal to the low temperature ($T_C$) due to the difference in entropy, i.e., the high entropy ($S_H$) and the low entropy ($S_C$):
| $ Q_C = T_C ( S_H - S_C ) $ |
ID:(11138, 0)
Heat extracted
Equation
The heat supplied ($Q_H$) is equal to the high temperature ($T_H$) due to the difference in entropy, i.e., the high entropy ($S_H$) and the low entropy ($S_C$):
| $ Q_H = T_H ( S_H - S_C ) $ |
Since the effective work ($W$) is equal to the integral along a closed path in the space of the absolute temperature ($T$) and the entropy ($S$), we have:
| $ W = \displaystyle\oint T dS$ |
Consulting the temperature-entropy graph, we can see that the absorbed heat the heat supplied ($Q_H$) is equal to the high temperature ($T_H$) due to the difference in entropy, i.e., the high entropy ($S_H$) and the low entropy ($S_C$):
| $ Q_H = T_H ( S_H - S_C ) $ |
ID:(11137, 0)
Performance
Equation
The efficiency ($\eta$) can be defined as the percentage that the effective work ($W$) represents in relation to the heat supplied ($Q_H$):
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
.
ID:(11154, 0)
Performance as a function of heat
Equation
The efficiency ($\eta$) can be calculated from the heat supplied ($Q_H$) and the absorbed heat ($Q_C$) as
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Since the efficiency ($\eta$) with the effective work ($W$) and the heat supplied ($Q_H$) is
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
it can be replaced with the effective work ($W$) which, along with the heat supplied ($Q_H$) and the absorbed heat ($Q_C$), results in
| $ W = Q_H - Q_C $ |
yielding the following relationship:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
ID:(11155, 0)
Performance depending on temperatures
Equation
The efficiency ($\eta$) can be calculated based on the high temperature ($T_H$) and the low temperature ($T_C$) with:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
The efficiency ($\eta$) is a function of the heat supplied ($Q_H$) and the absorbed heat ($Q_C$), given by:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
We can express the heat supplied ($Q_H$) in terms of the low temperature ($T_C$), the low entropy ($S_C$), and the high entropy ($S_H$) as:
| $ Q_C = T_C ( S_H - S_C ) $ |
And using the high temperature ($T_H$) as:
| $ Q_H = T_H ( S_H - S_C ) $ |
If we substitute these expressions, we get:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
ID:(11136, 0)