Utilisateur:
Le cycle de Stirling
Storyboard 
Une machine thermodynamique qui n'utilise pas de combustion interne, mais qui reçoit uniquement de la chaleur provenant de l'extérieur. Ce processus génère toujours le cycle classique dans l'espace pression-volume, ce qui permet de modéliser et de calculer l'efficacité obtenue.
ID:(1485, 0)
Mécanismes
Iframe
Le cycle de Stirling comprend quatre phases principales : chauffage, expansion, refroidissement et compression, réalisées dans un environnement scellé où un gaz tel que l'hélium ou l'hydrogène sert de fluide de travail.
Durant la phase de chauffage, le gaz est chauffé à volume constant, absorbant la chaleur d'une source externe, ce qui augmente sa température et sa pression. Cette phase est suivie par l'expansion, où le gaz chauffé se dilate et effectue un travail sur un piston ou un autre mécanisme, diminuant ainsi sa température et sa pression tout en convertissant la chaleur en énergie mécanique.
Ensuite, la phase de refroidissement intervient à volume constant. Ici, le gaz perd de la chaleur, ce qui réduit sa température et sa pression, le préparant pour la phase finale. Le régénérateur joue un rôle crucial en absorbant la chaleur du gaz, ce qui conserve l'énergie et améliore l'efficacité.
Le cycle se termine par la compression du gaz refroidi, qui nécessite moins d'énergie que celle produite pendant l'expansion. Cette compression augmente la température du gaz, bien que pas autant que lors de la phase de chauffage initiale, et le cycle recommence.
Le régénérateur est vital tout au long de ce processus, stockant la chaleur de la phase de refroidissement et la restituant pendant le chauffage, réutilisant ainsi l'énergie dans le système et augmentant considérablement l'efficacité thermique du moteur. Les moteurs Stirling sont appréciés pour leur fonctionnement silencieux et la flexibilité d'utiliser n'importe quelle source de chaleur, ce qui les rend adaptables et bénéfiques pour l'environnement dans diverses applications.
Mécanismes
ID:(15284, 0)
Cycle de Carnot
Concept
Sadi Carnot a introduit [1] le concept théorique du premier projet de machine capable de générer du travail mécanique basé sur un gradient de température. Cela est réalisé grâce à un processus dans l'espace pression-volume où la chaleur est ajoutée et extraite, comme illustré dans l'image :
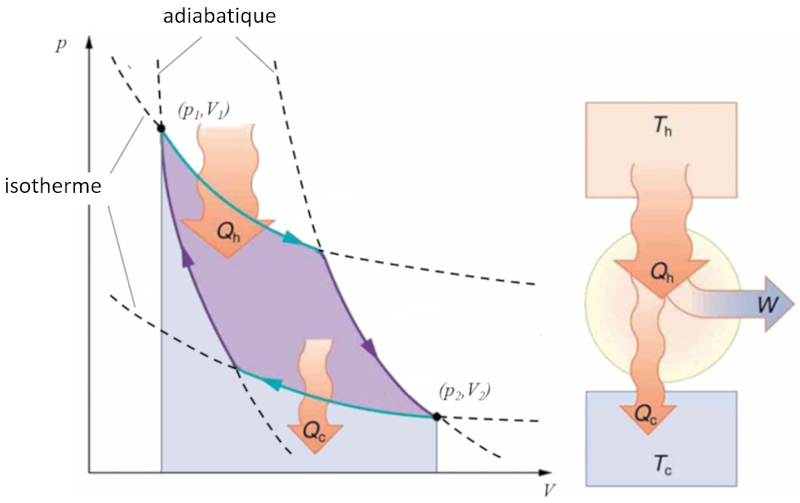
La zone sous la courbe le chaleur fournie ($Q_H$), s'étendant de 1 à 2, représente l'énergie nécessaire pour passer de l'état ($p_1, V_1$) à l'état ($p_2, V_2$). En revanche, la zone sous la courbe le chaleur absorbée ($Q_C$), allant de 2 à 1, représente l'extraction d'énergie nécessaire pour revenir de l'état ($p_2, V_2$) à l'état ($p_1, V_1$). La différence entre ces zones correspond à la région délimitée par les deux courbes et représente le travail efficace ($W$) que le système peut accomplir.
Carnot a également démontré que, conformément au deuxième principe de la thermodynamique, le chaleur fournie ($Q_H$) ne peut pas être nul. Cela implique qu'il n'existe pas de machines capables de convertir toute la chaleur en travail.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance", Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Cycle d'Stirling : diagramme pression-volume
Top
Le cycle de Stirling [1] peut être considéré comme une solution technique basée sur le cycle de Carnot, qui se compose de quatre étapes bien définies :
Phase 1 à 2 : Compression isotherme $(p_1, V_1, T_1) \rightarrow (p_2, V_2, T_1)$.
Phase 2 à 3 : Chauffage isochore $(p_2, V_2, T_1) \rightarrow (p_3, V_2, T_2)$.
Phase 3 à 4 : Expansion isotherme $(p_3, V_2, T_2) \rightarrow (p_4, V_1, T_2)$.
Phase 4 à 1 : Refroidissement isochore $(p_4, V_1, T_2) \rightarrow (p_1, V_1, T_1)$.
Il est important de noter que ce cycle n'implique pas de phase adiabatique ; il repose plutôt sur l'échange entre des processus isochores (à volume constant) et des processus isothermes (à température constante).
Ces phases peuvent être visualisées dans le diagramme suivant :
[1] "An Economical Engine for the Purpose of Pumping Water by the Expansive Force of Steam" (Un moteur économique destiné à pomper de l'eau grâce à la force expansive de la vapeur), Robert Stirling, Brevet britannique n° 4081 de 1816.
ID:(15362, 0)
Cycle Stirling 1 à 2
Concept
Dans la première étape le nombre de taupes ($n$), le gaz est comprimé avec le travail effectué sur le système ($W_{in}$) de le volume étendu ($V_1$) à Le volume compressé ($V_2$) de manière isotherme jusqu'à A température à l'état 1 ($T_1$) avec le nombre de taupes ($n$) et a pression ($p$), intégrée en le volume ($V$), de le volume étendu ($V_1$) à Le volume compressé ($V_2$) :
Si a pression ($p$) est obtenu en utilisant a constante du gaz universel ($R$), le nombre de taupes ($n$) et a température absolue ($T$) avec l'équation des gaz
l'intégrale pour a température absolue ($T$) est égale à A température à l'état 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Par conséquent,
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15760, 0)
Cycle Stirling 2 à 3
Concept
Dans la deuxième étape, le chaleur fournie ($Q_H$) est ajouté qui, en fonction de a capacité thermique à volume constant ($C_V$), augmente la température de a température à l'état 1 ($T_1$) à A température à l'état 2 ($T_2$) :
En fournissant le chaleur fournie ($Q_H$), la température du gaz augmente de $T_2$ à $T_3$ dans un processus isochore (à volume constant). Cela signifie que nous pouvons utiliser la relation pour ($$) avec a capacité thermique à volume constant ($C_V$) et ($$), exprimée par l'équation suivante :
| $ dU = C_V \Delta T $ |
Cela donne les valeurs de a température à l'état 2 ($T_2$) et a température à l'état 3 ($T_3$) comme suit :
| $ Q_h = C_V ( T_2 - T_1 )$ |
ID:(15761, 0)
Cycle Stirling 3 à 4
Concept
Dans la troisième étape le nombre de taupes ($n$), le gaz se dilate pour former le travail effectué par le système ($W_{out}$) tandis que le volume passe de le volume compressé ($V_2$) à Le volume étendu ($V_1$) de manière isotherme jusqu'à <. var>8490 :
Le travail est calculé en utilisant l'intégrale de le travail effectué par le système ($W_{out}$) avec a pression ($p$), intégrée en le volume ($V$), de le volume étendu ($V_1$) à Le volume compressé ($V_2$) :
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
Si a pression ($p$) est obtenu en utilisant a constante du gaz universel ($R$), le nombre de taupes ($n$), et a température absolue ($T$) avec l'équation des gaz
| $ p V = n R T $ |
l'intégrale pour a température absolue ($T$) est égale à A température à l'état 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Par conséquent,
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15762, 0)
Cycle Stirling 4 à 1
Concept
Dans la quatrième étape, le chaleur absorbée ($Q_C$) est réduit, ce qui, en fonction de a capacité thermique à volume constant ($C_V$), diminue la température de a température à l'état 2 ($T_2$) à A température à l'état 1 ($T_1$) :
 $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
En éliminant le chaleur absorbée ($Q_C$) lorsque le volume ($V$) est égal à volume compressé ($V_2$), a température absolue ($T$) augmente de a température à l'état 1 ($T_1$) à A température à l'état 2 ($T_2$). Cela implique que nous pouvons utiliser la relation pour ($$) avec a capacité thermique à volume constant ($C_V$) et ($$), qui est exprimée par l'équation :
| $ dU = C_V \Delta T $ |
cela nous mène à l'expression :
| $ Q_c = C_V ( T_1 - T_2 )$ |
ID:(15763, 0)
Performances du cycle de Stirling
Concept
A efficacité ($\eta$) est défini comme le rapport de le travail efficace ($W$) à Le la chaleur a contribué au système ($Q$) :
| $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
où Le travail efficace ($W$) est en relation avec le travail effectué par le système ($W_{out}$) et le travail effectué sur le système ($W_{in}$) par :
| $ W \equiv W_{out} - W_{in} $ |
tandis que le la chaleur a contribué au système ($Q$) est associé à Le chaleur fournie ($Q_H$), ce qui est défini comme :
| $ Q \equiv W_{in} + Q_h $ |
Comme le travail effectué par le système ($W_{out}$) est en relation avec le nombre de taupes ($n$), a température à l'état 2 ($T_2$), le volume étendu ($V_1$), le volume compressé ($V_2$) et a constante du gaz universel ($R$) par :
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
et le travail effectué sur le système ($W_{in}$) est associé à A température à l'état 1 ($T_1$) par :
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
et le chaleur fournie ($Q_H$) est lié à A capacité thermique à volume constant ($C_V$) par :
| $ Q_h = C_V ( T_2 - T_1 )$ |
a efficacité ($\eta$) peut être calculé, ce qui donne :
| $ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$ |
ID:(15764, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$
eta = ( T_2 - T_1 )/( T_1 + C_V *( T_2 - T_1 )/( n * R *log( V_2 / V_1 )))
$ \eta \equiv \displaystyle\frac{ W }{ Q } $
eta = W / Q
$ Q \equiv W_{in} + Q_h $
Q = W_in + Q_h
$ Q_c = C_V ( T_1 - T_2 )$
Q_C = C_V *( T_1 - T_2 )
$ Q_h = C_V ( T_2 - T_1 )$
Q_H = C_V *( T_2 - T_1 )
$ W \equiv W_{out} - W_{in} $
W = W_out - W_in
$ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$
W_in = n * R * T_1 * log( V_2 / V_1 )
$ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$
W_out = n * R * T_2 * log( V_2 / V_1 )
ID:(15343, 0)
Chaleur ajoutée au système
Équation
Le chaleur fournie ($Q_H$) à ajouter dépend de a capacité thermique à volume constant ($C_V$) et de la différence de température de a température à l'état 1 ($T_1$) à A température à l'état 2 ($T_2$) :
| $ Q_h = C_V ( T_2 - T_1 )$ |
En fournissant le chaleur fournie ($Q_H$), la température du gaz augmente de $T_2$ à $T_3$ dans un processus isochore (à volume constant). Cela signifie que nous pouvons utiliser la relation pour ($$) avec a capacité thermique à volume constant ($C_V$) et ($$), exprimée par l'équation suivante :
| $ dU = C_V \Delta T $ |
Cela donne les valeurs de a température à l'état 2 ($T_2$) et a température à l'état 3 ($T_3$) comme suit :
| $ Q_h = C_V ( T_2 - T_1 )$ |
ID:(15363, 0)
Expansion isotherme
Équation
Le travail effectué par le système ($W_{out}$) est avec le nombre de taupes ($n$), a constante du gaz universel ($R$), a température à l'état 2 ($T_2$), le volume étendu ($V_1$) et le volume compressé ($V_2$) égal :
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
Le travail est calculé en utilisant l'intégrale de le travail effectué par le système ($W_{out}$) avec a pression ($p$), intégrée en le volume ($V$), de le volume étendu ($V_1$) à Le volume compressé ($V_2$) :
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
Si a pression ($p$) est obtenu en utilisant a constante du gaz universel ($R$), le nombre de taupes ($n$), et a température absolue ($T$) avec l'équation des gaz
| $ p V = n R T $ |
l'intégrale pour a température absolue ($T$) est égale à A température à l'état 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_2}{V} dV = nRT_2\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Par conséquent,
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15366, 0)
Chaleur évacuée du système
Équation
Le chaleur absorbée ($Q_C$) à ajouter dépend de a capacité thermique à volume constant ($C_V$) et de la différence de température de a température à l'état 2 ($T_2$) à A température à l'état 1 ($T_1$) :
| $ Q_c = C_V ( T_1 - T_2 )$ |
En éliminant le chaleur absorbée ($Q_C$) lorsque le volume ($V$) est égal à volume compressé ($V_2$), a température absolue ($T$) augmente de a température à l'état 1 ($T_1$) à A température à l'état 2 ($T_2$). Cela implique que nous pouvons utiliser la relation pour ($$) avec a capacité thermique à volume constant ($C_V$) et ($$), qui est exprimée par l'équation :
| $ dU = C_V \Delta T $ |
cela nous mène à l'expression :
| $ Q_c = C_V ( T_1 - T_2 )$ |
ID:(15364, 0)
Compression isotherme
Équation
Le travail effectué sur le système ($W_{in}$) est avec le nombre de taupes ($n$), a constante du gaz universel ($R$), a température à l'état 1 ($T_1$), le volume étendu ($V_1$) et le volume compressé ($V_2$) égal :
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
Le travail est calculé à l'aide de l'intégrale de le travail effectué sur le système ($W_{in}$) avec le nombre de taupes ($n$) et a pression ($p$), intégrée en le volume ($V$), de le volume étendu ($V_1$) à Le volume compressé ($V_2$) :
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
Si a pression ($p$) est obtenu en utilisant a constante du gaz universel ($R$), le nombre de taupes ($n$) et a température absolue ($T$) avec l'équation des gaz
| $ p V = n R T $ |
l'intégrale pour a température absolue ($T$) est égale à A température à l'état 1 ($T_1$).
$W = \displaystyle\int_{V_1}^{V_2} p dV = \displaystyle\int_{V_1}^{V_2} \displaystyle\frac{nRT_1}{V} dV = nRT_1\ln\left(\displaystyle\frac{V_2}{V_1}\right)$
Par conséquent,
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
ID:(15365, 0)
Travail efficace réalisé
Équation
Le travail efficace ($W$) comprend le travail effectué sur le système ($W_{in}$) et le travail effectué par le système ($W_{out}$) :
| $ W \equiv W_{out} - W_{in} $ |
.
ID:(15758, 0)
La chaleur a contribué au système
Équation
Le la chaleur a contribué au système ($Q$) comprend le chaleur fournie ($Q_H$) et le travail effectué sur le système ($W_{in}$) :
| $ Q \equiv W_{in} + Q_h $ |
.
ID:(15757, 0)
Performance
Équation
A efficacité ($\eta$) peut être défini comme le pourcentage que le travail efficace ($W$) représente dans le la chaleur a contribué au système ($Q$) :
| $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
.
ID:(15756, 0)
Performances du cycle de Stirling
Équation
A efficacité ($\eta$) du cycle de Stirling dépend de a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), le volume étendu ($V_1$), le volume compressé ($V_2$), a capacité thermique à volume constant ($C_V$), le nombre de taupes ($n$) et a constante du gaz universel ($R$) :
| $ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$ |
A efficacité ($\eta$) est défini comme le rapport de le travail efficace ($W$) à Le la chaleur a contribué au système ($Q$) :
| $ \eta \equiv \displaystyle\frac{ W }{ Q } $ |
où Le travail efficace ($W$) est en relation avec le travail effectué par le système ($W_{out}$) et le travail effectué sur le système ($W_{in}$) par :
| $ W \equiv W_{out} - W_{in} $ |
tandis que le la chaleur a contribué au système ($Q$) est associé à Le chaleur fournie ($Q_H$), ce qui est défini comme :
| $ Q \equiv W_{in} + Q_h $ |
Comme le travail effectué par le système ($W_{out}$) est en relation avec le nombre de taupes ($n$), a température à l'état 2 ($T_2$), le volume étendu ($V_1$), le volume compressé ($V_2$) et a constante du gaz universel ($R$) par :
| $ W_{out} = n R T_2 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
et le travail effectué sur le système ($W_{in}$) est associé à A température à l'état 1 ($T_1$) par :
| $ W_{in} = n R T_1 \ln\left(\displaystyle\frac{ V_2 }{ V_1 }\right)$ |
et le chaleur fournie ($Q_H$) est lié à A capacité thermique à volume constant ($C_V$) par :
| $ Q_h = C_V ( T_2 - T_1 )$ |
a efficacité ($\eta$) peut être calculé, ce qui donne :
| $ \eta = \displaystyle\frac{ T_2 - T_1 }{ T_1 + \displaystyle\frac{ C_V ( T_2 - T_1 )}{ n R \ln( V_2 / V_1 )}}$ |
.
ID:(15759, 0)