Usuario:
El Ciclo de Otto
Storyboard 
El ciclo de Otto corresponde a un motor de combustión interna en que el calentamiento ocurre a volumen constante encendiendo la mezcla una vez se ha comprimido el gas.
ID:(1486, 0)
Mecanismos
Definición
El ciclo de Otto involucra cuatro etapas principales: admisión, compresión, expansión (o combustión) y escape. Durante la fase de admisión, el motor absorbe una mezcla de combustible y aire mientras el pistón se desplaza hacia abajo. Luego, la mezcla se comprime a medida que el pistón se mueve hacia arriba, lo que aumenta la temperatura y la presión del gas. En la cima del ciclo de compresión, la bujía enciende la mezcla comprimida, causando una combustión rápida conocida como el golpe de potencia. Esta combustión empuja el pistón hacia abajo, entregando potencia al motor.
Después del golpe de potencia, la válvula de escape se abre y el pistón se mueve hacia arriba para expulsar los gases gastados de la combustión fuera del cilindro, completando el ciclo. El motor luego repite este ciclo continuamente durante su funcionamiento.
La eficiencia de un motor que opera bajo el ciclo de Otto depende del grado de compresión y las propiedades del combustible utilizado. Relaciones de compresión más altas generalmente conducen a una mejor eficiencia pero requieren combustible de mayor octanaje para evitar la detonación del motor. El ciclo de Otto se caracteriza por ser un ciclo de alta velocidad con cada etapa claramente definida, contribuyendo significativamente a la eficiencia general y la salida de potencia de los motores que lo emplean.
ID:(15282, 0)
Ciclo de Carnot
Imagen
Sadi Carnot introduced [1] the theoretical concept of the first machine design that, based on a heat gradient, can generate mechanical work. This is achieved through a process in the pressure-volume space where heat is added and extracted, as illustrated in the image:
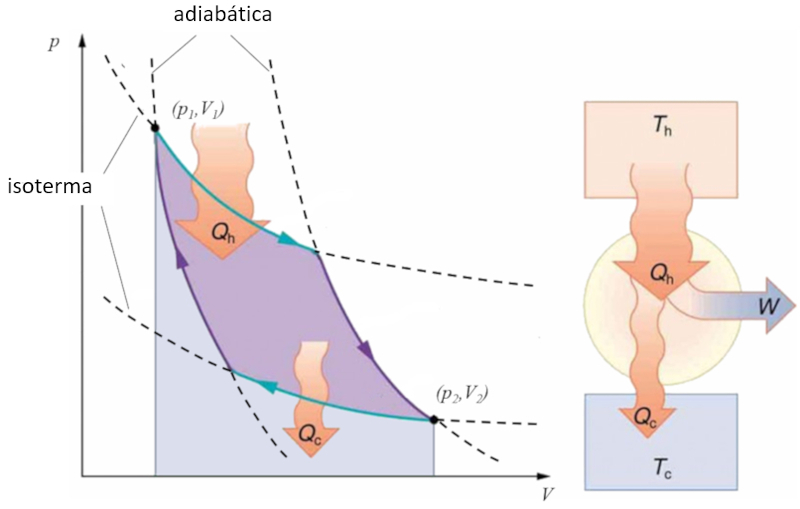
The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.
Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las máquinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Ciclo de Otto: Diagrama presión-volumen
Nota
El ciclo de Otto [1] puede considerarse como una solución técnica basada en el ciclo de Carnot. En este sentido, consta de cuatro etapas que se llevan a cabo:
• Etapa 1 a 2: Compresión adiabática $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_2)$,
• Etapa 2 a 3: Calentamiento $(p_2,V_2,T_2)\rightarrow(p_3,V_2,T_3)$,
• Etapa 3 a 4: Expansión adiabática $(p_3,V_2,T_3)\rightarrow(p_4,V_1,T_4)$,
• Etapa 4 a 1: Enfriamiento $(p_4,V_1,T_4)\rightarrow(p_1,V_1,T_1)$
Estas etapas se representan en el siguiente diagrama:
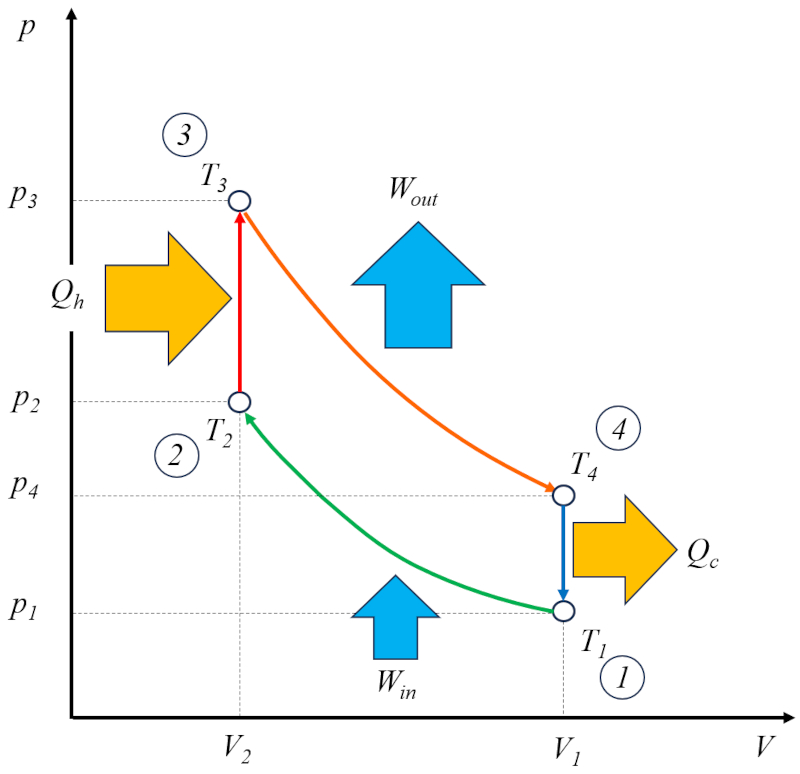
En el diagrama se muestra el flujo de energía, donde el calor suministrado ($Q_H$) añade energía, elevando la temperatura de la temperatura en estado 2 ($T_2$) a la temperatura en estado 3 ($T_3$). Ingresa al sistema y realiza un trabajo efectivo ($W$) unidades de trabajo, mientras que el complemento el calor absorbido ($Q_C$) es absorbido, disminuyendo la temperatura de la temperatura en estado 4 ($T_4$) a la temperatura en estado 1 ($T_1$).
[1] "Verbrennungsmotor" (Motor de combustión interna), N. A. Otto, Kaiserlichen Patentamts, Patente 532, 2 de enero de 1877.
Nota: En 1862, Nikolaus Otto intentó construir el motor de combustión interna patentado por Alphonse Beau de Rochas sin éxito. Más tarde lo modificó y logró construir uno funcional en 1877, fabricando 30,000 motores silenciosos y altamente confiables. Patentó su diseño en 1877; sin embargo, la patente fue revocada posteriormente debido a la existencia de la patente de Alphonse Beau de Rochas, aunque Rochas nunca logró construir su versión. Dado que Otto fue el primero en hacer funcionar el motor, su versión se recuerda hoy en día, denominando al proceso el "Ciclo de Otto".
ID:(11140, 0)
Solución técnica
Cita
El motor de Otto opera en dos ciclos: el ciclo de Otto propiamente dicho, que consta de las siguientes fases:
• Fase 1 a 2: Compresión adiabática
• Fase 2 a 3: Calentamiento
• Fase 3 a 4: Expansión adiabática
• Fase 4 a 1: Enfriamiento
Además, tiene un ciclo de vaciado de los gases quemados y llenado con una mezcla nueva.
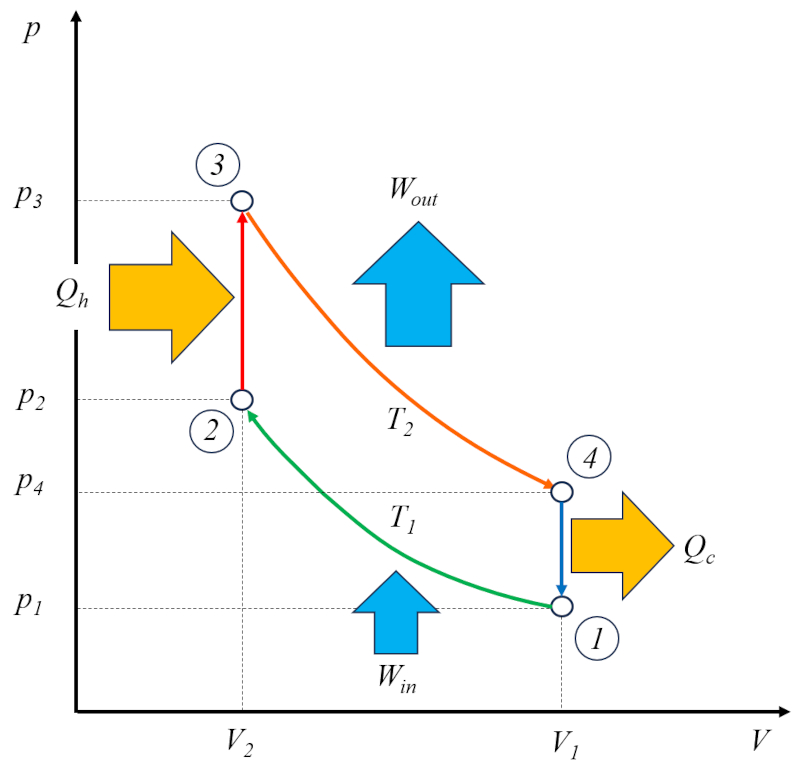
Por esta razón, se le llama un motor de dos tiempos. La fase de vaciado y llenado se puede llevar a cabo mediante una masa de compensación o a través de un segundo cilindro que opera desfasado.
La eficiencia la eficiencia ($\eta$) del motor se puede estimar utilizando el factor de compresibilidad de Otto ($r$) y el indice adiabático ($\kappa$) con la siguiente ecuación:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(11142, 0)
Eficiencia en función de las temperaturas
Ejercicio
El calor absorbido ($Q_C$) está relacionado con la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 4 ($T_4$) y la temperatura en estado 1 ($T_1$) de acuerdo con la siguiente ecuación:
| $ Q_C = C_V ( T_4 - T_1 )$ |
Mientras que el calor suministrado ($Q_H$) está relacionado con la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 2 ($T_2$) mediante la ecuación:
| $ Q_H = C_V ( T_3 - T_2 )$ |
Así, en la ecuación para la eficiencia ($\eta$) representada por:
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Tenemos la siguiente relación:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
ID:(15749, 0)
Eficiencia en función del factor de compresibilidad
Ecuación
La eficiencia ($\eta$), en función de la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$), se calcula mediante la ecuación:
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
En el caso de una expansión adiabática, se describe con el indice adiabático ($\kappa$), el volumen expandido ($V_1$) y el volumen comprimido ($V_2$) mediante la relación:
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Mientras que la compresión adiabática se representa mediante la relación:
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Si restamos la segunda ecuación de la primera, obtenemos:
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Lo cual nos lleva a la relación:
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Esto, a su vez, conduce a la definición de el factor de compresibilidad de Otto ($r$) mediante la ecuación:
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Con todos estos elementos, el rendimiento de un proceso utilizando el ciclo de Otto se puede calcular de la siguiente manera:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(15750, 0)
El Ciclo de Otto
Storyboard
El ciclo de Otto corresponde a un motor de combustión interna en que el calentamiento ocurre a volumen constante encendiendo la mezcla una vez se ha comprimido el gas.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Siguiendo una analog a al ERROR:5219,0 de l quidos y s lidos con la capacidad calórica ($C$) y la masa ($M$):
existe tambi n un calor específico de gases a volumen constante ($c_V$) para calentamiento bajo volumen constante con la capacidad calórica a volumen constante ($C_V$):
Al retirar el calor absorbido ($Q_C$), la temperatura del gas aumenta de $T_1$ a $T_4$ en un proceso isob rico (a presi n constante). Esto implica que podemos utilizar la relaci n para la variación del calor ($\Delta Q$) con la capacidad calórica a volumen constante ($C_V$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuaci n:
Esto nos lleva a los valores de la temperatura en estado 1 ($T_1$) y la temperatura en estado 4 ($T_4$) mediante la f rmula:
Al suministrar el calor suministrado ($Q_H$), la temperatura del gas aumenta de $T_2$ a $T_3$ en un proceso isoc rico (a volumen constante). Esto implica que podemos utilizar la relaci n para la variación del calor ($\Delta Q$) con la capacidad calórica a volumen constante ($C_V$) y la variación de Temperature ($\Delta T$), que se expresa mediante la ecuaci n:
Esto nos lleva a los valores de la temperatura en estado 2 ($T_2$) y la temperatura en estado 3 ($T_3$) mediante la f rmula:
En una expansi n adiab tica, el gas cumple con la relaci n que involucra el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$):
En este contexto, se pasa del punto inicial 3 al punto 4. Esto implica que durante la expansi n adiab tica, el estado del gas se modifica desde el volumen comprimido ($V_2$) y la temperatura en estado 3 ($T_3$) hasta el volumen expandido ($V_1$) y la temperatura en estado 4 ($T_4$), seg n se establece en:
Dado que en una expansi n adiab tica, el gas satisface la relaci n con el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$):
En este caso, el punto inicial 1 al punto 2. Esto significa que durante la compresi n adiab tica, el estado del gas cambia de el volumen expandido ($V_1$) y la temperatura en estado 1 ($T_1$) a el volumen comprimido ($V_2$) y la temperatura en estado 2 ($T_2$) de acuerdo con:
El calor absorbido ($Q_C$) est relacionado con la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 4 ($T_4$) y la temperatura en estado 1 ($T_1$) de acuerdo con la siguiente ecuaci n:
Mientras que el calor suministrado ($Q_H$) est relacionado con la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 2 ($T_2$) mediante la ecuaci n:
As , en la ecuaci n para la eficiencia ($\eta$) representada por:
Tenemos la siguiente relaci n:
La expansi n adiab tica se describe utilizando las variables el indice adiabático ($\kappa$), la temperatura en estado 4 ($T_4$), la temperatura en estado 3 ($T_3$), el volumen expandido ($V_1$) y el volumen comprimido ($V_2$), a trav s de la relaci n
Mientras que la compresi n adiab tica se representa con la temperatura en estado 1 ($T_1$) y la temperatura en estado 2 ($T_2$) mediante la relaci n
Al restar la segunda ecuaci n de la primera, obtenemos
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Lo que nos lleva a la relaci n
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Y esto nos permite definir el factor de compresibilidad de Otto ($r$) de la siguiente manera:
La eficiencia ($\eta$), en funci n de la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$), se calcula mediante la ecuaci n:
En el caso de una expansi n adiab tica, se describe con el indice adiabático ($\kappa$), el volumen expandido ($V_1$) y el volumen comprimido ($V_2$) mediante la relaci n:
Mientras que la compresi n adiab tica se representa mediante la relaci n:
Si restamos la segunda ecuaci n de la primera, obtenemos:
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Lo cual nos lleva a la relaci n:
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Esto, a su vez, conduce a la definici n de el factor de compresibilidad de Otto ($r$) mediante la ecuaci n:
Con todos estos elementos, el rendimiento de un proceso utilizando el ciclo de Otto se puede calcular de la siguiente manera:
Ejemplos
El ciclo de Otto involucra cuatro etapas principales: admisi n, compresi n, expansi n (o combusti n) y escape. Durante la fase de admisi n, el motor absorbe una mezcla de combustible y aire mientras el pist n se desplaza hacia abajo. Luego, la mezcla se comprime a medida que el pist n se mueve hacia arriba, lo que aumenta la temperatura y la presi n del gas. En la cima del ciclo de compresi n, la buj a enciende la mezcla comprimida, causando una combusti n r pida conocida como el golpe de potencia. Esta combusti n empuja el pist n hacia abajo, entregando potencia al motor.
Despu s del golpe de potencia, la v lvula de escape se abre y el pist n se mueve hacia arriba para expulsar los gases gastados de la combusti n fuera del cilindro, completando el ciclo. El motor luego repite este ciclo continuamente durante su funcionamiento.
La eficiencia de un motor que opera bajo el ciclo de Otto depende del grado de compresi n y las propiedades del combustible utilizado. Relaciones de compresi n m s altas generalmente conducen a una mejor eficiencia pero requieren combustible de mayor octanaje para evitar la detonaci n del motor. El ciclo de Otto se caracteriza por ser un ciclo de alta velocidad con cada etapa claramente definida, contribuyendo significativamente a la eficiencia general y la salida de potencia de los motores que lo emplean.
Sadi Carnot introduced [1] the theoretical concept of the first machine design that, based on a heat gradient, can generate mechanical work. This is achieved through a process in the pressure-volume space where heat is added and extracted, as illustrated in the image:
The area under curve el calor suministrado ($Q_H$), spanning from 1 to 2, represents the energy input required to move from the state ($p_1, V_1$) to the state ($p_2, V_2$). The area under curve el calor absorbido ($Q_C$), going from 2 to 1, represents the energy extraction needed to return from the state ($p_2, V_2$) back to the state ($p_1, V_1$). The difference between these areas corresponds to the region enclosed by both curves and represents el trabajo efectivo ($W$) that the system can perform.
Carnot also demonstrated that, due to the second law of thermodynamics, el calor suministrado ($Q_H$) cannot be zero, implying that there are no machines capable of converting all heat into work.
[1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance" (Reflexiones sobre la fuerza motriz del fuego y sobre las m quinas preparadas para desarrollar esa fuerza), Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)
El ciclo de Otto [1] puede considerarse como una soluci n t cnica basada en el ciclo de Carnot. En este sentido, consta de cuatro etapas que se llevan a cabo:
• Etapa 1 a 2: Compresi n adiab tica $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_2)$,
• Etapa 2 a 3: Calentamiento $(p_2,V_2,T_2)\rightarrow(p_3,V_2,T_3)$,
• Etapa 3 a 4: Expansi n adiab tica $(p_3,V_2,T_3)\rightarrow(p_4,V_1,T_4)$,
• Etapa 4 a 1: Enfriamiento $(p_4,V_1,T_4)\rightarrow(p_1,V_1,T_1)$
Estas etapas se representan en el siguiente diagrama:
En el diagrama se muestra el flujo de energ a, donde el calor suministrado ($Q_H$) a ade energ a, elevando la temperatura de la temperatura en estado 2 ($T_2$) a la temperatura en estado 3 ($T_3$). Ingresa al sistema y realiza un trabajo efectivo ($W$) unidades de trabajo, mientras que el complemento el calor absorbido ($Q_C$) es absorbido, disminuyendo la temperatura de la temperatura en estado 4 ($T_4$) a la temperatura en estado 1 ($T_1$).
[1] "Verbrennungsmotor" (Motor de combusti n interna), N. A. Otto, Kaiserlichen Patentamts, Patente 532, 2 de enero de 1877.
Nota: En 1862, Nikolaus Otto intent construir el motor de combusti n interna patentado por Alphonse Beau de Rochas sin xito. M s tarde lo modific y logr construir uno funcional en 1877, fabricando 30,000 motores silenciosos y altamente confiables. Patent su dise o en 1877; sin embargo, la patente fue revocada posteriormente debido a la existencia de la patente de Alphonse Beau de Rochas, aunque Rochas nunca logr construir su versi n. Dado que Otto fue el primero en hacer funcionar el motor, su versi n se recuerda hoy en d a, denominando al proceso el "Ciclo de Otto".
El motor de Otto opera en dos ciclos: el ciclo de Otto propiamente dicho, que consta de las siguientes fases:
• Fase 1 a 2: Compresi n adiab tica
• Fase 2 a 3: Calentamiento
• Fase 3 a 4: Expansi n adiab tica
• Fase 4 a 1: Enfriamiento
Adem s, tiene un ciclo de vaciado de los gases quemados y llenado con una mezcla nueva.
Por esta raz n, se le llama un motor de dos tiempos. La fase de vaciado y llenado se puede llevar a cabo mediante una masa de compensaci n o a trav s de un segundo cilindro que opera desfasado.
La eficiencia la eficiencia ($\eta$) del motor se puede estimar utilizando el factor de compresibilidad de Otto ($r$) y el indice adiabático ($\kappa$) con la siguiente ecuaci n:
El calor absorbido ($Q_C$) est relacionado con la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 4 ($T_4$) y la temperatura en estado 1 ($T_1$) de acuerdo con la siguiente ecuaci n:
Mientras que el calor suministrado ($Q_H$) est relacionado con la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 2 ($T_2$) mediante la ecuaci n:
As , en la ecuaci n para la eficiencia ($\eta$) representada por:
Tenemos la siguiente relaci n:
La eficiencia ($\eta$), en funci n de la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$), se calcula mediante la ecuaci n:
En el caso de una expansi n adiab tica, se describe con el indice adiabático ($\kappa$), el volumen expandido ($V_1$) y el volumen comprimido ($V_2$) mediante la relaci n:
Mientras que la compresi n adiab tica se representa mediante la relaci n:
Si restamos la segunda ecuaci n de la primera, obtenemos:
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Lo cual nos lleva a la relaci n:
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Esto, a su vez, conduce a la definici n de el factor de compresibilidad de Otto ($r$) mediante la ecuaci n:
Con todos estos elementos, el rendimiento de un proceso utilizando el ciclo de Otto se puede calcular de la siguiente manera:
En este caso, el punto inicial 1 al punto 2. Esto significa que durante la compresi n adiab tica, el estado del gas cambia de el volumen expandido ($V_1$) y la temperatura en estado 1 ($T_1$) a el volumen comprimido ($V_2$) y la temperatura en estado 2 ($T_2$) de acuerdo con:
El calor suministrado ($Q_H$) se puede calcular de la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 2 ($T_2$) y la temperatura en estado 3 ($T_3$) mediante la f rmula:
En este contexto, se pasa del punto inicial 3 al punto 4. Esto implica que durante la expansi n adiab tica, el estado del gas se modifica desde el volumen comprimido ($V_2$) y la temperatura en estado 3 ($T_3$) hasta el volumen expandido ($V_1$) y la temperatura en estado 4 ($T_4$), seg n se establece en:
El calor absorbido ($Q_C$) se puede calcular de la capacidad calórica a volumen constante ($C_V$), la temperatura en estado 4 ($T_4$) y la temperatura en estado 1 ($T_1$) mediante la f rmula:
La eficiencia ($\eta$) es en funci n de la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$) es igual a:
La eficiencia ($\eta$) es en ltima instancia una funci n dependiente de el volumen expandido ($V_1$) y el volumen comprimido ($V_2$), y espec ficamente, de el factor de compresibilidad de Otto ($r$):
La eficiencia ($\eta$) se puede calcular de el factor de compresibilidad de Otto ($r$) y el indice adiabático ($\kappa$) en el caso del ciclo de Otto mediante:
El calor específico de gases a volumen constante ($c_V$) es igual a la capacidad calórica a volumen constante ($C_V$) dividido por la masa ($M$):
ID:(1486, 0)