Utilisateur:
Mécanismes
Iframe 
Le cycle d'Otto comprend quatre étapes principales : l'admission, la compression, la détente (ou combustion) et l'échappement. Lors de la phase d'admission, le moteur aspire un mélange de carburant et d'air tandis que le piston descend. Ce mélange est ensuite comprimé lorsque le piston remonte, ce qui augmente la température et la pression du gaz. Au sommet du mouvement de compression, la bougie d'allumage enflamme le mélange comprimé, provoquant une combustion rapide connue sous le nom de temps moteur. Cette combustion pousse le piston vers le bas, fournissant de l'énergie au moteur.
Après le temps moteur, la soupape d'échappement s'ouvre et le piston remonte pour expulser les gaz brûlés de la combustion hors du cylindre, complétant ainsi le cycle. Le moteur répète ensuite ce cycle en continu pendant son fonctionnement.
L'efficacité d'un moteur fonctionnant selon le cycle d'Otto dépend du degré de compression et des propriétés du carburant utilisé. Des taux de compression plus élevés conduisent généralement à une meilleure efficacité, mais nécessitent un carburant à plus haut indice d'octane pour prévenir le cliquetis du moteur. Le cycle d'Otto se caractérise par sa rapidité avec chaque étape clairement définie, contribuant de manière significative à l'efficience globale et à la puissance délivrée par les moteurs qui l'utilisent.
Mécanismes
ID:(15282, 0)
Cycle de Carnot
Concept
Sadi Carnot a introduit [1] le concept théorique du premier projet de machine capable de générer du travail mécanique basé sur un gradient de température. Cela est réalisé grâce à un processus dans l'espace pression-volume où la chaleur est ajoutée et extraite, comme illustré dans l'image :
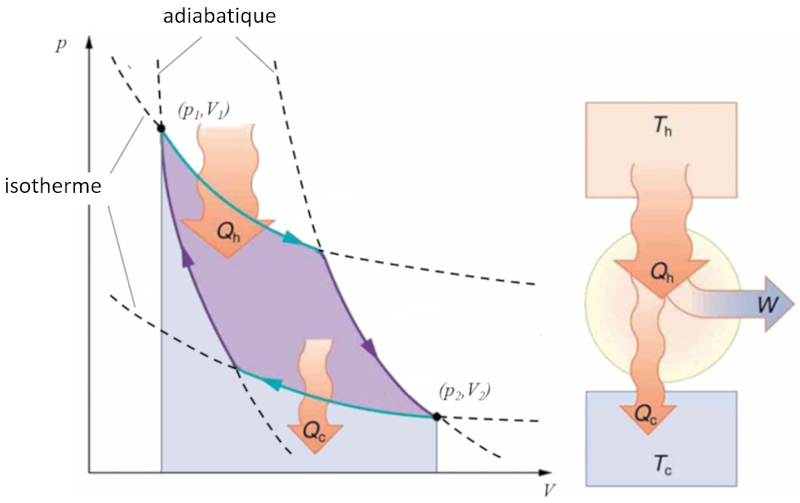
La zone sous la courbe le chaleur fournie ($Q_H$), s'étendant de 1 à 2, représente l'énergie nécessaire pour passer de l'état ($p_1, V_1$) à l'état ($p_2, V_2$). En revanche, la zone sous la courbe le chaleur absorbée ($Q_C$), allant de 2 à 1, représente l'extraction d'énergie nécessaire pour revenir de l'état ($p_2, V_2$) à l'état ($p_1, V_1$). La différence entre ces zones correspond à la région délimitée par les deux courbes et représente le travail efficace ($W$) que le système peut accomplir.
Carnot a également démontré que, conformément au deuxième principe de la thermodynamique, le chaleur fournie ($Q_H$) ne peut pas être nul. Cela implique qu'il n'existe pas de machines capables de convertir toute la chaleur en travail.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance", Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Cycle d'Otto : diagramme pression-volume
Concept
Le cycle d'Otto [1] peut être considéré comme une solution technique basée sur le cycle de Carnot. Dans ce contexte, il se compose de quatre étapes qui se déroulent comme suit :
• Étape 1 à 2 : Compression adiabatique $(p_1,V_1,T_1)\rightarrow(p_2,V_2,T_2)$,
• Étape 2 à 3 : Chauffage $(p_2,V_2,T_2)\rightarrow(p_3,V_2,T_3)$,
• Étape 3 à 4 : Expansion adiabatique $(p_3,V_2,T_3)\rightarrow(p_4,V_1,T_4)$,
• Étape 4 à 1 : Refroidissement $(p_4,V_1,T_4)\rightarrow(p_1,V_1,T_1)$
Ces étapes sont illustrées dans le diagramme suivant :
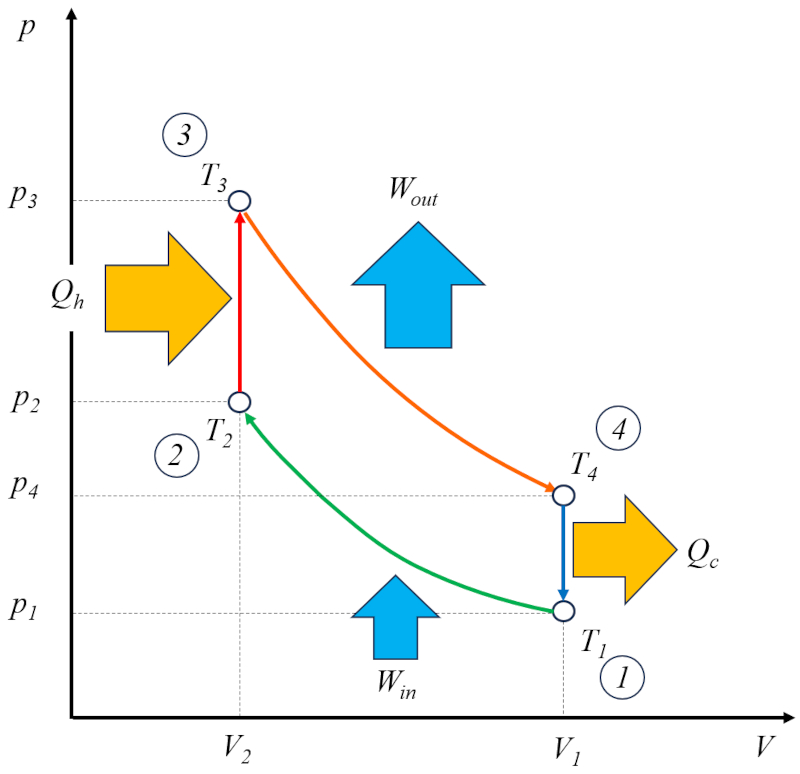
Sur le diagramme, le flux d'énergie est illustré, où Le chaleur fournie ($Q_H$) ajoute de l'énergie, faisant monter la température de a température à l'état 2 ($T_2$) à A température à l'état 3 ($T_3$). Il entre dans le système et effectue un travail efficace ($W$) unités de travail, tandis que le complément le chaleur absorbée ($Q_C$) est absorbé, abaissant la température de a température à l'état 4 ($T_4$) à A température à l'état 1 ($T_1$).
[1] "Verbrennungsmotor" (Moteur à combustion interne), N. A. Otto, Kaiserlichen Patentamts, Brevet 532, 2 janvier 1877.
Note : En 1862, Nikolaus Otto a tenté de construire le moteur à combustion interne breveté par Alphonse Beau de Rochas sans succès. Plus tard, il l'a modifié et a réussi à en construire un fonctionnel en 1877, fabriquant 30 000 moteurs silencieux et très fiables. Il a breveté son concept en 1877 ; cependant, le brevet a été révoqué ultérieurement en raison de l'existence du brevet d'Alphonse Beau de Rochas, même si Rochas n'a jamais réussi à construire sa version. Comme Otto a été le premier à faire fonctionner le moteur, sa version est aujourd'hui rappelée, désignant le processus comme le "Cycle d'Otto".
ID:(11140, 0)
Éléments d'un réfrigérateur
Concept
Le moteur Otto fonctionne selon deux cycles : le cycle Otto proprement dit, qui comprend les phases suivantes :
• Phase 1 à 2 : Compression adiabatique
• Phase 2 à 3 : Chauffage
• Phase 3 à 4 : Expansion adiabatique
• Phase 4 à 1 : Refroidissement
De plus, il possède un cycle pour vider les gaz brûlés et les remplir d'un nouveau mélange.
Pour cette raison, il est appelé un moteur deux temps. La phase de vidange et de remplissage peut être réalisée à l'aide d'une masse de compensation ou par le biais d'un second cylindre qui fonctionne en déphasage.
L'efficacité A efficacité ($\eta$) du moteur peut être estimée en utilisant le facteur de compressibilité Otto ($r$) et le indice adiabatique ($\kappa$) avec l'équation suivante :
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(11142, 0)
Efficacité en fonction des températures
Concept
Le chaleur absorbée ($Q_C$) est lié à A capacité thermique à volume constant ($C_V$), a température à l'état 4 ($T_4$) et a température à l'état 1 ($T_1$) selon l'équation suivante :
| $ Q_C = C_V ( T_4 - T_1 )$ |
Et le chaleur fournie ($Q_H$) est lié à A capacité thermique à volume constant ($C_V$), a température à l'état 3 ($T_3$) et a température à l'état 2 ($T_2$) grâce à l'équation suivante :
| $ Q_H = C_V ( T_3 - T_2 )$ |
Par conséquent, dans l'équation pour a efficacité ($\eta$) représentée par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Nous avons la relation suivante :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
ID:(15749, 0)
Efficacité en fonction du facteur de compressibilité
Concept
A efficacité ($\eta$), en fonction de a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$), est calculé à l'aide de l'équation suivante :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Dans le cas de l'expansion adiabatique, elle est décrite à l'aide de le indice adiabatique ($\kappa$), le volume étendu ($V_1$) et le volume compressé ($V_2$) avec la relation suivante :
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Et la compression adiabatique est représentée par la relation suivante :
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Si nous soustrayons la deuxième équation de la première, nous obtenons :
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Ce qui nous conduit à la relation :
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Cela nous conduit à la définition de le facteur de compressibilité Otto ($r$) avec l'équation suivante :
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Avec tous ces composants, l'efficacité d'un processus utilisant le cycle Otto peut être calculée comme suit :
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(15750, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ c_V =\displaystyle\frac{ C_V }{ M }$
c_V = C_V / M
$ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$
eta = 1 - 1/ r ^( kappa -1)
$ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$
eta =1-( T_4 - T_1 )/( T_3 - T_2 )
$ Q_C = C_V ( T_4 - T_1 )$
Q_C = C_V *( T_4 - T_1 )
$ Q_H = C_V ( T_3 - T_2 )$
Q_H = C_V *( T_3 - T_2 )
$ r =\displaystyle\frac{ V_1 }{ V_2 }$
r = V_1 / V_2
$ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$
T_1 * V_1 ^( kappa -1)= T_2 V_2 ^( kappa - 1)
$ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$
T_4 * V_1 ^( kappa -1)= T_3 V_2 ^( kappa - 1)
ID:(15341, 0)
Compression adiabatique
Équation
Dans ce cas, du point initial 1 au point 2. Cela signifie que pendant la compression adiabatique, l'état du gaz passe de le volume étendu ($V_1$) et a température à l'état 1 ($T_1$) à Le volume compressé ($V_2$) et a température à l'état 2 ($T_2$) comme suit :
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Étant donné qu'en expansion adiabatique, le gaz satisfait la relation avec le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Dans ce cas, du point initial 1 au point 2. Cela signifie que pendant la compression adiabatique, l'état du gaz passe de le volume étendu ($V_1$) et a température à l'état 1 ($T_1$) à Le volume compressé ($V_2$) et a température à l'état 2 ($T_2$) comme suit :
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
ID:(11160, 0)
Chaleur fournie
Équation
($$) peut être calculé à partir de a capacité thermique à volume constant ($C_V$), a température à l'état 2 ($T_2$) et a température à l'état 3 ($T_3$) à l'aide de la formule :
| $ Q_H = C_V ( T_3 - T_2 )$ |
En fournissant le chaleur fournie ($Q_H$), la température du gaz augmente de $T_2$ à $T_3$ dans un processus isochore (à volume constant). Cela signifie que nous pouvons utiliser la relation pour ($$) avec a capacité thermique à volume constant ($C_V$) et ($$), exprimée par l'équation suivante :
| $ dU = C_V \Delta T $ |
Cela donne les valeurs de a température à l'état 2 ($T_2$) et a température à l'état 3 ($T_3$) comme suit :
| $ Q_H = C_V ( T_3 - T_2 )$ |
ID:(11157, 0)
Expansion adiabatique
Équation
Dans ce cas, du point initial 3 au point 4. Cela signifie que pendant l'expansion adiabatique, l'état du gaz change de le volume compressé ($V_2$) et a température à l'état 3 ($T_3$) à Le volume étendu ($V_1$) et a température à l'état 4 ($T_4$) selon :
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Lors d'une expansion adiabatique, le gaz respecte la relation impliquant le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Dans ce cas, du point initial 3 au point 4. Cela signifie que pendant l'expansion adiabatique, l'état du gaz change de le volume compressé ($V_2$) et a température à l'état 3 ($T_3$) à Le volume étendu ($V_1$) et a température à l'état 4 ($T_4$) selon :
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
.
ID:(11159, 0)
Chaleur retirée
Équation
Le chaleur absorbée ($Q_C$) peut être calculé à partir de a capacité thermique à volume constant ($C_V$), a température à l'état 4 ($T_4$) et a température à l'état 1 ($T_1$) à l'aide de la formule :
| $ Q_C = C_V ( T_4 - T_1 )$ |
Lors du retrait de le chaleur absorbée ($Q_C$), la température du gaz augmente de $T_1$ à $T_4$ dans un processus isobare (à pression constante). Cela implique que nous pouvons utiliser la relation pour ($$) avec a capacité thermique à volume constant ($C_V$) et ($$), qui est exprimée par l'équation :
| $ dU = C_V \Delta T $ |
Cela nous amène aux valeurs de a température à l'état 1 ($T_1$) et a température à l'état 4 ($T_4$) en utilisant la formule :
| $ Q_C = C_V ( T_4 - T_1 )$ |
ID:(11145, 0)
Efficacité en fonction des températures
Équation
A efficacité ($\eta$) est une fonction de a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$) est égal à :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Le chaleur absorbée ($Q_C$) est lié à A capacité thermique à volume constant ($C_V$), a température à l'état 4 ($T_4$) et a température à l'état 1 ($T_1$) selon l'équation suivante :
| $ Q_C = C_V ( T_4 - T_1 )$ |
Et le chaleur fournie ($Q_H$) est lié à A capacité thermique à volume constant ($C_V$), a température à l'état 3 ($T_3$) et a température à l'état 2 ($T_2$) grâce à l'équation suivante :
| $ Q_H = C_V ( T_3 - T_2 )$ |
Par conséquent, dans l'équation pour a efficacité ($\eta$) représentée par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Nous avons la relation suivante :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
ID:(11161, 0)
Facteur de compression $r$
Équation
A efficacité ($\eta$) est finalement une fonction de le volume étendu ($V_1$) et le volume compressé ($V_2$), et en particulier, de le facteur de compressibilité Otto ($r$) :
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
L'expansion adiabatique est décrite à l'aide des variables le indice adiabatique ($\kappa$), a température à l'état 4 ($T_4$), a température à l'état 3 ($T_3$), le volume étendu ($V_1$) et le volume compressé ($V_2$) à travers la relation
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Tandis que la compression adiabatique est représentée par a température à l'état 1 ($T_1$) et a température à l'état 2 ($T_2$) à travers la relation
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
En soustrayant la deuxième équation de la première, nous obtenons
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Ce qui nous conduit à la relation
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Et cela nous permet de définir le facteur de compressibilité Otto ($r$) de la manière suivante :
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
ID:(11162, 0)
Efficacité en fonction du facteur de compressibilité
Équation
A efficacité ($\eta$) peut être calculé à partir de le facteur de compressibilité Otto ($r$) et le indice adiabatique ($\kappa$) dans le cas du cycle d'Otto en utilisant :
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
A efficacité ($\eta$), en fonction de a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$), est calculé à l'aide de l'équation suivante :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Dans le cas de l'expansion adiabatique, elle est décrite à l'aide de le indice adiabatique ($\kappa$), le volume étendu ($V_1$) et le volume compressé ($V_2$) avec la relation suivante :
| $ T_4 V_1 ^{ \kappa - 1} = T_3 V_2 ^{ \kappa - 1}$ |
Et la compression adiabatique est représentée par la relation suivante :
| $ T_1 V_1 ^{ \kappa - 1} = T_2 V_2 ^{ \kappa - 1}$ |
Si nous soustrayons la deuxième équation de la première, nous obtenons :
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Ce qui nous conduit à la relation :
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Cela nous conduit à la définition de le facteur de compressibilité Otto ($r$) avec l'équation suivante :
| $ r =\displaystyle\frac{ V_1 }{ V_2 }$ |
Avec tous ces composants, l'efficacité d'un processus utilisant le cycle Otto peut être calculée comme suit :
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
.
ID:(11163, 0)
Chaleur spécifique des gaz à volume constant
Équation
Le chaleur spécifique des gaz à volume constant ($c_V$) est égal à A capacité thermique à volume constant ($C_V$) divisé par a masse ($M$) :
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
En suivant une analogie avec le chaleur spécifique ($c$) pour les liquides et les solides avec a capacité calorique ($C$) et a masse ($M$) :
| $ c =\displaystyle\frac{ C }{ M }$ |
il existe également un chaleur spécifique des gaz à volume constant ($c_V$) pour le chauffage à volume constant avec a capacité thermique à volume constant ($C_V$) :
| $ c_V =\displaystyle\frac{ C_V }{ M }$ |
ID:(11113, 0)