Mécanismes
Définition 
Le cycle consiste en quatre processus réversibles : deux isothermes (à température constante) et deux adiabatiques (sans échange de chaleur). Lors de l'expansion isotherme, le système (généralement un gaz) absorbe de la chaleur d'un réservoir à haute température, se dilate et effectue du travail sur son environnement. Ceci est suivi d'une expansion adiabatique où le système continue de travailler mais sans échanger de chaleur, ce qui entraîne son refroidissement. Le gaz subit ensuite une compression isotherme, libérant de la chaleur vers un réservoir plus froid tout en subissant un travail de compression. Le cycle se termine par une compression adiabatique, qui augmente à nouveau la température du gaz, le ramenant à son état initial.
La beauté du cycle de Carnot réside dans sa simplicité et l'aperçu qu'il offre sur les limites de l'efficacité de tous les moteurs à chaleur. L'efficacité d'une machine de Carnot dépend uniquement des températures des réservoirs chaud et froid et est indépendante de la substance de travail ou des détails du processus lui-même. Cette efficacité est exprimée comme le rapport entre la différence de température entre les réservoirs et la température la plus élevée, démontrant qu'aucun moteur réel fonctionnant entre deux réservoirs de chaleur ne peut être plus efficace qu'une machine de Carnot opérant entre les mêmes réservoirs.
ID:(15281, 0)
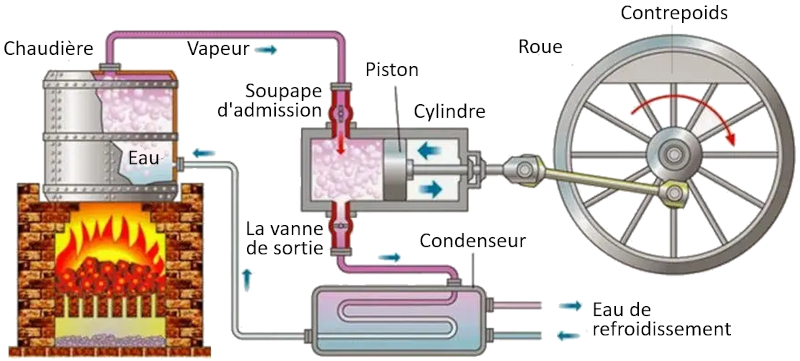
Cycle de Carnot : schéma d'une machine
Image 
Dans une machine qui utilise le concept de Carnot, les processus suivants ont lieu :
• Le réservoir à température la plus élevée est créé à l'aide d'un four.
• Le réservoir à température la plus basse est créé à l'aide d'un système de réfrigération.
• La vapeur générée à partir du réservoir se dilate en un gaz, déplaçant le piston et soulevant la masse de compensation. Dans la première étape isotherme, la première vanne est ouverte tandis que la deuxième est fermée. Dans la deuxième étape du processus, la première vanne est fermée et l'expansion se poursuit de manière adiabatique.
• Dans la troisième étape, la deuxième vanne est ouverte et, avec l'aide de la masse de compensation, le piston est ramené et le gaz est expulsé de manière isotherme. Dans la quatrième étape, la vanne est fermée et le processus se termine de manière adiabatique.
ID:(11134, 0)
Cycle de Carnot
Noter 
Sadi Carnot a introduit [1] le concept théorique du premier projet de machine capable de générer du travail mécanique basé sur un gradient de température. Cela est réalisé grâce à un processus dans l'espace pression-volume où la chaleur est ajoutée et extraite, comme illustré dans l'image :
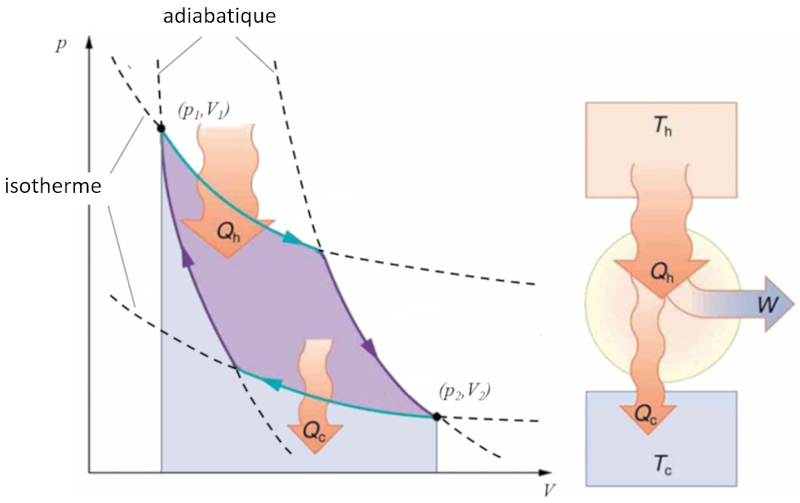
La zone sous la courbe le chaleur fournie ($Q_H$), s'étendant de 1 à 2, représente l'énergie nécessaire pour passer de l'état ($p_1, V_1$) à l'état ($p_2, V_2$). En revanche, la zone sous la courbe le chaleur absorbée ($Q_C$), allant de 2 à 1, représente l'extraction d'énergie nécessaire pour revenir de l'état ($p_2, V_2$) à l'état ($p_1, V_1$). La différence entre ces zones correspond à la région délimitée par les deux courbes et représente le travail efficace ($W$) que le système peut accomplir.
Carnot a également démontré que, conformément au deuxième principe de la thermodynamique, le chaleur fournie ($Q_H$) ne peut pas être nul. Cela implique qu'il n'existe pas de machines capables de convertir toute la chaleur en travail.
![]() [1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance", Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance", Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Application en diagramme pression-volume simple
Citation 
Le cycle de Carnot est simplement décrit comme un cycle dans lequel le travail est effectué alternativement de manière isotherme et adiabatique. En particulier, les diagrammes pression-volume et température-entropie sont étudiés. Dans le premier cas, les quatre étapes qui ont lieu peuvent être identifiées comme suit :
Étape 1 à 2 : Expansion isotherme.
Étape 2 à 3 : Expansion adiabatique.
Étape 3 à 4 : Compression isotherme.
Étape 4 à 1 : Compression adiabatique.
Ces étapes sont représentées ci-dessous :

Le diagramme ci-joint illustre le flux d'énergie, où Le chaleur fournie ($Q_H$) (chaud) quitte le réservoir à A température haute ($T_H$), entre dans le système, effectue un travail $W$, tandis que le complément ERROR:8171,0 (froid) est absorbé par le réservoir à A basse température ($T_C$).
ID:(11132, 0)
Application dans un diagramme température-entropie simple
Exercer 
Le cycle de Carnot est décrit simplement comme un cycle où le travail est effectué de manière alternée de manière isotherme et adiabatique. En particulier, on étudie les diagrammes de pression-volume et de température-entropie. Dans le cas du diagramme température-entropie, le diagramme est simplifié en passant des étapes isothermes à des étapes d'entropie constante :
Dans le diagramme température-entropie, les étapes d'entropie constante sont représentées de la manière suivante :

Pendant ces étapes, a entropie ($S$) reste constant, ce qui signifie qu'il n'y a pas de transfert de chaleur, tandis que a température absolue ($T$) peut varier. Cela simplifie la représentation du cycle et permet une analyse plus directe des propriétés thermodynamiques du système.
ID:(11133, 0)
Travail effectué
Équation 
Puisque le différentiel de travail inexact ($\delta W$) est défini en fonction de a pression ($p$) et a variation de volume ($\Delta V$) comme suit :
| $ \delta W = p dV $ |
Nous pouvons calculer le travail efficace ($W$) en intégrant le long des courbes du diagramme du cycle :
$W = \displaystyle\oint pdV$
En utilisant le premier principe de la thermodynamique avec le différentiel d'énergie interne ($dU$) et le différence de chaleur inexacte ($\delta Q$) :
| $ dU = \delta Q - \delta W $ |
Et en tenant compte du parcours dans le diagramme de a température absolue ($T$) et a entropie ($S$), nous obtenons avec a variation d'entropie ($dS$) :
$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$
Étant donné que l'intégrale le long d'un chemin fermé d'une différentielle exacte est égale à zéro, nous avons :
| $ W = \displaystyle\oint T dS$ |
ID:(10264, 0)
Performance en fonction de la chaleur
Script 
Étant donné que a efficacité ($\eta$) avec le travail efficace ($W$) et le chaleur fournie ($Q_H$) est
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
il peut être remplacé par le travail efficace ($W$) qui, avec le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donne
| $ W = Q_H - Q_C $ |
fournissant la relation suivante :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
ID:(10262, 0)
Performances en fonction des températures
Variable 
A efficacité ($\eta$) est une fonction de le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donnée par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Nous pouvons exprimer le chaleur fournie ($Q_H$) en termes de a basse température ($T_C$), a faible entropie ($S_C$), et a haute entropie ($S_H$) comme suit :
| $ Q_C = T_C ( S_H - S_C ) $ |
Et en utilisant a température haute ($T_H$) comme suit :
| $ Q_H = T_H ( S_H - S_C ) $ |
Si nous substituons ces expressions, nous obtenons :
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
ID:(10260, 0)
Le Cycle de Carnot
Description 
Variables
Calculs
Calculs
Équations
(ID 11135)
A efficacité ($\eta$) est une fonction de le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donn e par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Nous pouvons exprimer le chaleur fournie ($Q_H$) en termes de a basse température ($T_C$), a faible entropie ($S_C$), et a haute entropie ($S_H$) comme suit :
| $ Q_C = T_C ( S_H - S_C ) $ |
Et en utilisant a température haute ($T_H$) comme suit :
| $ Q_H = T_H ( S_H - S_C ) $ |
Si nous substituons ces expressions, nous obtenons :
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
(ID 11136)
tant donn que le travail efficace ($W$) est gal l'int grale le long d'un chemin ferm dans l'espace de a température absolue ($T$) et a entropie ($S$), nous avons :
| $ W = \displaystyle\oint T dS$ |
En consultant le graphique temp rature-entropie, nous pouvons voir que la chaleur absorb e le chaleur fournie ($Q_H$) est gale a température haute ($T_H$) en raison de la diff rence d'entropie, c'est- -dire a haute entropie ($S_H$) et a faible entropie ($S_C$) :
| $ Q_H = T_H ( S_H - S_C ) $ |
(ID 11137)
Comme le travail efficace ($W$) est gal l'int grale le long d'un chemin ferm dans l'espace a température absolue ($T$) et a entropie ($S$), nous avons :
| $ W = \displaystyle\oint T dS$ |
En consultant le graphique temp rature-entropie, nous pouvons voir que la chaleur absorb e le chaleur absorbée ($Q_C$) est gale a basse température ($T_C$) en raison de la diff rence d'entropie, c'est- -dire a haute entropie ($S_H$) et a faible entropie ($S_C$) :
| $ Q_C = T_C ( S_H - S_C ) $ |
(ID 11138)
tant donn que a efficacité ($\eta$) avec le travail efficace ($W$) et le chaleur fournie ($Q_H$) est
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
il peut tre remplac par le travail efficace ($W$) qui, avec le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donne
| $ W = Q_H - Q_C $ |
fournissant la relation suivante :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
(ID 11155)
Exemples
Le cycle consiste en quatre processus r versibles : deux isothermes ( temp rature constante) et deux adiabatiques (sans change de chaleur). Lors de l'expansion isotherme, le syst me (g n ralement un gaz) absorbe de la chaleur d'un r servoir haute temp rature, se dilate et effectue du travail sur son environnement. Ceci est suivi d'une expansion adiabatique o le syst me continue de travailler mais sans changer de chaleur, ce qui entra ne son refroidissement. Le gaz subit ensuite une compression isotherme, lib rant de la chaleur vers un r servoir plus froid tout en subissant un travail de compression. Le cycle se termine par une compression adiabatique, qui augmente nouveau la temp rature du gaz, le ramenant son tat initial.
La beaut du cycle de Carnot r side dans sa simplicit et l'aper u qu'il offre sur les limites de l'efficacit de tous les moteurs chaleur. L'efficacit d'une machine de Carnot d pend uniquement des temp ratures des r servoirs chaud et froid et est ind pendante de la substance de travail ou des d tails du processus lui-m me. Cette efficacit est exprim e comme le rapport entre la diff rence de temp rature entre les r servoirs et la temp rature la plus lev e, d montrant qu'aucun moteur r el fonctionnant entre deux r servoirs de chaleur ne peut tre plus efficace qu'une machine de Carnot op rant entre les m mes r servoirs.
(ID 15281)
Dans une machine qui utilise le concept de Carnot, les processus suivants ont lieu :
• Le r servoir temp rature la plus lev e est cr l'aide d'un four.
• Le r servoir temp rature la plus basse est cr l'aide d'un syst me de r frig ration.
• La vapeur g n r e partir du r servoir se dilate en un gaz, d pla ant le piston et soulevant la masse de compensation. Dans la premi re tape isotherme, la premi re vanne est ouverte tandis que la deuxi me est ferm e. Dans la deuxi me tape du processus, la premi re vanne est ferm e et l'expansion se poursuit de mani re adiabatique.
• Dans la troisi me tape, la deuxi me vanne est ouverte et, avec l'aide de la masse de compensation, le piston est ramen et le gaz est expuls de mani re isotherme. Dans la quatri me tape, la vanne est ferm e et le processus se termine de mani re adiabatique.

(ID 11134)
Sadi Carnot a introduit [1] le concept th orique du premier projet de machine capable de g n rer du travail m canique bas sur un gradient de temp rature. Cela est r alis gr ce un processus dans l'espace pression-volume o la chaleur est ajout e et extraite, comme illustr dans l'image :

La zone sous la courbe le chaleur fournie ($Q_H$), s' tendant de 1 2, repr sente l' nergie n cessaire pour passer de l' tat ($p_1, V_1$) l' tat ($p_2, V_2$). En revanche, la zone sous la courbe le chaleur absorbée ($Q_C$), allant de 2 1, repr sente l'extraction d' nergie n cessaire pour revenir de l' tat ($p_2, V_2$) l' tat ($p_1, V_1$). La diff rence entre ces zones correspond la r gion d limit e par les deux courbes et repr sente le travail efficace ($W$) que le syst me peut accomplir.
Carnot a galement d montr que, conform ment au deuxi me principe de la thermodynamique, le chaleur fournie ($Q_H$) ne peut pas tre nul. Cela implique qu'il n'existe pas de machines capables de convertir toute la chaleur en travail.
![]() [1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance", Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)
[1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance", Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)
(ID 11131)
Le cycle de Carnot est simplement d crit comme un cycle dans lequel le travail est effectu alternativement de mani re isotherme et adiabatique. En particulier, les diagrammes pression-volume et temp rature-entropie sont tudi s. Dans le premier cas, les quatre tapes qui ont lieu peuvent tre identifi es comme suit :
tape 1 2 : Expansion isotherme.
tape 2 3 : Expansion adiabatique.
tape 3 4 : Compression isotherme.
tape 4 1 : Compression adiabatique.
Ces tapes sont repr sent es ci-dessous :

Le diagramme ci-joint illustre le flux d' nergie, o le chaleur fournie ($Q_H$) (chaud) quitte le r servoir a température haute ($T_H$), entre dans le syst me, effectue un travail $W$, tandis que le compl ment ERROR:8171,0 (froid) est absorb par le r servoir a basse température ($T_C$).
(ID 11132)
Le cycle de Carnot est d crit simplement comme un cycle o le travail est effectu de mani re altern e de mani re isotherme et adiabatique. En particulier, on tudie les diagrammes de pression-volume et de temp rature-entropie. Dans le cas du diagramme temp rature-entropie, le diagramme est simplifi en passant des tapes isothermes des tapes d'entropie constante :
Dans le diagramme temp rature-entropie, les tapes d'entropie constante sont repr sent es de la mani re suivante :

Pendant ces tapes, a entropie ($S$) reste constant, ce qui signifie qu'il n'y a pas de transfert de chaleur, tandis que a température absolue ($T$) peut varier. Cela simplifie la repr sentation du cycle et permet une analyse plus directe des propri t s thermodynamiques du syst me.
(ID 11133)
Puisque le différentiel de travail inexact ($\delta W$) est d fini en fonction de a pression ($p$) et a variation de volume ($\Delta V$) comme suit :
| $ \delta W = p dV $ |
Nous pouvons calculer le travail efficace ($W$) en int grant le long des courbes du diagramme du cycle :
$W = \displaystyle\oint pdV$
En utilisant le premier principe de la thermodynamique avec le différentiel d'énergie interne ($dU$) et le différence de chaleur inexacte ($\delta Q$) :
| $ dU = \delta Q - \delta W $ |
Et en tenant compte du parcours dans le diagramme de a température absolue ($T$) et a entropie ($S$), nous obtenons avec a variation d'entropie ($dS$) :
$W = \displaystyle\oint pdV =\displaystyle\oint (\delta Q - dU) = \displaystyle\oint (TdS - dU) = \displaystyle\oint TdS - \displaystyle\oint dU$
tant donn que l'int grale le long d'un chemin ferm d'une diff rentielle exacte est gale z ro, nous avons :
| $ W = \displaystyle\oint T dS$ |
(ID 10264)
tant donn que a efficacité ($\eta$) avec le travail efficace ($W$) et le chaleur fournie ($Q_H$) est
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
il peut tre remplac par le travail efficace ($W$) qui, avec le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donne
| $ W = Q_H - Q_C $ |
fournissant la relation suivante :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
(ID 10262)
A efficacité ($\eta$) est une fonction de le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$), donn e par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
Nous pouvons exprimer le chaleur fournie ($Q_H$) en termes de a basse température ($T_C$), a faible entropie ($S_C$), et a haute entropie ($S_H$) comme suit :
| $ Q_C = T_C ( S_H - S_C ) $ |
Et en utilisant a température haute ($T_H$) comme suit :
| $ Q_H = T_H ( S_H - S_C ) $ |
Si nous substituons ces expressions, nous obtenons :
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
(ID 10260)
(ID 15340)
Si, dans le cycle de Carnot, le chaleur fournie ($Q_H$) est extrait du r servoir temp rature plus lev e et le chaleur absorbée ($Q_C$) est livr au r servoir temp rature plus basse, un travail efficace ($W$) est g n r , ce qui quivaut :
| $ W = Q_H - Q_C $ |
(ID 11135)
Le chaleur absorbée ($Q_C$) est gale a basse température ($T_C$) en raison de la diff rence d'entropie, c'est- -dire a haute entropie ($S_H$) et a faible entropie ($S_C$) :
| $ Q_C = T_C ( S_H - S_C ) $ |
(ID 11138)
Le chaleur fournie ($Q_H$) est gale a température haute ($T_H$) en raison de la diff rence d'entropie, c'est- -dire a haute entropie ($S_H$) et a faible entropie ($S_C$) :
| $ Q_H = T_H ( S_H - S_C ) $ |
(ID 11137)
A efficacité ($\eta$) peut tre d fini comme le pourcentage que repr sente le travail efficace ($W$) par rapport le chaleur fournie ($Q_H$) :
| $ \eta \equiv \displaystyle\frac{ W }{ Q_H } $ |
.
(ID 11154)
A efficacité ($\eta$) peut tre calcul partir de le chaleur fournie ($Q_H$) et le chaleur absorbée ($Q_C$) comme
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
(ID 11155)
A efficacité ($\eta$) peut tre calcul sur la base de a température haute ($T_H$) et a basse température ($T_C$) avecxa0:
| $ \eta = 1 - \displaystyle\frac{ T_C }{ T_H } $ |
(ID 11136)
ID:(1488, 0)
