Benützer:
Praktikum Absolute Temperatur
Storyboard 
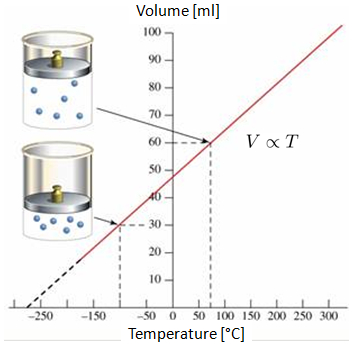
Mit Hilfe des Charles'schen Gesetzes kann die Temperatur des absoluten Nullpunkts geschätzt werden. Dazu wird bei 0 ° C ein Gasvolumen bei 100 ° C kontrahiert und nach dem Charles'schen Gesetz ist es sowohl mit Volumen als auch mit Temperaturen möglich, den absoluten Nullpunkt abzuschätzen.
ID:(1478, 0)
Experimentieren Sie, um den absoluten Nullpunkt zu schätzen
Beschreibung
Wenn das Volumen eines Gases bei 0°C und 100°C gemessen wird, zeigt sich ein lineares Verhalten im Volumen-Temperatur-Diagramm. Wenn die Gerade fortgesetzt wird, zeigt sich, dass das Volumen bei bestimmten negativen Temperaturen (in Celsius oder Fahrenheit) den Wert Null erreicht. Dieser Punkt wird als absoluter Nullpunkt bezeichnet.
Es ist wichtig zu beachten, dass in der Realität die Situation, in der das Volumen tatsächlich null wird, nicht erreicht werden kann, da alle Gase sich lange vor dem absoluten Nullpunkt kondensieren und verfestigen.
ID:(11169, 0)
Praktisch: Absolute Temperatur
Beschreibung
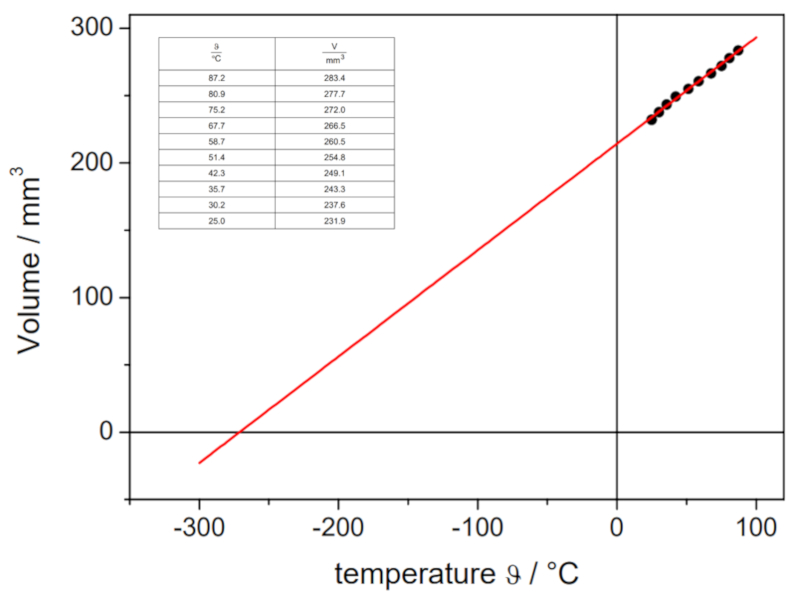
In dem folgenden Video wird gezeigt, wie im Labor die Volumina eines Gases bei unterschiedlichen Temperaturen bestimmt werden, um die Volumen-Temperatur-Kurve bei konstantem Druck zu erstellen. Durch den Schnittpunkt der Geraden mit der Temperaturachse kann die theoretische absolute Temperatur ermittelt werden, bei der das Volumen theoretisch null sein sollte:
Die erhaltenen Werte lauten:
| V [ml] | T [C] |
| 152.1 | 3.7 |
| 165.1 | 21.9 |
| 183.1 | 43.0 |
Diese werden grafisch dargestellt, einschließlich der durch Regression berechneten Geraden:
Diese Schätzung ergibt einen Wert von -148 °C, der vom tatsächlichen Wert von -273.15 °C abweicht.
ID:(11173, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$\displaystyle\frac{ V_i }{ T_i } = C_c$
V / T = C_c
$\displaystyle\frac{ V_f }{ T_f } = C_c$
V / T = C_c
$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$
V_i / T_i = V_f / T_f
ID:(15320, 0)
Charles Law (1)
Gleichung
Das Gesetz von Charles legt eine Beziehung zwischen der Volumen ($V$) und die Absolute Temperatur ($T$) fest und besagt, dass ihr Verhältnis gleich die Charles-Gesetz-Konstante ($C_c$) ist, wie folgt:
| $\displaystyle\frac{ V_i }{ T_i } = C_c$ |
| $\displaystyle\frac{ V }{ T } = C_c$ |
ID:(583, 1)
Charles Law (2)
Gleichung
Das Gesetz von Charles legt eine Beziehung zwischen der Volumen ($V$) und die Absolute Temperatur ($T$) fest und besagt, dass ihr Verhältnis gleich die Charles-Gesetz-Konstante ($C_c$) ist, wie folgt:
| $\displaystyle\frac{ V_f }{ T_f } = C_c$ |
| $\displaystyle\frac{ V }{ T } = C_c$ |
ID:(583, 2)
Zustandsänderung eines idealen Gases nach Charles Gesetz
Gleichung
Wenn ein Gas von einem Anfangszustand (i) zu einem Endzustand (f) übergeht und die Druck ($p$) konstant gehalten wird, gilt für der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$):
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Das Gesetz von Charles besagt, dass bei konstantem die Druck ($p$) das Verhältnis von der Volumen ($V$) zu die Absolute Temperatur ($T$) gleich die Charles-Gesetz-Konstante ($C_c$) ist:
| $\displaystyle\frac{ V }{ T } = C_c$ |
Dies bedeutet, dass wenn ein Gas von einem Anfangszustand (der Volumen im Zustand i ($V_i$) und die Temperatur im Ausgangszustand ($T_i$)) zu einem Endzustand (der Volumen im Zustand f ($V_f$) und die Temperatur im Endzustand ($T_f$)) übergeht und dabei die Druck ($p$) konstant gehalten wird, es immer dem Gesetz von Charles gehorchen muss:
$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$
Daher ergibt sich:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
ID:(3492, 0)