Utilisateur:
Température absolue pratique
Storyboard 
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
La loi de Charles tablit que, avec a pression ($p$) constant, le rapport de le volume ($V$) A température absolue ($T$) est gal a constante de la loi de Charles ($C_c$) :
Cela signifie que si un gaz passe d'un tat initial (le volume à l'état i ($V_i$) et a température à l'état initial ($T_i$)) un tat final (le volume à l'état f ($V_f$) et a température à l'état final ($T_f$)), en maintenant a pression ($p$) constant, il doit toujours ob ir la loi de Charles :
$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$
Ainsi, nous avons :
Exemples
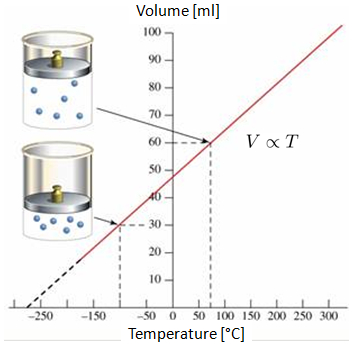
Si le volume d'un gaz est mesur 0 C et 100 C, on observe un comportement lin aire sur le graphique volume-temp rature. Si la droite est prolong e, on peut constater qu\' un certain point des temp ratures n gatives (en chelle Celsius ou Fahrenheit), le volume atteindra z ro. Ce point est appel z ro absolu.
Il est important de noter que dans la r alit , la situation o le volume atteint z ro n\'est pas atteignable, car tous les gaz se condensent et se solidifient bien avant d\'atteindre le z ro absolu.
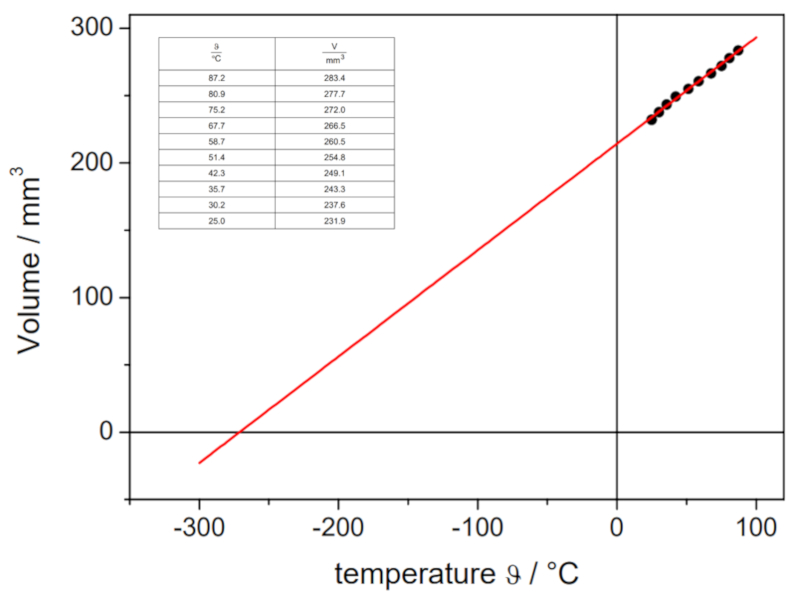
Dans la vid o suivante, on montre comment les volumes d'un gaz diff rentes temp ratures sont d termin s en laboratoire afin de tracer la courbe volume-temp rature pression constante. L'intersection de la droite avec l\'axe des temp ratures permet de d terminer la temp rature absolue th orique laquelle le volume devrait tre nul :
Les valeurs obtenues sont les suivantes :
| V [ml] | T [C] |
| 152.1 | 3.7 |
| 165.1 | 21.9 |
| 183.1 | 43.0 |
Ces valeurs sont repr sent es graphiquement, y compris la droite calcul e par r gression :
Cette estimation donne une valeur de -148 C, qui diff re de la valeur r elle de -273,15 C.
La loi de Charles tablit une relation entre le volume ($V$) et a température absolue ($T$), indiquant que leur rapport est gal a constante de la loi de Charles ($C_c$), comme suit :
La loi de Charles tablit une relation entre le volume ($V$) et a température absolue ($T$), indiquant que leur rapport est gal a constante de la loi de Charles ($C_c$), comme suit :
Si un gaz passe d'un tat initial (i) un tat final (f) avec a pression ($p$) constant, alors pour le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) :
ID:(1478, 0)
