Usuario:
Práctico Temperatura Absoluta
Storyboard 
Mediante la ley de Charles se puede estimar la temperatura del cero absoluto. Para ello se contrae un volumen de gas a 100C a 0C y con ambos volúmenes y temperaturas se puede mediante la ley de Charles estimar el cero absoluto.
ID:(1478, 0)
Experimento para estimar el cero absoluto
Descripción
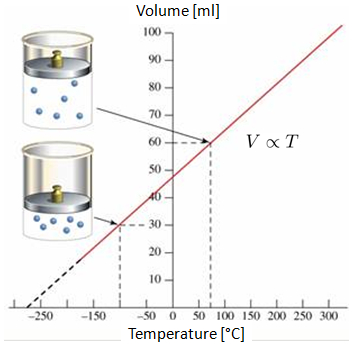
Si se mide el volumen de un gas a temperatura 0°C y a 100°C, se observa un comportamiento lineal en el gráfico volumen-temperatura. Si se proyecta la recta, se puede ver que en algún punto de las temperaturas negativas (en escala Celsius o Fahrenheit), el volumen alcanzará el volumen nulo. Este punto se denomina el cero absoluto.
Es importante destacar que en la realidad no se alcanza la situación en la que el volumen llega a cero, ya que todos los gases se condensan y se solidifican mucho antes de alcanzar el cero absoluto.
ID:(11169, 0)
Práctico: Temperatura absoluta
Descripción
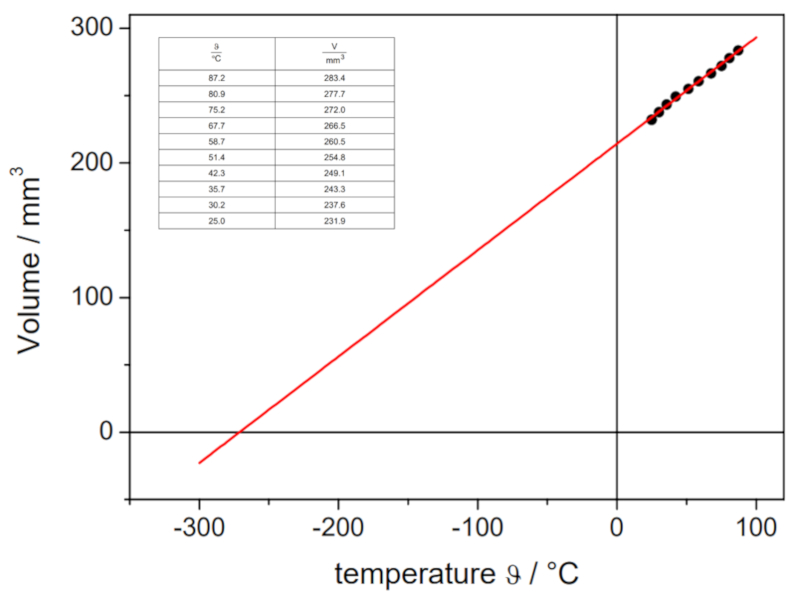
En el siguiente video se muestra cómo se determinan los volúmenes de un gas a diferentes temperaturas en el laboratorio, con el fin de trazar la curva de volumen-temperatura a presión constante. A través de la intersección de la recta con el eje de la temperatura, se puede determinar la temperatura absoluta teórica en la cual el volumen debería ser cero:
Los valores obtenidos son:
| V [ml] | T [C] |
| 152.1 | 3.7 |
| 165.1 | 21.9 |
| 183.1 | 43.0 |
Estos valores se representan gráficamente, incluyendo la recta calculada mediante regresión:
Esta estimación nos arroja un valor de -148 °C, el cual difiere del valor real de -273.15 °C.
ID:(11173, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$\displaystyle\frac{ V_i }{ T_i } = C_c$
V / T = C_c
$\displaystyle\frac{ V_f }{ T_f } = C_c$
V / T = C_c
$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$
V_i / T_i = V_f / T_f
ID:(15320, 0)
Ley de Charles (1)
Ecuación
La ley de Charles establece una relación entre el volumen ($V$) y la temperatura absoluta ($T$), indicando que su proporcion es igual a la constante de la ley de Charles ($C_c$), de la siguiente manera:
| $\displaystyle\frac{ V_i }{ T_i } = C_c$ |
| $\displaystyle\frac{ V }{ T } = C_c$ |
ID:(583, 1)
Ley de Charles (2)
Ecuación
La ley de Charles establece una relación entre el volumen ($V$) y la temperatura absoluta ($T$), indicando que su proporcion es igual a la constante de la ley de Charles ($C_c$), de la siguiente manera:
| $\displaystyle\frac{ V_f }{ T_f } = C_c$ |
| $\displaystyle\frac{ V }{ T } = C_c$ |
ID:(583, 2)
Cambio de estado de un gas ideal según la ley de Charles
Ecuación
Si un gas pasa de un estado inicial (i) a un estado final (f) con la presión ($p$) constante, se cumple que para el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$):
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
La ley de Charles establece que, con la presión ($p$) constante, se cumple que la proporción de el volumen ($V$) con la temperatura absoluta ($T$) es igual a la constante de la ley de Charles ($C_c$):
| $\displaystyle\frac{ V }{ T } = C_c$ |
Esto significa que si un gas pasa de un estado inicial (el volumen en estado i ($V_i$) y la temperatura en estado inicial ($T_i$)) a un estado final (el volumen en estado f ($V_f$) y la temperatura en estado final ($T_f$)), manteniendo la presión ($p$) constante, debe siempre cumplir la ley de Charles:
$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$
Por lo tanto, se tiene que:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
ID:(3492, 0)