Storyboard

Das Gesetz von Charles besagt, dass das Verhältnis von der Volumen ($V$) zu die Absolute Temperatur ($T$) eines Gases konstant bleibt, vorausgesetzt, dass der Druck und die Stoffmenge unverändert bleiben.

Das bedeutet, dass der Volumen ($V$) proportional zu die Absolute Temperatur ($T$) variiert.

>Modell

ID:(1473, 0)

Iframe

>Top

Das Gesetz von Charles besagt, dass das Volumen eines Gases direkt proportional zu seiner Temperatur ist, wenn der Druck konstant bleibt. Das bedeutet, dass sich das Volumen eines Gases vergrößert, wenn die Temperatur steigt, vorausgesetzt, der Druck bleibt gleich. Umgekehrt verringert sich das Volumen, wenn die Temperatur sinkt. Diese Beziehung ist grundlegend für das Verständnis des Verhaltens von Gasen und lässt sich oft beobachten, wenn ein Gas in einem flexiblen Behälter, wie einem Ballon, erwärmt oder gekühlt wird, wobei die Temperaturänderung zu einer merklichen Volumenänderung führt.

ID:(15255, 0)

Konzept

>Top

Die Erzeugung von die Druck ($p$) erfolgt, wenn Gaspartikel mit der Oberfläche des Gasbehälters kollidieren. Jede Kollision überträgt einen Impuls, der dem Zweifachen von die Partikelmasse ($m$) mal die Durchschnittsgeschwindigkeit eines Teilchens ($\bar{v}$) entspricht. Es ist auch wichtig, den Partikelstrom zur Oberfläche zu berücksichtigen, der von die Partikelkonzentration ($c_n$) abhängt, aber auch von die Durchschnittsgeschwindigkeit eines Teilchens ($\bar{v}$), mit dem sie sich bewegen. Daher gilt:

$p \propto c_n v \cdot m v = c_n m v^2$

Der Partikelstrom und die Impulsübertragung sind im folgenden Diagramm dargestellt:

Da die Partikelmasse ($m$) mal die Durchschnittsgeschwindigkeit eines Teilchens ($\bar{v}$) quadratisch proportional zur Energie ist und diese zu die Absolute Temperatur ($T$),

$mv^2 \propto E \propto T$

und da der Anzahl der Partikel ($N$) konstant ist, ist die Partikelkonzentration ($c_n$) invers proportional zu der Volumen ($V$):

$c_n \propto \displaystyle\frac{1}{V}$

Da die Druck ($p$) konstant ist, haben wir:

$p \propto \displaystyle\frac{T}{V}$

was impliziert:

$V \propto T$

ID:(15689, 0)

Beschreibung

>Top

Die Temperatur entspricht der thermischen Energie (Bewegung), die in einem Körper enthalten ist.

Da Energie immer positiv ist, können Temperaturen in Skalen wie Celsius und Fahrenheit, die negative Werte annehmen können, wenig Sinn ergeben. Die Beziehung zwischen Energie und Temperatur führt jedoch zur Schlussfolgerung, dass es eine absolute Nulltemperatur geben muss, bei der die Energie eines Systems von Teilchen gleich null ist.

Darüber hinaus beobachtete Gay-Lussac im Jahr 1802, dass es in Gasen eine proportionale Beziehung zwischen Volumen und Temperatur gibt. Diese Proportionalität impliziert, dass ein Gas ein Volumen von null bei einer Temperatur von -273,15 Grad Celsius (nach modernen Messungen) erreichen würde, was als absolute Nulltemperatur bekannt ist:

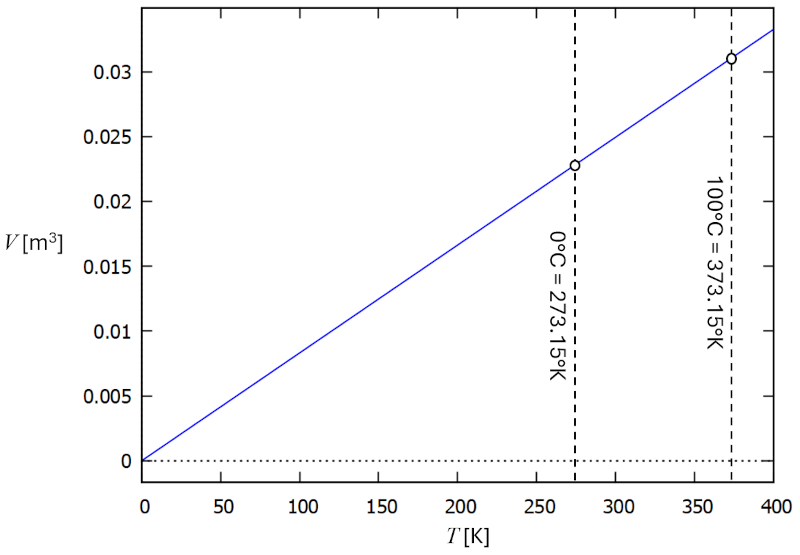
Dies impliziert die Existenz einer solchen Skala, die als absolute Temperaturskala in Kelvingraden bezeichnet wird. Andere Skalen wie Temperaturen $t$ in Celsius- oder Fahrenheitgraden können in umgerechnet werden:

Celsius:

$T = 273.15 + t$

Fahrenheit:

$T = 255.37 + \displaystyle\frac{5}{9} t$

ID:(111, 0)

Konzept

>Top

Die Temperaturdifferenz in Grad Celsius ($\Delta t$) in Kombination mit die Temperatur in Grad Celsius in Zustand 1 ($t_1$) und die Temperatur in Grad Celsius in den Zustand 2 ($t_2$) ergibt:

$\Delta t = t_2 - t_1$

Wenn wir beide Temperaturen in Kelvin ausdrücken, erhalten wir, dass die Temperatur im Zustand 1 ($T_1$) gleich ist:

$T_1 = t_1 + 273,15 , \text{K}$

und die Temperatur im Zustand 2 ($T_2$) gleich ist:

$T_2 = t_2 + 273,15 , \text{K}$

Daher wird die Differenz in Kelvin-Temperaturen, bezeichnet als die Temperaturdifferenz ($\Delta T$), wie folgt berechnet:

$\Delta T=T_2-T_1=t_2-t_1=\Delta t$

Dies impliziert:

Was bedeutet, dass der Unterschied zwischen Temperaturen in Celsius und Kelvin konstant bleibt.

ID:(15694, 0)

Beschreibung

>Top

In einem Gas, wenn die Druck ($p$) und der Anzahl der Partikel ($N$) konstant gehalten werden, beobachtet man, dass der Volumen ($V$) und die Absolute Temperatur ($T$) proportional zueinander variieren. Wenn der Volumen ($V$) abnimmt, nimmt auch die Absolute Temperatur ($T$) ab, und umgekehrt,

$V \propto T$

wie in der folgenden Grafik dargestellt:

Das Gesetz von Charles [1] besagt, dass bei konstantem die Druck ($p$) und der Anzahl der Partikel ($N$) Der Volumen ($V$) und die Absolute Temperatur ($T$) direkt proportional sind.

Dies kann mit die Charles-Gesetz-Konstante ($C_c$) wie folgt ausgedrückt werden:

[1] "Sur la dilatación de los gases y vapores" (Über die Ausdehnung von Gasen und Dämpfen), Jacques Charles, Französische Akademie der Wissenschaften (1787)

ID:(9529, 0)

Beschreibung

>Top

Jacques Charles, geboren am 12. November 1746 und gestorben am 7. April 1823, war ein französischer Physiker, Erfinder und Ballonfahrer. Er ist hauptsächlich für seine bahnbrechenden Arbeiten auf dem Gebiet der Luftfahrt und seine Entdeckungen im Zusammenhang mit dem Verhalten von Gasen bekannt. Im Jahr 1783 unternahm er gemeinsam mit dem Chemiker Nicolas-Louis Robert den ersten bemannten Flug mit einem mit Wasserstoff gefüllten Ballon. Dieser erfolgreiche Flug markierte einen wichtigen Meilenstein in der Geschichte der Luftfahrt. Charles leistete auch wichtige Beiträge zum Verständnis der Gasgesetze, einschließlich des nach ihm benannten Gesetzes von Charles, das die Beziehung zwischen Volumen und Temperatur eines Gases bei konstantem Druck beschreibt.

Hinweis: Das Gesetz von Charles wurde von Joseph Louis Gay-Lussac öffentlich gemacht, der es Jacques Charles zuschrieb und dabei auf eine unveröffentlichte Artikelquelle verwies.

ID:(1656, 0)

Konzept

>Top

Das Gesetz von Charles besagt, dass bei konstantem die Druck ($p$) das Verhältnis von der Volumen ($V$) zu die Absolute Temperatur ($T$) gleich die Charles-Gesetz-Konstante ($C_c$) ist:

Dies bedeutet, dass wenn ein Gas von einem Anfangszustand (der Volumen im Zustand i ($V_i$) und die Temperatur im Ausgangszustand ($T_i$)) zu einem Endzustand (der Volumen im Zustand f ($V_f$) und die Temperatur im Endzustand ($T_f$)) übergeht und dabei die Druck ($p$) konstant gehalten wird, es immer dem Gesetz von Charles gehorchen muss:

$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$

Daher ergibt sich:

ID:(15692, 0)

Konzept

>Top

In einem isobarischen Prozess, bei dem der Inhalt konstant bleibt, sind der Volumen im Zustand i ($V_i$), die Temperatur im Endzustand ($T_f$), die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$) durch folgende Beziehung verbunden:

Dann können wir die Dichte ($\rho$) einführen, das zusammen mit die Masse ($M$) und der Volumen ($V$) erfüllt:

Dies führt uns zu die Dichte im Zustand i ($\rho_i$) und die Dichte im Zustand f ($\rho_f$) als:

ID:(15693, 0)

Top

>Top

Parameter

$C_c$

C_c

Charles-Gesetz-Konstante

m^3/K

$M$

M

Masse

kg

Variablen

$\rho_f$

rho_f

Dichte im Zustand f

kg/m^3

$\rho_i$

rho_i

Dichte im Zustand i

kg/m^3

$T_i$

T_i

Temperatur im Ausgangszustand

K

$T_f$

T_f

Temperatur im Endzustand

K

$V_f$

V_f

Volumen im Zustand f

m^3

$V_i$

V_i

Volumen im Zustand i

m^3

Berechnungen

• Alternative Methode
• Traditionelle Methode
• Strategie
• 2D
• 3D

Gleichung

Zahl

Zuerst die Gleichung auswählen: zu , dann die Variable auswählen: zu

---

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable Gegeben Berechnen Ziel : Gleichung Zu verwenden

Gleichungen

ID:(15314, 0)

Gleichung

>Top, >Modell

Das Gesetz von Charles legt eine Beziehung zwischen der Volumen ($V$) und die Absolute Temperatur ($T$) fest und besagt, dass ihr Verhältnis gleich die Charles-Gesetz-Konstante ($C_c$) ist, wie folgt:

$\displaystyle\frac{ V_i }{ T_i } = C_c$

$\displaystyle\frac{ V }{ T } = C_c$

Bedingungen

Variablen

$T$

$T_i$

Temperatur im Ausgangszustand

$K$

5236

$C_c$

Charles-Gesetz-Konstante

$m^3/K$

9336

$V$

$V_i$

Volumen im Zustand i

$m^3$

5234

Beziehung

ID:(583, 1)

Gleichung

>Top, >Modell

Das Gesetz von Charles legt eine Beziehung zwischen der Volumen ($V$) und die Absolute Temperatur ($T$) fest und besagt, dass ihr Verhältnis gleich die Charles-Gesetz-Konstante ($C_c$) ist, wie folgt:

$\displaystyle\frac{ V_f }{ T_f } = C_c$

$\displaystyle\frac{ V }{ T } = C_c$

Bedingungen

Variablen

$T$

$T_f$

Temperatur im Endzustand

$K$

5237

$C_c$

Charles-Gesetz-Konstante

$m^3/K$

9336

$V$

$V_f$

Volumen im Zustand f

$m^3$

5235

Beziehung

ID:(583, 2)

Gleichung

>Top, >Modell

Wenn ein Gas von einem Anfangszustand (i) zu einem Endzustand (f) übergeht und die Druck ($p$) konstant gehalten wird, gilt für der Volumen im Zustand i ($V_i$), der Volumen im Zustand f ($V_f$), die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$):

$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$

Bedingungen

Variablen

$T_i$

Temperatur im Ausgangszustand

$K$

5236

$T_f$

Temperatur im Endzustand

$K$

5237

$V_f$

Volumen im Zustand f

$m^3$

5235

$V_i$

Volumen im Zustand i

$m^3$

5234

Beziehung

Entwicklung

Das Gesetz von Charles besagt, dass bei konstantem die Druck ($p$) das Verhältnis von der Volumen ($V$) zu die Absolute Temperatur ($T$) gleich die Charles-Gesetz-Konstante ($C_c$) ist:

$\displaystyle\frac{ V }{ T } = C_c$

Dies bedeutet, dass wenn ein Gas von einem Anfangszustand (der Volumen im Zustand i ($V_i$) und die Temperatur im Ausgangszustand ($T_i$)) zu einem Endzustand (der Volumen im Zustand f ($V_f$) und die Temperatur im Endzustand ($T_f$)) übergeht und dabei die Druck ($p$) konstant gehalten wird, es immer dem Gesetz von Charles gehorchen muss:

$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$

Daher ergibt sich:

$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$

ID:(3492, 0)

Gleichung

>Top, >Modell

Die Dichte ($\rho$) wird als das Verhältnis zwischen die Masse ($M$) und der Volumen ($V$) definiert, ausgedrückt als:

$ \rho_i \equiv\displaystyle\frac{ M }{ T_i }$

$ \rho \equiv\displaystyle\frac{ M }{ V }$

Bedingungen

Variablen

$\rho$

$\rho_i$

Dichte im Zustand i

$kg/m^3$

7833

$M$

Masse

$kg$

5183

$V$

$T_i$

Temperatur im Ausgangszustand

$m^3$

5236

Beziehung

Diese Eigenschaft ist spezifisch für das betreffende Material.

ID:(3704, 1)

Gleichung

>Top, >Modell

Die Dichte ($\rho$) wird als das Verhältnis zwischen die Masse ($M$) und der Volumen ($V$) definiert, ausgedrückt als:

$ \rho_f \equiv\displaystyle\frac{ M }{ T_f }$

$ \rho \equiv\displaystyle\frac{ M }{ V }$

Bedingungen

Variablen

$\rho$

$\rho_f$

Dichte im Zustand f

$kg/m^3$

7834

$M$

Masse

$kg$

5183

$V$

$T_f$

Temperatur im Endzustand

$m^3$

5237

Beziehung

Diese Eigenschaft ist spezifisch für das betreffende Material.

ID:(3704, 2)

Gleichung

>Top, >Modell

Für die Anfangszustände (die Dichte im Zustand i ($\rho_i$), der Volumen im Zustand i ($V_i$)) und Endzustände (die Dichte im Zustand f ($\rho_f$), der Volumen im Zustand f ($V_f$)) ergibt sich das Gesetz von Charles wie folgt:

$ \rho_i T_i = \rho_f T_f $

Bedingungen

Variablen

$\rho_f$

Dichte im Zustand f

$kg/m^3$

7834

$\rho_i$

Dichte im Zustand i

$kg/m^3$

7833

$T_i$

Temperatur im Ausgangszustand

$K$

5236

$T_f$

Temperatur im Endzustand

$K$

5237

Beziehung

Entwicklung

In einem isobarischen Prozess, bei dem der Inhalt konstant bleibt, sind der Volumen im Zustand i ($V_i$), die Temperatur im Endzustand ($T_f$), die Temperatur im Ausgangszustand ($T_i$) und die Temperatur im Endzustand ($T_f$) durch folgende Beziehung verbunden:

$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$

Dann können wir die Dichte ($\rho$) einführen, das zusammen mit die Masse ($M$) und der Volumen ($V$) erfüllt:

$ \rho \equiv\displaystyle\frac{ M }{ V }$

Dies führt uns zu die Dichte im Zustand i ($\rho_i$) und die Dichte im Zustand f ($\rho_f$) als:

$ \rho_i T_i = \rho_f T_f $

ID:(8835, 0)