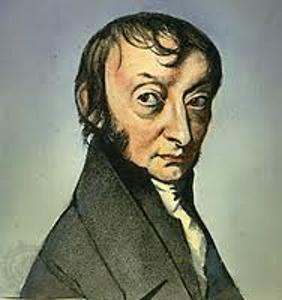Benützer:
Avogadro-Prinzip
Storyboard 
Das Avogadro-Prinzip besagt, dass die Division von der Anzahl der Mol ($n$) durch der Volumen ($V$) konstant ist, während die Druck ($p$) und die Absolute Temperatur ($T$) konstant sind.
Das bedeutet, dass der Anzahl der Mol ($n$) proportional zu der Volumen ($V$) variiert.
ID:(1475, 0)
Mechanismen
Iframe
Das Avogadro-Prinzip besagt, dass gleiche Volumina von Gasen bei gleicher Temperatur und gleichem Druck die gleiche Anzahl von Molekülen enthalten. Das bedeutet, dass das Volumen eines Gases direkt proportional zur Anzahl der vorhandenen Moleküle (oder Mol) ist, wenn Temperatur und Druck konstant gehalten werden. Dieses Prinzip ist grundlegend für das Verständnis des Verhaltens von Gasen und bildet die Grundlage des idealen Gasgesetzes. Es ermöglicht die Bestimmung der Menge an Gas in einem gegebenen Volumen und ist wesentlich für Berechnungen, die chemische Reaktionen und Gasgemische betreffen.
Mechanismen
ID:(15257, 0)
Variation von Volumen und Anzahl der Mol
Konzept
Es gibt intensive und extensive Variablen. Die ersten sind eigenständig für den Zustand des Systems und hängen nicht von seiner Größe ab. Zwei Beispiele sind die Druck ($p$) und die Absolute Temperatur ($T$). Wenn wir ein größeres System im gleichen Zustand wünschen, müssen sowohl die Druck ($p$) als auch die Absolute Temperatur ($T$) gleich bleiben.
Die Situation ist anders bei der Volumen ($V$), das eine extensive Variable ist, das bedeutet, wenn ein größeres System benötigt wird, muss sie entsprechend zunehmen. Das Gleiche gilt für der Gesamtzahl der Molen ($n$):
Zusätzlich müssen beide im gleichen Verhältnis zunehmen, also wenn die Druck ($p$) und die Absolute Temperatur ($T$) konstant sind, sind sie proportional zueinander:
$n \propto V$
ID:(15696, 0)
Mol- und Volumenverhältnis
Beschreibung
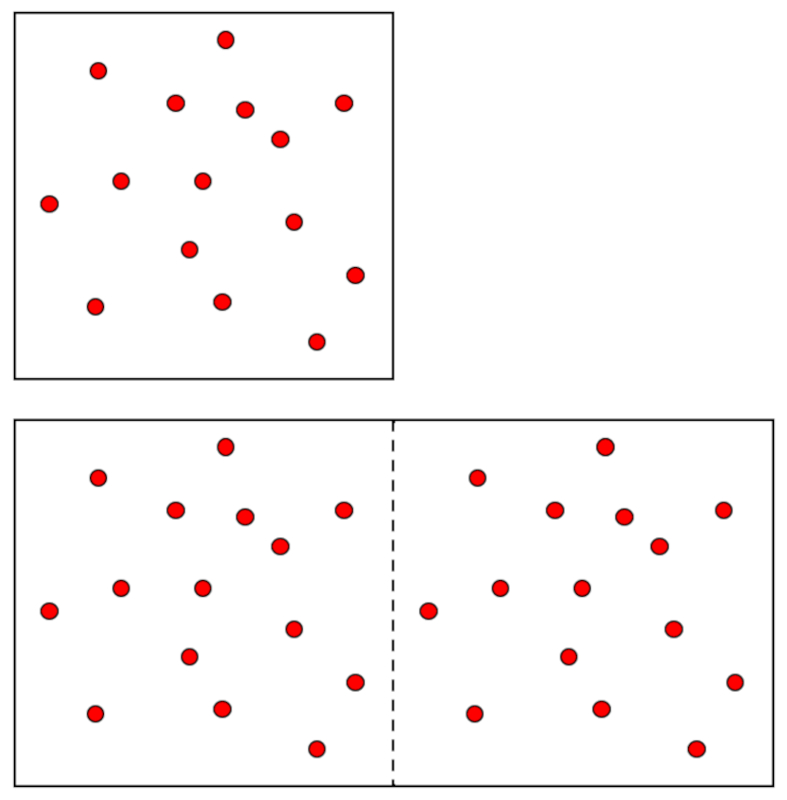
In einem Gas, wenn die Druck ($p$) und die Absolute Temperatur ($T$) konstant gehalten werden, wird eine proportionale Beziehung zwischen der Volumen ($V$) und der Anzahl der Mol ($n$) beobachtet. Jedes Mal, wenn der Volumen ($V$) zunimmt, wird festgestellt, dass auch der Anzahl der Mol ($n$) zunimmt, und umgekehrt,
$n \propto V$
wie im folgenden Diagramm dargestellt:
Das Avogadrosche Gesetz [1] besagt, dass der Volumen ($V$) und der Anzahl der Mol ($n$) direkt proportional sind, wenn die Druck ($p$) und die Absolute Temperatur ($T$) konstant gehalten werden.
Diese Beziehung kann wie folgt ausgedrückt werden, unter Verwendung von die Konstante des Avogadro-Prinzips ($C_a$):
| $\displaystyle\frac{ n }{ V } = C_a $ |
[1] "Versuch über eine Methode, die relativen Massen der Elementarmoleküle der Körper zu bestimmen und die Verhältnisse, in denen sie sich in diesen Verbindungen befinden" (Essay über eine Methode zur Bestimmung der relativen Massen der elementaren Moleküle von Körpern und der Verhältnisse, in denen sie sich in diesen Verbindungen befinden), Amedeo Avogadro, Journal de Physique, 73, 58-76 (1811).
ID:(9532, 0)
Amedeo Avogadro
Beschreibung
Amadeo Avogadro, mit vollem Namen Lorenzo Romano Amedeo Carlo Avogadro di Quaregna e di Cerreto, war ein italienischer Wissenschaftler, der am 9. August 1776 geboren wurde und am 9. Juli 1856 verstarb. Avogadro ist vor allem für seine Beiträge zur Entwicklung der Molekularteorie und zur Formulierung des Avogadro-Gesetzes bekannt. Er schlug vor, dass gleiche Volumina von Gasen bei gleicher Temperatur und Druck eine gleiche Anzahl von Teilchen enthalten, was heute als Avogadrosches Gesetz bekannt ist. Dieses Konzept war grundlegend für die Entwicklung des Stoffmengenkonzepts und legte die Grundlage für das Verständnis der Beziehungen zwischen der Menge an Stoff, dem Volumen und der Anzahl der Teilchen in Gasen. Trotz seiner bedeutenden Beiträge wurde Avogadros Arbeit zu Lebzeiten nicht weitgehend anerkannt, und seine Ideen fanden erst Jahre nach seinem Tod größere Zustimmung. Heutzutage wird Avogadro für seine grundlegenden Beiträge zur Chemie geehrt und gilt als einer der Pioniere der modernen Molekularteorie.
ID:(1659, 0)
Zustandsänderung eines idealen Gases nach dem Avogadro-Gesetz
Konzept
Das Avogadro-Prinzip besagt, dass wenn die Druck ($p$) und die Absolute Temperatur ($T$) konstant gehalten werden, das Verhältnis von Número de Moles ($n$) zu der Volumen ($V$) gleich die Konstante des Avogadro-Prinzips ($C_a$) ist:
| $\displaystyle\frac{ n }{ V } = C_a $ |
Das bedeutet, dass wenn ein Gas von einem Anfangszustand (der Anzahl der Maulwürfe im Staat i ($n_i$) und der Volumen im Zustand i ($V_i$)) zu einem Endzustand (der Anzahl der Maulwürfe im Staat f ($n_f$) und der Volumen im Zustand f ($V_f$)) übergeht, während die Druck ($p$) und die Absolute Temperatur ($T$) konstant gehalten werden, das Gay-Lussac-Gesetz immer gilt:
$\displaystyle\frac{n_i}{V_i}=C_a=\displaystyle\frac{n_f}{V_f}$
Daher haben wir:
| $\displaystyle\frac{ n_i }{ V_i }=\displaystyle\frac{ n_f }{ V_f }$ |
ID:(15695, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$\displaystyle\frac{ n_i }{ V_i } = C_a $
n / V = C_a
$\displaystyle\frac{ n_f }{ V_f } = C_a $
n / V = C_a
$\displaystyle\frac{ n_i }{ V_i }=\displaystyle\frac{ n_f }{ V_f }$
n_i / V_i = n_f / V_f
ID:(15316, 0)
Avogadro-Gesetz (1)
Gleichung
Das Avogadrosche Gesetz besagt, dass der Volumen ($V$) und der Anzahl der Mol ($n$) direkt proportional sind, wenn die Druck ($p$) und die Absolute Temperatur ($T$) konstant gehalten werden.
Diese Beziehung kann wie folgt ausgedrückt werden, unter Verwendung von die Konstante des Avogadro-Prinzips ($C_a$):
| $\displaystyle\frac{ n_i }{ V_i } = C_a $ |
| $\displaystyle\frac{ n }{ V } = C_a $ |
ID:(580, 1)
Avogadro-Gesetz (2)
Gleichung
Das Avogadrosche Gesetz besagt, dass der Volumen ($V$) und der Anzahl der Mol ($n$) direkt proportional sind, wenn die Druck ($p$) und die Absolute Temperatur ($T$) konstant gehalten werden.
Diese Beziehung kann wie folgt ausgedrückt werden, unter Verwendung von die Konstante des Avogadro-Prinzips ($C_a$):
| $\displaystyle\frac{ n_f }{ V_f } = C_a $ |
| $\displaystyle\frac{ n }{ V } = C_a $ |
ID:(580, 2)
Zustandsänderung eines idealen Gases nach dem Avogadro-Gesetz
Gleichung
Wenn ein Gas von einem Anfangszustand (i) zu einem Endzustand (f) übergeht und dabei die Druck ($p$) und die Absolute Temperatur ($T$) konstant gehalten werden, gilt für der Anzahl der Maulwürfe im Staat i ($n_i$), der Volumen im Zustand i ($V_i$), der Anzahl der Maulwürfe im Staat f ($n_f$) und der Volumen im Zustand f ($V_f$) :
| $\displaystyle\frac{ n_i }{ V_i }=\displaystyle\frac{ n_f }{ V_f }$ |
Das Avogadro-Prinzip besagt, dass wenn die Druck ($p$) und die Absolute Temperatur ($T$) konstant gehalten werden, das Verhältnis von Número de Moles ($n$) zu der Volumen ($V$) gleich die Konstante des Avogadro-Prinzips ($C_a$) ist:
| $\displaystyle\frac{ n }{ V } = C_a $ |
Das bedeutet, dass wenn ein Gas von einem Anfangszustand (der Anzahl der Maulwürfe im Staat i ($n_i$) und der Volumen im Zustand i ($V_i$)) zu einem Endzustand (der Anzahl der Maulwürfe im Staat f ($n_f$) und der Volumen im Zustand f ($V_f$)) übergeht, während die Druck ($p$) und die Absolute Temperatur ($T$) konstant gehalten werden, das Gay-Lussac-Gesetz immer gilt:
$\displaystyle\frac{n_i}{V_i}=C_a=\displaystyle\frac{n_f}{V_f}$
Daher haben wir:
| $\displaystyle\frac{ n_i }{ V_i }=\displaystyle\frac{ n_f }{ V_f }$ |
ID:(3489, 0)