Loi Charles
Storyboard 
La loi de Charles établit que le quotient entre le volume ($V$) et a température absolue ($T$) d'un gaz est constant, à condition que la pression et la quantité de moles restent inchangées.
Cela implique que le volume ($V$) varie de manière proportionnelle à A température absolue ($T$).
ID:(1473, 0)
Mécanismes
Iframe 
La loi de Charles stipule que le volume d'un gaz est directement proportionnel à sa température lorsque la pression reste constante. Cela signifie que, lorsque la température d'un gaz augmente, son volume augmente également, à condition que la pression reste la même. Inversement, si la température diminue, le volume diminue également. Cette relation est fondamentale pour comprendre le comportement des gaz et est souvent observée lorsqu'on chauffe ou refroidit un gaz dans un contenant flexible, comme un ballon, où le changement de température entraîne une variation notable du volume.
Mécanismes
ID:(15255, 0)
Variation de volume et de température
Concept 
La génération de a pression ($p$) se produit lorsque les particules de gaz entrent en collision avec la surface du récipient de gaz. Chaque collision transmet un moment égal au double de a masse molaire ($m$) fois a vitesse moyenne d'une particule ($\bar{v}$). De plus, il est important de considérer le flux de particules vers la surface, qui dépend de a concentration de particules ($c_n$) mais aussi de a vitesse moyenne d'une particule ($\bar{v}$), avec lequel elles se déplacent. Par conséquent,
$p \propto c_n v \cdot m v = c_n m v^2$
Le flux de particules et la transmission du moment sont représentés dans le graphique suivant :

Étant donné que a masse molaire ($m$) fois a vitesse moyenne d'une particule ($\bar{v}$) au carré est proportionnel à l'énergie, et cette dernière à A température absolue ($T$),
$mv^2 \propto E \propto T$
et, étant donné que le nombre de particules ($N$) est constant, a concentration de particules ($c_n$) est inversement proportionnel à Le volume ($V$) :
$c_n \propto \displaystyle\frac{1}{V}$
Comme a pression ($p$) est constante, nous avons :
$p \propto \displaystyle\frac{T}{V}$
ce qui implique :
$V \propto T$
ID:(15689, 0)
Signification de la température absolue
Description 
La température correspond à l'énergie thermique (mouvement) contenue dans un objet.
Puisque l'énergie est toujours positive, les échelles de température telles que Celsius et Fahrenheit, qui peuvent prendre des valeurs négatives, peuvent sembler contre-intuitives. Cependant, la relation entre l'énergie et la température conduit à la conclusion qu'il doit exister une température minimale, connue sous le nom de zéro absolu, où l'énergie d'un système de particules est nulle.
De plus, en 1802, Gay-Lussac a observé que dans les gaz, il existe une relation proportionnelle entre le volume et la température. Cette proportionnalité implique qu'un gaz atteindrait un volume nul à une température de -273,15 degrés Celsius (selon les mesures modernes), ce qui est connu sous le nom de zéro absolu de température:
Cela implique l'existence d'une telle échelle, qui a été appelée l'échelle de température absolue mesurée en degrés Kelvin. D'autres échelles, telles que les températures $t$ en degrés Celsius ou Fahrenheit, peuvent être converties en
Celsius:
$T = 273.15 + t$
Fahrenheit:
$T = 255.37 + \displaystyle\frac{5}{9} t$
ID:(111, 0)
Égalité des différences de température Celsius et Kelvin
Concept 
A différence de température en degrés Celsius ($\Delta t$) combiné à A température en degrés Celsius à l'état 1 ($t_1$) et a température en degrés Celsius à l'état 2 ($t_2$) donne comme résultat :
$\Delta t = t_2 - t_1$
Si nous exprimons les deux températures en degrés Kelvin, nous avons que a température à l'état 1 ($T_1$) est égal à :
$T_1 = t_1 + 273.15 , \text{K}$
et a température à l'état 2 ($T_2$) est égal à :
$T_2 = t_2 + 273.15 , \text{K}$
Par conséquent, la différence de températures en Kelvin, désignée par a différence de température ($\Delta T$), se calcule comme suit :
$\Delta T=T_2-T_1=t_2-t_1=\Delta t$
Cela implique :
| $ \Delta T = \Delta t $ |
Ce qui signifie que la différence entre les températures en degrés Celsius et Kelvin reste la même.
ID:(15694, 0)
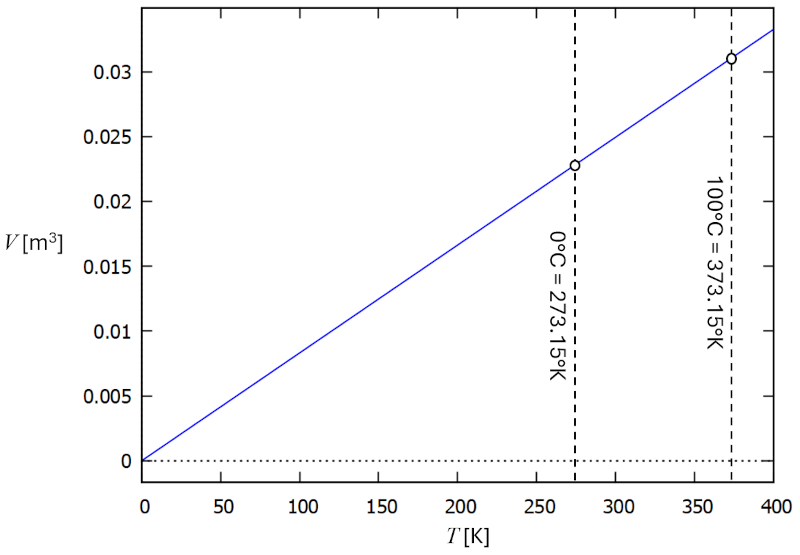
Relation température vs volume
Description 
Dans un gaz, si a pression ($p$) et le nombre de particules ($N$) sont maintenus constants, on observe que le volume ($V$) et a température absolue ($T$) varient de manière proportionnelle. Lorsque le volume ($V$) diminue, a température absolue ($T$) diminue également, et vice versa,
$V \propto T$
comme illustré dans le graphique suivant :

La loi de Charles [1] stipule qu'avec a pression ($p$) et le nombre de particules ($N$) constants, le volume ($V$) et a température absolue ($T$) sont directement proportionnels.
Cela peut être exprimé avec a constante de la loi de Charles ($C_c$) comme suit :
| $\displaystyle\frac{ V }{ T } = C_c$ |
![]() [1] "Sur la dilatation des gaz et des vapeurs", Jacques Charles, Académie des sciences française (1787)
[1] "Sur la dilatation des gaz et des vapeurs", Jacques Charles, Académie des sciences française (1787)
ID:(9529, 0)
Jacques Charles
Description 
Jacques Charles, né le 12 novembre 1746 et décédé le 7 avril 1823, était un physicien, inventeur et aéronaute français. Il est principalement connu pour son travail pionnier dans le domaine de l'aéronautique et pour ses découvertes liées au comportement des gaz. En 1783, il a effectué le premier vol habité en ballon rempli d'hydrogène, en collaboration avec le chimiste Nicolas-Louis Robert. Ce vol réussi a marqué une étape importante dans l'histoire de l'aviation. Charles a également apporté des contributions importantes à la compréhension des lois des gaz, notamment la loi de Charles, qui décrit la relation entre le volume et la température d'un gaz à pression constante.
Note : La loi de Charles a été rendue publique par Joseph Louis Gay-Lussac, qui l'a attribuée à Jacques Charles en citant un article non publié.
ID:(1656, 0)
Changement d'état d'un gaz parfait selon la loi de Charles
Concept 
La loi de Charles établit que, avec a pression ($p$) constant, le rapport de le volume ($V$) à A température absolue ($T$) est égal à A constante de la loi de Charles ($C_c$) :
| $\displaystyle\frac{ V }{ T } = C_c$ |
Cela signifie que si un gaz passe d'un état initial (le volume à l'état i ($V_i$) et a température à l'état initial ($T_i$)) à un état final (le volume à l'état f ($V_f$) et a température à l'état final ($T_f$)), en maintenant a pression ($p$) constant, il doit toujours obéir à la loi de Charles :
$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$
Ainsi, nous avons :
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
ID:(15692, 0)
Équivalent à la loi de Charles pour les densités
Concept 
Dans un processus isobare où le contenu reste constant, si le volume à l'état i ($V_i$), a température à l'état final ($T_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) sont liés par :
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Alors, nous pouvons introduire a densité ($\rho$), qui, avec a masse ($M$) et le volume ($V$), satisfait à :
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Cela nous conduit à A densité dans l'état i ($\rho_i$) et a densité dans l'état f ($\rho_f$) comme :
| $ \rho_i T_i = \rho_f T_f $ |
ID:(15693, 0)
Modèle
Top 
Paramètres
Variables
Calculs
Calculs
Calculs
Équations
$ \rho_i \equiv\displaystyle\frac{ M }{ T_i }$
rho = M / V
$ \rho_f \equiv\displaystyle\frac{ M }{ T_f }$
rho = M / V
$ \rho_i T_i = \rho_f T_f $
rho_1 * T_1 = rho_2 * T_2
$\displaystyle\frac{ V_i }{ T_i } = C_c$
V / T = C_c
$\displaystyle\frac{ V_f }{ T_f } = C_c$
V / T = C_c
$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$
V_i / T_i = V_f / T_f
ID:(15314, 0)
Loi Charles (1)
Équation 
La loi de Charles établit une relation entre le volume ($V$) et a température absolue ($T$), indiquant que leur rapport est égal à A constante de la loi de Charles ($C_c$), comme suit :
ID:(583, 1)
Loi Charles (2)
Équation 
La loi de Charles établit une relation entre le volume ($V$) et a température absolue ($T$), indiquant que leur rapport est égal à A constante de la loi de Charles ($C_c$), comme suit :
ID:(583, 2)
Changement d'état d'un gaz parfait selon la loi de Charles
Équation 
Si un gaz passe d'un état initial (i) à un état final (f) avec a pression ($p$) constant, alors pour le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) :
La loi de Charles établit que, avec a pression ($p$) constant, le rapport de le volume ($V$) à A température absolue ($T$) est égal à A constante de la loi de Charles ($C_c$) :
| $\displaystyle\frac{ V }{ T } = C_c$ |
Cela signifie que si un gaz passe d'un état initial (le volume à l'état i ($V_i$) et a température à l'état initial ($T_i$)) à un état final (le volume à l'état f ($V_f$) et a température à l'état final ($T_f$)), en maintenant a pression ($p$) constant, il doit toujours obéir à la loi de Charles :
$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$
Ainsi, nous avons :
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
ID:(3492, 0)
Masse et Densité (1)
Équation 
A densité ($\rho$) est défini comme le rapport entre a masse ($M$) et le volume ($V$), exprimé comme suit :
Cette propriété est spécifique au matériau en question.
ID:(3704, 1)
Masse et Densité (2)
Équation 
A densité ($\rho$) est défini comme le rapport entre a masse ($M$) et le volume ($V$), exprimé comme suit :
Cette propriété est spécifique au matériau en question.
ID:(3704, 2)
Équivalent à la loi de Charles pour les densités
Équation 
Pour les états initiaux (a densité dans l'état i ($\rho_i$), le volume à l'état i ($V_i$)) et finaux (a densité dans l'état f ($\rho_f$), le volume à l'état f ($V_f$)), la loi de Charles est obtenue comme suit :
Dans un processus isobare où le contenu reste constant, si le volume à l'état i ($V_i$), a température à l'état final ($T_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) sont liés par :
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Alors, nous pouvons introduire a densité ($\rho$), qui, avec a masse ($M$) et le volume ($V$), satisfait à :
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Cela nous conduit à A densité dans l'état i ($\rho_i$) et a densité dans l'état f ($\rho_f$) comme :
| $ \rho_i T_i = \rho_f T_f $ |
ID:(8835, 0)
