Ley de Charles
Storyboard 
La ley de Charles establece que el cociente entre el volumen ($V$) y la temperatura absoluta ($T$) de un gas es constante, siempre que la presión y la cantidad de moles permanezcan inalteradas.
Esto implica que el volumen ($V$) varía de forma proporcional a la temperatura absoluta ($T$).
ID:(1473, 0)
Mecanismos
Iframe 
La ley de Charles establece que el volumen de un gas es directamente proporcional a su temperatura cuando la presión se mantiene constante. Esto significa que, a medida que la temperatura de un gas aumenta, su volumen también aumenta, siempre que la presión permanezca igual. De manera inversa, si la temperatura disminuye, el volumen disminuye. Esta relación es fundamental para entender el comportamiento de los gases y se observa comúnmente al calentar o enfriar un gas en un contenedor flexible, como un globo, donde el cambio de temperatura resulta en un cambio notable de volumen.
Mecanismos
ID:(15255, 0)
Variación del volumen y temperatura
Concepto 
La generación de la presión ($p$) ocurre cuando las partículas de gas chocan con la superficie del contenedor de gas. Cada choque transmite un momento igual al doble de la masa de la partícula ($m$) por la velocidad media de una partícula ($\bar{v}$). Además, es importante considerar el flujo de partículas hacia la superficie, que depende de la concentración de particulas ($c_n$) pero también de la velocidad media de una partícula ($\bar{v}$) con el que se desplazan. Por lo tanto,
$p \propto c_n v \cdot m v = c_n m v^2$
El flujo de partículas y la transmisión del momento se representan en la siguiente gráfica:

Dado que la masa de la partícula ($m$) por la velocidad media de una partícula ($\bar{v}$) al cuadrado es proporcional a la energía, y esta a la temperatura absoluta ($T$),
$mv^2 \propto E \propto T$
y, dado que el número de partículas ($N$) es constante, la concentración de particulas ($c_n$) es inversamente proporcional a el volumen ($V$):
$c_n \propto \displaystyle\frac{1}{V}$
Dado que la presión ($p$) es constante, tenemos:
$p \propto \displaystyle\frac{T}{V}$
lo que implica:
$V \propto T$
ID:(15689, 0)
Significado de la Temperatura Absoluta
Descripción 
La temperatura corresponde a la cantidad de energía térmica (movimiento molecular) contenida en un cuerpo.
Dado que la energía siempre es positiva, escalas de temperatura como Celsius y Fahrenheit, que pueden tomar valores negativos, pueden parecer poco intuitivas. Sin embargo, la relación entre energía y temperatura lleva a la conclusión de que debe existir una temperatura mínima, conocida como temperatura cero absoluta, en la cual la energía de un sistema de partículas es nula.
Además, en 1802, Gay-Lussac observó que en los gases existe una relación proporcional entre el volumen y la temperatura. Esta proporcionalidad implica que un gas alcanzaría un volumen nulo a una temperatura de -273.15 grados Celsius (según mediciones actuales), lo que se conoce como cero absoluto de temperatura:
Esto implica que existe una escala de temperatura absoluta, conocida como la escala de grados Kelvin. Otras escalas, como las temperaturas $t$ en grados Celsius o Fahrenheit, pueden convertirse a
Celsius:
$T = 273.15 + t$
Fahrenheit:
$T = 255.37 + \displaystyle\frac{5}{9} t$
ID:(111, 0)
Igualdad de diferencias temperatura Celcius y Kelvin
Concepto 
La diferencia de temperatura en grados Celsius ($\Delta t$) en combinación con la temperatura en grados Celsius en estado 1 ($t_1$) y la temperatura en grados Celsius en estado 2 ($t_2$) da como resultado:
$\Delta t = t_2 - t_1$
Si representamos ambas temperaturas en grados Kelvin, obtenemos que la temperatura en estado 1 ($T_1$) es igual a:
$T_1 = t_1 + 273.15 , \text{K}$
y la temperatura en estado 2 ($T_2$) es igual a:
$T_2 = t_2 + 273.15 , \text{K}$
Por lo tanto, la diferencia de temperaturas en grados Kelvin, denotada como la diferencia de temperatura ($\Delta T$), se calcula como:
$\Delta T=T_2-T_1=t_2-t_1=\Delta t$
Esto implica que:
| $ \Delta T = \Delta t $ |
Lo cual significa que la diferencia entre las temperaturas en grados Celsius y Kelvin es constante.
ID:(15694, 0)
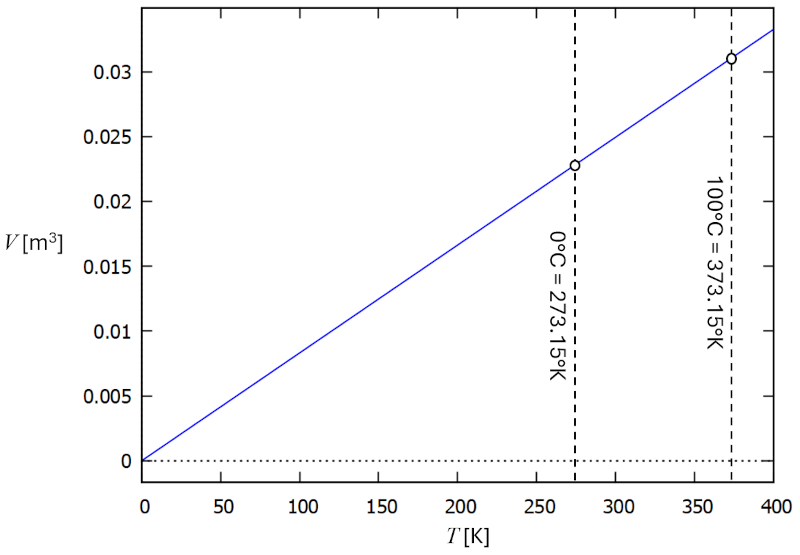
Relación temperatura vs volumen
Descripción 
En un gas, si se mantiene constante la presión ($p$) y el número de partículas ($N$), se observa que el volumen ($V$) y la temperatura absoluta ($T$) varían de forma proporcional. Cuando el volumen ($V$) disminuye, la temperatura absoluta ($T$) también disminuye, y viceversa,
$V \propto T$
como se ilustra en el siguiente gráfico:

La ley de Charles [1] establece que, manteniendo la presión ($p$) y el número de partículas ($N$) constantes, el volumen ($V$) y la temperatura absoluta ($T$) son directamente proporcionales.
Esto se puede expresar con la constante de la ley de Charles ($C_c$) de la siguiente manera:
| $\displaystyle\frac{ V }{ T } = C_c$ |
![]() [1] "Sur la dilatación de los gases y vapores" (Sobre la expansión de gases y vapores), Jacques Charles, Academia de Ciencias de Francia (1787)
[1] "Sur la dilatación de los gases y vapores" (Sobre la expansión de gases y vapores), Jacques Charles, Academia de Ciencias de Francia (1787)
ID:(9529, 0)
Jacques Charles
Descripción 
Jacques Charles, nacido el 12 de noviembre de 1746 y fallecido el 7 de abril de 1823, fue un físico, inventor y aeronauta francés. Es conocido principalmente por su trabajo pionero en el campo de la aeronáutica y por sus descubrimientos relacionados con el comportamiento de los gases. En 1783, realizó el primer vuelo tripulado en globo lleno de hidrógeno, junto con el químico Nicolas-Louis Robert. Este exitoso vuelo marcó un hito importante en la historia de la aviación. Charles también realizó importantes contribuciones en la comprensión de las leyes de los gases, incluida la Ley de Charles, que describe la relación entre el volumen y la temperatura de un gas a presión constante.
Nota: La ley de Charles se hizo pública por Joseph Louis Gay-Lussac, quien se la atribuyó a Jacques Charles citando un artículo no publicado.

Jacques Charles (1746-1823)
ID:(1656, 0)
Cambio de estado de un gas ideal según la ley de Charles
Concepto 
La ley de Charles establece que, con la presión ($p$) constante, se cumple que la proporción de el volumen ($V$) con la temperatura absoluta ($T$) es igual a la constante de la ley de Charles ($C_c$):
| $\displaystyle\frac{ V }{ T } = C_c$ |
Esto significa que si un gas pasa de un estado inicial (el volumen en estado i ($V_i$) y la temperatura en estado inicial ($T_i$)) a un estado final (el volumen en estado f ($V_f$) y la temperatura en estado final ($T_f$)), manteniendo la presión ($p$) constante, debe siempre cumplir la ley de Charles:
$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$
Por lo tanto, se tiene que:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
ID:(15692, 0)
Equivalente a la ley de Charles para densidades
Concepto 
En un proceso isobárico en el que el contenido permanece constante, si el volumen en estado i ($V_i$), la temperatura en estado final ($T_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$) están relacionados por:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Entonces, podemos introducir la densidad ($\rho$), que, junto con la masa ($M$) y el volumen ($V$), satisface:
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Esto nos lleva a la densidad en estado i ($\rho_i$) y la densidad en estado f ($\rho_f$) como:
| $ \rho_i T_i = \rho_f T_f $ |
ID:(15693, 0)
Modelo
Top 
Parámetros
Variables
Cálculos
Cálculos
Cálculos
Ecuaciones
$ \rho_i \equiv\displaystyle\frac{ M }{ T_i }$
rho = M / V
$ \rho_f \equiv\displaystyle\frac{ M }{ T_f }$
rho = M / V
$ \rho_i T_i = \rho_f T_f $
rho_1 * T_1 = rho_2 * T_2
$\displaystyle\frac{ V_i }{ T_i } = C_c$
V / T = C_c
$\displaystyle\frac{ V_f }{ T_f } = C_c$
V / T = C_c
$\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$
V_i / T_i = V_f / T_f
ID:(15314, 0)
Ley de Charles (1)
Ecuación 
La ley de Charles establece una relación entre el volumen ($V$) y la temperatura absoluta ($T$), indicando que su proporcion es igual a la constante de la ley de Charles ($C_c$), de la siguiente manera:
ID:(583, 1)
Ley de Charles (2)
Ecuación 
La ley de Charles establece una relación entre el volumen ($V$) y la temperatura absoluta ($T$), indicando que su proporcion es igual a la constante de la ley de Charles ($C_c$), de la siguiente manera:
ID:(583, 2)
Cambio de estado de un gas ideal según la ley de Charles
Ecuación 
Si un gas pasa de un estado inicial (i) a un estado final (f) con la presión ($p$) constante, se cumple que para el volumen en estado i ($V_i$), el volumen en estado f ($V_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$):
La ley de Charles establece que, con la presión ($p$) constante, se cumple que la proporción de el volumen ($V$) con la temperatura absoluta ($T$) es igual a la constante de la ley de Charles ($C_c$):
| $\displaystyle\frac{ V }{ T } = C_c$ |
Esto significa que si un gas pasa de un estado inicial (el volumen en estado i ($V_i$) y la temperatura en estado inicial ($T_i$)) a un estado final (el volumen en estado f ($V_f$) y la temperatura en estado final ($T_f$)), manteniendo la presión ($p$) constante, debe siempre cumplir la ley de Charles:
$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$
Por lo tanto, se tiene que:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
ID:(3492, 0)
Masa y Densidad (1)
Ecuación 
La densidad ($\rho$) se define como la relación entre la masa ($M$) y el volumen ($V$), que se expresa como:
Esta propiedad es específica del material en cuestión.
ID:(3704, 1)
Masa y Densidad (2)
Ecuación 
La densidad ($\rho$) se define como la relación entre la masa ($M$) y el volumen ($V$), que se expresa como:
Esta propiedad es específica del material en cuestión.
ID:(3704, 2)
Equivalente a la ley de Charles para densidades
Ecuación 
Para los estados inicial (la densidad en estado i ($\rho_i$), el volumen en estado i ($V_i$)) y final (la densidad en estado f ($\rho_f$), el volumen en estado f ($V_f$)), la ley de Charles se obtiene como sigue:
En un proceso isobárico en el que el contenido permanece constante, si el volumen en estado i ($V_i$), la temperatura en estado final ($T_f$), la temperatura en estado inicial ($T_i$) y la temperatura en estado final ($T_f$) están relacionados por:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Entonces, podemos introducir la densidad ($\rho$), que, junto con la masa ($M$) y el volumen ($V$), satisface:
| $ \rho \equiv\displaystyle\frac{ M }{ V }$ |
Esto nos lleva a la densidad en estado i ($\rho_i$) y la densidad en estado f ($\rho_f$) como:
| $ \rho_i T_i = \rho_f T_f $ |
ID:(8835, 0)
