Utilizador:
Força viscosa e gravitação
Storyboard 
Quando um corpo se move em um meio viscoso sob a influência de uma força constante, como a gravidade, inicialmente a gravidade acelera o corpo até que sua velocidade aumente a um nível onde a força viscosa e a gravidade se equilibram. A partir desse ponto em diante, o corpo não sofre mais aceleração e se move a uma velocidade constante.
ID:(1965, 0)
Mecanismos
Iframe
Mecanismos
ID:(15539, 0)
Força viscosa sobre um corpo
Top
A força experimentada por um corpo que se desloca com uma velocidade de ($$) em um meio, caracterizado por la constante de força viscosa ($b$), é La força viscosa ($F_v$), como descrito pela equação:
| $ F_v = b v $ |
Para entender o papel de la constante de força viscosa ($b$), é importante lembrar que a viscosidade é uma medida de como o momento, ou a velocidade das moléculas, se difunde. Em outras palavras, la constante de força viscosa ($b$) é a medida pela qual o corpo perde energia ao transferi-la para o meio e ao acelerar as moléculas, fornecendo-lhes energia. Portanto, la constante de força viscosa ($b$) é proporcional à viscosidade.
ID:(15546, 0)
Forças sobre uma esfera caindo em um meio
Descrição
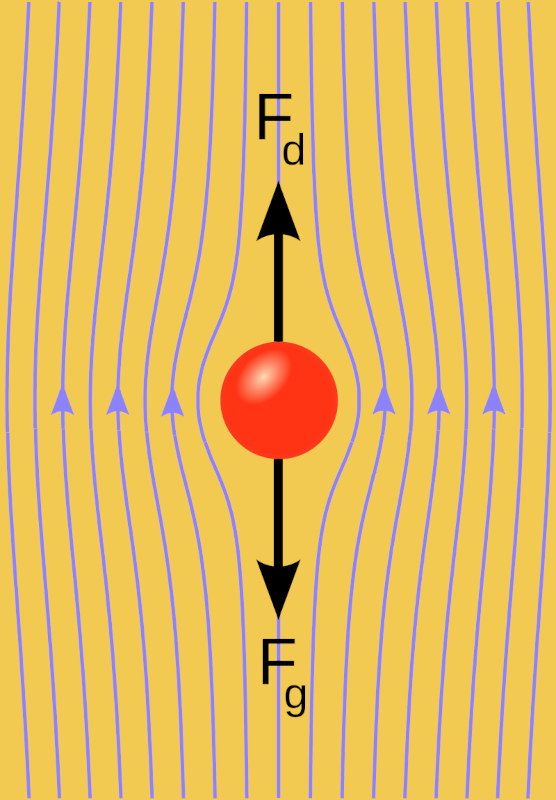
Quando uma esfera é lançada em um meio viscoso, surge uma força inicial ascendente, uma força gravitacional ($F_g$), que afunda gradualmente o corpo. Durante esse processo, a esfera ganha velocidade, resultando em uma força descendente, uma força viscosa ($F_v$), que depende da velocidade. Conforme a velocidade total, la força com massa constante ($F$),
| $ F = F_g - F_v $ |
começa a diminuir até se tornar nula. A partir desse momento, o movimento continua com velocidade constante, já que não há força para acelerá-lo.
ID:(15544, 0)
Método Ostwald para medir a viscosidade
Descrição
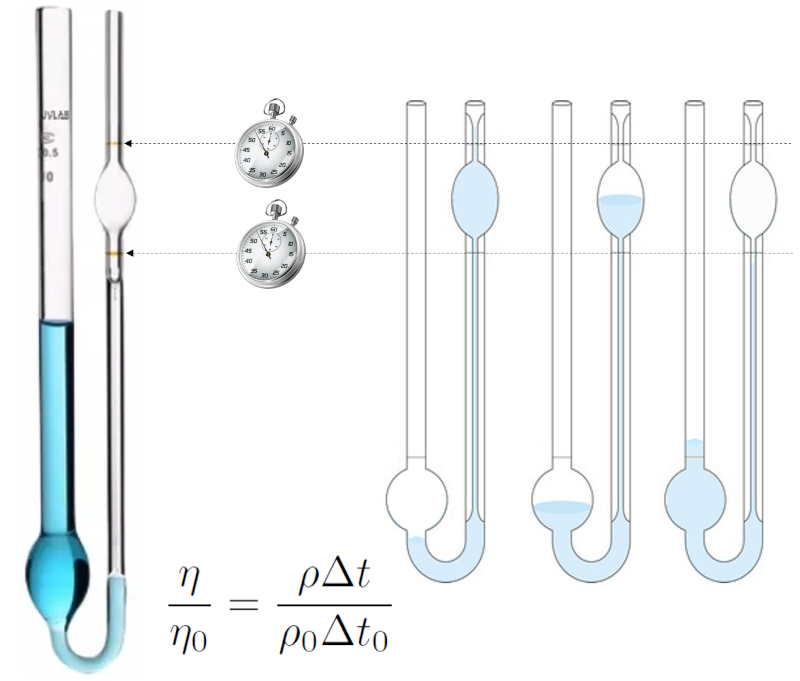
O método de medição de viscosidade de Ostwald baseia-se no comportamento de um líquido fluindo através de um tubo de pequeno raio (capilar).
O líquido é introduzido, aplica-se sucção para exceder a marca superior e, em seguida, permite-se que escorra, medindo o tempo que leva para o nível passar da marca superior para a inferior.
O experimento é conduzido primeiro com um líquido para o qual a viscosidade e a densidade são conhecidas (por exemplo, água destilada), e depois com o líquido para o qual se deseja determinar a viscosidade. Se as condições forem idênticas, o líquido fluindo em ambos os casos será semelhante e, assim, o tempo será proporcional à densidade dividida pela viscosidade. Portanto, pode-se estabelecer uma equação de comparação entre ambas as viscosidades:
ID:(15545, 0)
Velocidade de queda em meio viscoso
Top
No caso de um corpo caindo em um meio viscoso, a equação de movimento é uma equação de la velocidade ($v$) em função de o tempo ($t$) com la massa gravitacional ($m_g$), la massa inercial ($m_i$), la aceleração gravitacional ($g$) e la constante de força viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Isso é obtido com la tempo de viscosidade e massa inercial ($\tau_i$)
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
e com la tempo de viscosidade e massa gravitacional ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
Integrando com tempo inicial zero e la velocidade inicial ($v_0$),
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
que é representado abaixo:
O gráfico ilustra como a viscosidade força o corpo a descer com uma velocidade assintótica ($v_{\infty}$), o que equivale a $g\tau_g$. Isso ocorre em um tempo da ordem de la tempo de viscosidade e massa inercial ($\tau_i$), seja quando la velocidade ($v$) é menor ou maior que la velocidade assintótica ($v_{\infty}$).
ID:(15547, 0)
Trajetória de queda em meio viscoso
Top
No caso de um corpo caindo em um meio viscoso, a equação de movimento é uma equação de la posição ($s$) em função de la aceleração gravitacional ($g$), la tempo de viscosidade e massa inercial ($\tau_i$), la tempo de viscosidade e massa gravitacional ($\tau_g$), la velocidade inicial ($v_0$) e o tempo ($t$):
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
A partir desta equação, obtemos integrando com tempo inicial zero e uma velocidade ($s_0$):
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
que é representada abaixo:
ID:(15550, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$
@DIFF( s , t )= g * tau_g + ( v_0 - g * tau_g )*exp(- t / tau_i )
$ F = F_g - F_v $
F = F_g - F_v
$ F = m_i a $
F = m_i * a
$ F_g = m_g g $
F_g = m_g * g
$ F_v = b v $
F_v = b * v
$ m_g = m_i $
m_g = m_i
$ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $
m_i * @DIFF( v , t ) = m_g * g - b * v
$ m_i a = m_g g - b v $
m_i * a = m_g * g - b * v
$ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$
s = s_0 + g * tau_g * t + ( v_0 - g * tau_g )* tau_i *(1-exp(- t / tau_i ))
$ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$
tau_g = m_g / b
$ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$
tau_i = m_i / b
$ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$
v = g * tau_g + ( v_0 - g * tau_g )*exp(- t / tau_i )
$ v_{\infty} \equiv g \tau_g $
v_i = g * tau_g
ID:(15541, 0)
Força total do corpo caindo em meio viscoso
Equação
No caso de um corpo que cai em um meio viscoso, a força total, la força com massa constante ($F$), é igual a la força gravitacional ($F_g$) menos la força viscosa ($F_v$), então
| $ F = F_g - F_v $ |
ID:(15543, 0)
Caso de força massa constante
Equação
No caso em que la massa inercial ($m_i$) é igual a la massa inicial ($m_0$),
| $ m_g = m_i $ |
a derivada do momento será igual à massa multiplicada pela derivada de la velocidade ($v$). Dado que a derivada da velocidade é La aceleração instantânea ($a$), temos que la força com massa constante ($F$) é igual a
| $ F = m_i a $ |
Dado que o momento ($p$) se define con la massa inercial ($m_i$) y la velocidade ($v$),
| $ p = m_i v $ |
Si la massa inercial ($m_i$) é igual a la massa inicial ($m_0$), então podemos derivar o momento em relação ao tempo e obter la força com massa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Portanto, chegamos à conclusão de que
| $ F = m_i a $ |
ID:(10975, 0)
Força viscosa
Equação
A forma mais simples de la força viscosa ($F_v$) é aquela que é proporcional ao la velocidade ($v$) do corpo, representada por:
| $ F_v = b v $ |
A constante de proporcionalidade, também conhecida como la constante de força viscosa ($b$), geralmente depende da forma do objeto e da viscosidade do meio através do qual ele se move. Um exemplo desse tipo de força é aquela exercida por um fluxo de fluido em um corpo esférico, cuja expressão matemática é conhecida como a lei de Stokes.
ID:(3243, 0)
Força gravitacional
Equação
La força gravitacional ($F_g$) baseia-se em la massa gravitacional ($m_g$) do objeto e em uma constante que reflete a intensidade da gravidade na superfície do planeta. Esta última é identificada por la aceleração gravitacional ($g$), que é igual a $9.8 m/s^2$.
Consequentemente, conclui-se que:
| $ F_g = m_g g $ |
ID:(3241, 0)
Igualdade das massas inercial e gravitacional
Equação
As massas que Newton utilizou em seus princípios estão relacionadas à inércia dos corpos, o que leva ao conceito de la massa inercial ($m_i$).
A lei de Newton, que está ligada à força entre corpos devido às suas massas, está relacionada à gravidade, sendo conhecida como la massa gravitacional ($m_g$).
Empiricamente, concluiu-se que ambas as massas são equivalentes, e, portanto, definimos
| $ m_g = m_i $ |
Einstein foi quem questionou essa igualdade e, a partir dessa dúvida, compreendeu por que ambas 'aparecem' iguais em sua teoria da gravidade. Em seu argumento, Einstein explicou que as massas deformam o espaço, e essa deformação do espaço causa uma mudança no comportamento dos corpos. Assim, as massas acabam sendo equivalentes. O conceito revolucionário da curvatura do espaço implica que até mesmo a luz, que não tem massa, é afetada por corpos celestes, contradizendo a teoria da gravitação de Newton. Isso foi demonstrado experimentalmente ao estudar o comportamento da luz durante um eclipse solar. Nessa situação, os feixes de luz são desviados devido à presença do sol, permitindo a observação de estrelas que estão atrás dele.
ID:(12552, 0)
Equação do movimento caindo em um meio viscoso
Equação
La força com massa constante ($F$) é igual a la força gravitacional ($F_g$) menos la força viscosa ($F_v$), então:
| $ F = F_g - F_v $ |
Essa relação permite estabelecer a equação de movimento para la aceleração instantânea ($a$) com uma massa inercial ($m_i$) caindo devido à gravidade da Terra com la aceleração gravitacional ($g$), e com uma massa gravitacional ($m_g$), em la constante de força viscosa ($b$), assumirá a forma de:
| $ m_i a = m_g g - b v $ |
ID:(14495, 0)
Equação diferencial para queda em meio viscoso
Equação
La massa inercial ($m_i$) que cai devido à gravidade da Terra com uma aceleração gravitacional ($g$), e com uma massa gravitacional ($m_g$) em um meio viscoso com uma constante de força viscosa ($b$), é apresentado da seguinte forma:
| $ m_i a = m_g g - b v $ |
Para resolver esta equação, é necessário levá-la à sua forma diferencial. Isso é alcançado substituindo la aceleração instantânea ($a$) pela derivada de la velocidade ($v$) em o tempo ($t$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
ID:(14492, 0)
Tempo de massa gravitacional e viscosidade
Equação
Com a equação de movimento de um corpo em um meio viscoso, temos a derivada de la velocidade ($v$) em o tempo ($t$) com la massa inercial ($m_i$), la massa gravitacional ($m_g$), la constante de força viscosa ($b$) e la aceleração gravitacional ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Isso define la tempo de viscosidade e massa gravitacional ($\tau_g$) como:
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
ID:(15549, 0)
Tempo de massa inercial e viscosidade
Equação
Com a equação de movimento de um corpo em um meio viscoso, temos a derivada de la velocidade ($v$) em o tempo ($t$) com la constante de força viscosa ($b$) e la aceleração gravitacional ($g$):
| $ m_i \displaystyle\frac{dv}{dt} = - b v $ |
Isso define la tempo de viscosidade e massa inercial ($\tau_i$) como:
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
ID:(15548, 0)
Solução do movimento caindo em um meio viscoso
Equação
A equação do movimento em la velocidade ($v$) em o tempo ($t$) com la massa inercial ($m_i$), la massa gravitacional ($m_g$), la aceleração gravitacional ($g$) e la constante de força viscosa ($b$) é:
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
Supondo que o tempo inicial seja zero, la velocidade inicial ($v_0$), la tempo de viscosidade e massa gravitacional ($\tau_g$) e la tempo de viscosidade e massa inercial ($\tau_i$), obtemos a seguinte equação:
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
A equação de movimento em la velocidade ($v$) em o tempo ($t$) com la massa inercial ($m_i$), la massa gravitacional ($m_g$), la aceleração gravitacional ($g$) e la constante de força viscosa ($b$):
| $ m_i \displaystyle\frac{dv}{dt} = m_g g - b v $ |
juntamente com a definição de la tempo de viscosidade e massa inercial ($\tau_i$)
| $ \tau_i \equiv \displaystyle\frac{ m_i }{ b }$ |
e la tempo de viscosidade e massa gravitacional ($\tau_g$)
| $ \tau_g \equiv \displaystyle\frac{ m_g }{ b }$ |
pode ser reformulada como
$\displaystyle\frac{dv}{g\tau_g - v} = \displaystyle\frac{dt}{\tau_i}$
Se integrarmos essa expressão entre uma velocidade inicial ($v_0$) e la velocidade ($v$), e do tempo inicial zero até O tempo ($t$), obtemos
$\ln(g\tau_g-v_0)-\ln(g\tau_g-v)=\displaystyle\frac{t}{\tau_i}$
Resolvendo para a velocidade, obtemos
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
Esta equação ilustra que la velocidade inicial ($v_0$) então converge assintoticamente para a velocidade $g\tau_g$.
ID:(14493, 0)
Velocidade assintótica
Equação
A integração da equação do movimento resulta em la velocidade ($v$) como uma função de la aceleração gravitacional ($g$), la tempo de viscosidade e massa inercial ($\tau_i$), la tempo de viscosidade e massa gravitacional ($\tau_g$), la velocidade inicial ($v_0$) e o tempo ($t$) da seguinte forma:
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
Para o tempo ($t$) muito maior que la tempo de viscosidade e massa inercial ($\tau_i$), obtém-se o limite la velocidade assintótica ($v_{\infty}$):
| $ v_{\infty} \equiv g \tau_g $ |
ID:(14494, 0)
Equação diferencial trajetória de queda em meio viscoso
Equação
A integração da equação do movimento resulta em la velocidade ($v$) como uma função de la aceleração gravitacional ($g$), la tempo de viscosidade e massa inercial ($\tau_i$), la tempo de viscosidade e massa gravitacional ($\tau_g$), la velocidade inicial ($v_0$) e o tempo ($t$) da seguinte forma:
| $ v = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
em sua forma diferencial,
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
onde la posição ($s$) representa a distância percorrida.
ID:(14496, 0)
Caminho em uma queda em meio viscoso
Equação
A integração da equação de movimento produz la posição ($s$) em termos de la aceleração gravitacional ($g$), la tempo de viscosidade e massa inercial ($\tau_i$), la tempo de viscosidade e massa gravitacional ($\tau_g$), la velocidade inicial ($v_0$) e o tempo ($t$) da seguinte forma:
| $ \displaystyle\frac{ds}{dt} = g \tau_g + ( v_0 - g \tau_g )e^{- t / \tau_i }$ |
do tempo inicial nulo até O tempo ($t$), e de la velocidade ($s_0$) até La posição ($s$), obtemos
| $ s = s_0 + g \tau_g t +( v_0 - g \tau_g ) \tau_i (1 - e^{- t / \tau_i })$ |
ID:(14497, 0)