Utilizador:
Força de uma mola
Storyboard 
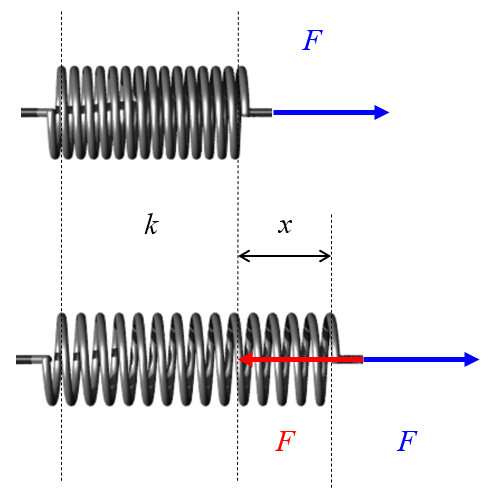
A força gerada por uma mola é diretamente proporcional à sua elongação.
A constante de proporcionalidade é chamada de constante da mola ou constante de Hooke. Da mesma forma, a relação dessa força é chamada de Lei de Hooke.
ID:(1414, 0)
Mecanismos
Iframe
Mecanismos
ID:(15521, 0)
Lei de Hooke
Imagem
Se a força necessária para alcançar uma determinada elongação na mola for medida, perceberá que ambas são proporcionais:
A mola é pendurada verticalmente e pesos conhecidos são adicionados a ela. A elongação resultante é medida e um gráfico de força versus elongação é traçado. A inclinação dessa relação, conhecida como constante elástica da mola ou constante de Hooke, depende das propriedades da mola.
A linearidade dessa relação permite o uso de molas como um método para medir forças.
A força pode ser medida usando uma mola, estabelecendo uma escala proporcional à elongação que indica diretamente a força associada.
O instrumento usado para medir forças usando uma mola é chamado de dinamômetro (a 'dina' é a unidade de força no sistema cgs - centímetros, gramas, segundos - de modo que 10^5 dinas equivalem a um Newton).
ID:(11530, 0)
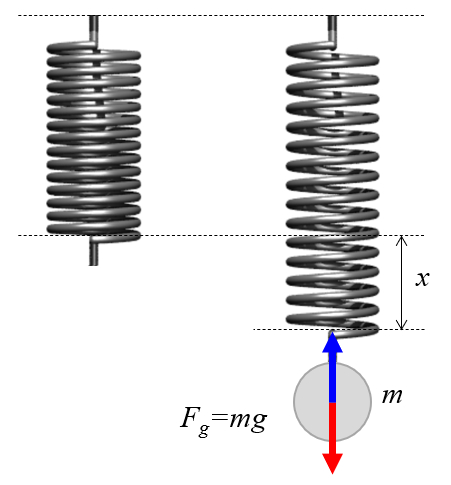
Estudo do comportamento da mola
Imagem
Para estudar como a mola se alonga, ela pode ser suspensa verticalmente e gradualmente carregada com pesos conhecidos.
ID:(12528, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ F = F_k - F_g $
F = F_k - F_g
$ F = m_i a $
F = m_i * a
$ F_g = m_g g $
F_g = m_g * g
$ F_k = k x $
F_k = k * u
$ m_g = m_i $
m_g = m_i
$ m_i a = k x - m_g g $
m_i * a = k * x - m_g * g
$ \nu =\displaystyle\frac{1}{ T }$
nu =1/ T
$ \omega = 2 \pi \nu $
omega = 2* pi * nu
$ \omega = \displaystyle\frac{2 \pi }{ T }$
omega = 2* pi / T
$ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$
omega_0 ^2 = k / m_i
$ v = - x_0 \omega \sin \omega t + v_0 \cos \omega t $
v = - x_0 * omega_0 *sin( omega_0 * t )+ v_0 *cos( omega_0 * t )
$ x = x_0 \cos \omega t + \displaystyle\frac{ v_0 }{ \omega }\sin \omega t + \displaystyle\frac{ g }{ \omega ^2}$
x = x_0 *cos( omega_0 * t )+ v_0 *sin( omega_0 * t )/ omega_0 + g / omega_0 ^2
ID:(15533, 0)
Equilíbrio das forças da mola e gravitacionais
Equação
A equação do movimento é estabelecida com o equilíbrio de forças, o que significa que la força com massa constante ($F$) é igual a la força elástica ($F_k$) menos la força gravitacional ($F_g$):
| $ F = F_k - F_g $ |
ID:(15560, 0)
Caso de força massa constante
Equação
No caso em que la massa inercial ($m_i$) é igual a la massa inicial ($m_0$),
| $ m_g = m_i $ |
a derivada do momento será igual à massa multiplicada pela derivada de la velocidade ($v$). Dado que a derivada da velocidade é La aceleração instantânea ($a$), temos que la força com massa constante ($F$) é igual a
| $ F = m_i a $ |
Dado que o momento ($p$) se define con la massa inercial ($m_i$) y la velocidade ($v$),
| $ p = m_i v $ |
Si la massa inercial ($m_i$) é igual a la massa inicial ($m_0$), então podemos derivar o momento em relação ao tempo e obter la força com massa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Portanto, chegamos à conclusão de que
| $ F = m_i a $ |
ID:(10975, 0)
Lei de Hooke
Equação
A relação entre la força elástica ($F_k$) e a elongação la alongamento ($u$) é escrita e conhecida como Lei de Hooke. A constante la constante de Hooke ($k$) é chamada de constante elástica da mola:
| $ F_k = k x $ |
| $ F_k = k u $ |
ID:(3207, 0)
Força gravitacional
Equação
La força gravitacional ($F_g$) baseia-se em la massa gravitacional ($m_g$) do objeto e em uma constante que reflete a intensidade da gravidade na superfície do planeta. Esta última é identificada por la aceleração gravitacional ($g$), que é igual a $9.8 m/s^2$.
Consequentemente, conclui-se que:
| $ F_g = m_g g $ |
ID:(3241, 0)
Equação de movimento da mola
Equação
A equação do movimento é obtida diretamente da equação das forças, onde la força com massa constante ($F$) é igual a la força elástica ($F_k$) menos la força gravitacional ($F_g$):
| $ F = F_k - F_g $ |
Esta equação é expressa em relação às diferentes forças envolvidas, incluindo la aceleração instantânea ($a$), la alongamento de mola ($x$), la constante de Hooke ($k$), la massa inercial ($m_i$), la massa gravitacional ($m_g$) e la aceleração gravitacional ($g$), da seguinte forma:
| $ m_i a = k x - m_g g $ |
Como la força com massa constante ($F$) é igual a la força elástica ($F_k$) menos la força gravitacional ($F_g$):
| $ F = F_k - F_g $ |
Se considerarmos que la força com massa constante ($F$) com la massa inercial ($m_i$) e la aceleração instantânea ($a$) é
| $ F = m_i a $ |
e que la força elástica ($F_k$) é com la constante de Hooke ($k$) e la alongamento ($u$) é
| $ F_k = k x $ |
e que la força gravitacional ($F_g$) é com la massa gravitacional ($m_g$) e la aceleração gravitacional ($g$)
| $ F_g = m_g g $ |
então resulta
| $ m_i a = k x - m_g g $ |
ID:(11293, 0)
Igualdade das massas inercial e gravitacional
Equação
As massas que Newton utilizou em seus princípios estão relacionadas à inércia dos corpos, o que leva ao conceito de la massa inercial ($m_i$).
A lei de Newton, que está ligada à força entre corpos devido às suas massas, está relacionada à gravidade, sendo conhecida como la massa gravitacional ($m_g$).
Empiricamente, concluiu-se que ambas as massas são equivalentes, e, portanto, definimos
| $ m_g = m_i $ |
Einstein foi quem questionou essa igualdade e, a partir dessa dúvida, compreendeu por que ambas 'aparecem' iguais em sua teoria da gravidade. Em seu argumento, Einstein explicou que as massas deformam o espaço, e essa deformação do espaço causa uma mudança no comportamento dos corpos. Assim, as massas acabam sendo equivalentes. O conceito revolucionário da curvatura do espaço implica que até mesmo a luz, que não tem massa, é afetada por corpos celestes, contradizendo a teoria da gravitação de Newton. Isso foi demonstrado experimentalmente ao estudar o comportamento da luz durante um eclipse solar. Nessa situação, os feixes de luz são desviados devido à presença do sol, permitindo a observação de estrelas que estão atrás dele.
ID:(12552, 0)
Oscilações com mola
Equação
O produto de la constante de Hooke ($k$) e la massa inercial ($m_i$) é denominado la frequência angular da mola ($\omega$) e é definido como:
| $ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$ |
ID:(1242, 0)
Frequência angular
Equação
La frequência angular ($\omega$) é com la período ($T$) igual a
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
ID:(12335, 0)
Frequência
Equação
La frequência ($\nu$) corresponde ao número de vezes que ocorre uma oscilação em um segundo. Já La período ($T$) é o tempo que uma única oscilação leva. Portanto, o número de oscilações por segundo é:
| $ \nu =\displaystyle\frac{1}{ T }$ |
A frequência é indicada em Hertz (Hz).
ID:(4427, 0)
Solução para posição
Equação
A variável la amplitude de oscilação ($x$) evolui em relação a o tempo ($t$) de acordo com a equação de movimento com la frequência angular do oscilador ($\omega_0$) e la aceleração gravitacional ($g$) dada por:
| $\displaystyle\frac{d v }{d t } = \displaystyle\frac{ k x }{ m_i }- g $ |
Se assumirmos que la amplitude inicial da oscilação ($x_0$) e la velocidade inicial do oscilador ($v_0$) são a solução, podemos escrever:
| $ x = x_0 \cos \omega t + \displaystyle\frac{ v_0 }{ \omega }\sin \omega t + \displaystyle\frac{ g }{ \omega ^2}$ |
| $ x = x_0 \cos \omega_0 t + \displaystyle\frac{ v_0 }{ \omega_0 }\sin \omega_0 t + \displaystyle\frac{ g }{ \omega_0 ^2}$ |
ID:(15564, 0)
Solução para velocidade
Equação
Para obter la velocidade do oscilador ($v$), basta derivar la amplitude de oscilação ($x$) em relação a o tempo ($t$):
| $ v =\displaystyle\frac{ d s }{ d t }$ |
Assim, obtemos com la amplitude inicial da oscilação ($x_0$), la velocidade inicial ($v_0$) e la frequência angular do oscilador ($\omega_0$) que:
| $ v = - x_0 \omega \sin \omega t + v_0 \cos \omega t $ |
| $ v = - x_0 \omega_0 \sin \omega_0 t + v_0 \cos \omega_0 t $ |
ID:(15565, 0)